
hello大家好,淘气的我又来了,今天我给大家带来了和动态规划相关的问题,带好笔和纸,咱们开始了
一.题目描述

我们举一个简单的例子,看下边这个图
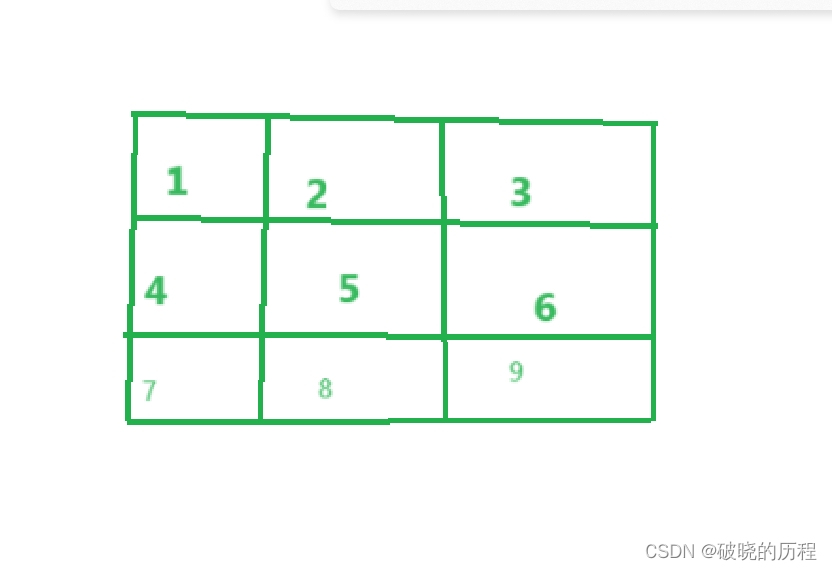
要想从1到9,我们有如下几种符合要求的选择
1.1->2->3->6->9;
2.1->2->5->6->9;
3.1->4->5->6->9;
4.1->2->5->8->9;
5.1->4->5->8->9;
6.1->4->7->8->9;
二.讲解算法原理
1.状态表示
dp[i][j]表示从出发点到[i][j]位置一共有多少中走法;
2.状态转移方程
如上图所示,我们不难发现,如果想要到达第9个格,那么首先我们必须到第8个格或者第6个格
所以

所以我们得出结论;dp[i][j]=dp[i-1][j]+dp[i][j-1];
3.初始化问题
初始化问题是这类动态规划问题必须解决的一个问题

当dp[i][j]表示如下位置时,会出现越界行为,所以,我们可以这样
由原先的m*n的数组加上一行一列,变为(m+1)*(n+1)的数组
我们知道,会出现越界的位置,都是只有一种路径
所以我们可以把新加的几个位置初始化为如下
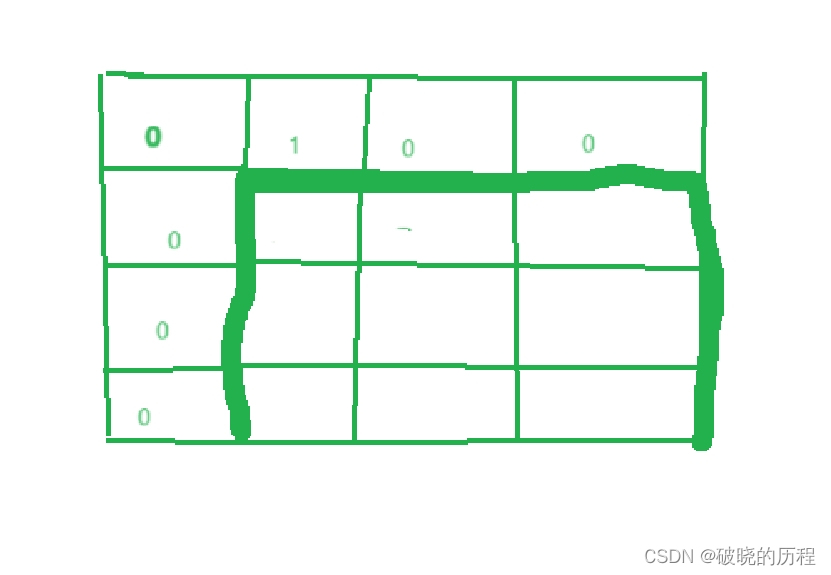
如此,根据我们的状态转移方程,可以得出可能越界的位置的路径正好为1;
4.填充顺序
我们仍然采取由上到下,从左到右的顺序
5.返回值
返回dp[m][n]的值;
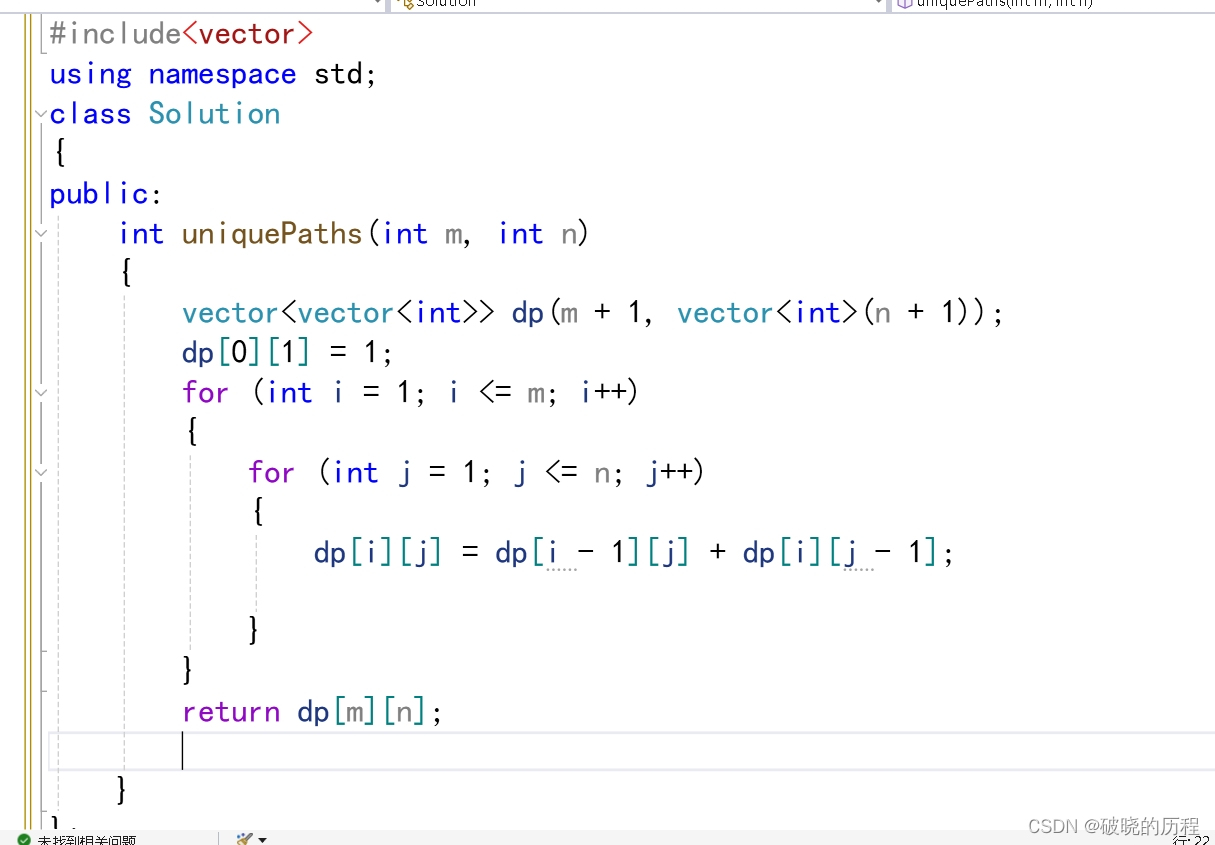
三.代码实现























 5万+
5万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








