求解0/1背包问题
问题描述:有n个重量分别为w1, w2, …, wn的物品(编号为1~n),它们的价值分别为v1, v2, …, vn,给定一个容量为W的背包。设计从这些物品中选取一部分物品装入背包的方案,每个物品要么装入要么不装入,要求选中的物品不仅能够放入背包,还要拥有最大的价值。物品信息如下表:

蛮力法
一、算法思路
采用求幂集的方法求出所有的物品组合,每种物品组合求出其sumw和sumv,sumw ≤ W时是一种解,通过比较将最佳方案保存到maxsumw和maxsumv中,最后输出。
*求解幂集问题的算法见这篇文章 *
二、代码展示
#include <iostream>
#include <vector>
using namespace std;
vector<vector<int>> find_set(int a[], int n) { //用求幂集的方法求出所有可能的情况
vector<vector<int>> ps, psl;
vector<vector<int>>::iterator ps_ite;
ps.push_back({});
for (int i = 0; i < n; i++) {
psl = ps;
for (ps_ite = psl.begin(); ps_ite != psl.end(); ps_ite++) {
(*ps_ite).push_back(a[i]);
ps.push_back(*ps_ite);
}
}
return ps;
}
//打印所有方案,并输出最佳方案
void find_best_solution(vector<vector<int>> ps, int w[], int v[], int flag[], int W) {
vector<vector<int>>::iterator ps_ite;
vector<int> s;
vector<int>::iterator s_ite;
int maxsumw = 0, maxsumv = 0, maxindex = 0;
int sumw, sumv;
cout << "0/1背包所有组合情况如下:" << endl;
int i = 1;
cout << "方案编号\t物品组合\t总重量\t总价值" << endl;
for (ps_ite = ps.begin(); ps_ite != ps.end(); ps_ite++) {
sumw = 0; sumv = 0;
cout << i << "\t{";
for (s_ite = (*ps_ite).begin(); s_ite != (*ps_ite).end(); s_ite++) {
cout << *s_ite;
sumw += w[(*s_ite) - 1];
sumv += v[(*s_ite) - 1];
}
if ((sumw <= W) && (sumv > maxsumv)) {
maxsumw = sumw;
maxsumv = sumv;
maxindex = i;
}
cout << "}\t" << sumw << "\t" << sumv << endl;
i++;
}
cout << "最佳结果如下: " << endl;
cout << "方案编号\t物品组合\t总重量\t总价值" << endl;
cout << maxindex << "\t";
i = 1;
for (ps_ite = ps.begin(); ps_ite != ps.end(); ps_ite++) {
if (i == maxindex) {
cout << "{";
for (s_ite = (*ps_ite).begin(); s_ite != (*ps_ite).end(); s_ite++) {
cout << *s_ite;
}
cout << "}\t";
break;
}
i++;
}
cout << maxsumw << "\t" << maxsumv << endl;
}
int main() {
int w[] = { 5, 3, 2, 1 };
int v[] = { 4, 4, 3, 1 };
int W = 6;
int flag[] = { 1, 2, 3, 4 };
int n = sizeof(flag) / sizeof(flag[0]);
vector<vector<int>> ps = find_set(flag, n);
find_best_solution(ps, w, v, flag, W);
return 0;
}
最终结果如下:
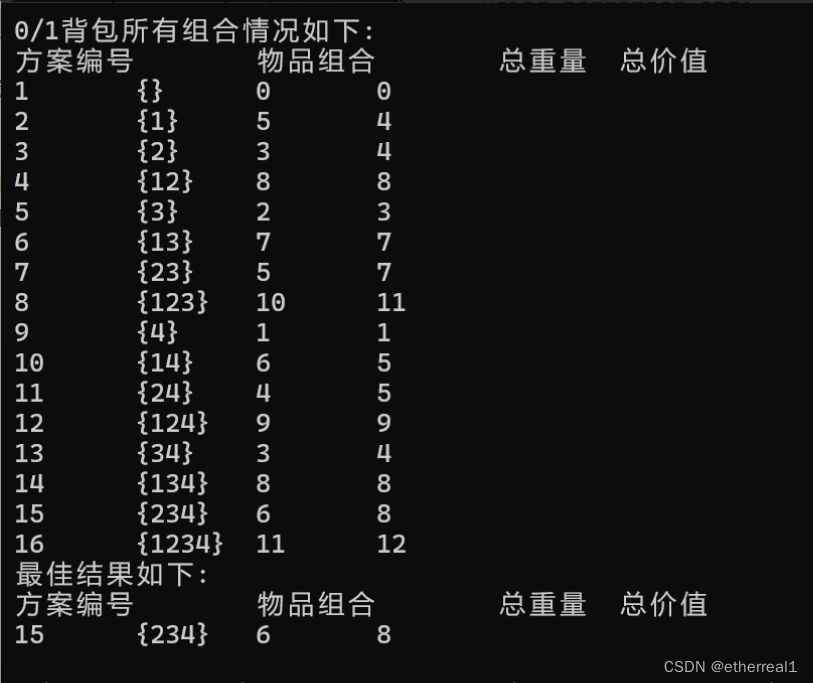
三、算法分析
对于n个物品,最主要的时间花费在求幂集上,因此时间复杂度为O(2n)
回溯法
装入背包中的物品重量和为W
一、算法思路
设n个物品的编号为0~n-1,重量用数组w[0…n-1]存放,价值用数组v[0…n-1]存放,限制重量用W表示。用x[0…n-1]数组存放最优解,x[i] = 1表示选取编号为i的物品,x[i] = 0表示不选取编号为i的物品。
由于每个物品要么装入,要么不装入,其解空间是一棵子集树,树中的每个节点表示背包的一种选择状态,记录当前放入背包物品的总重量和总价值,每个分支节点的两条边分别表示对某物品是否放入背包的两种可能的选择。
i层表示考虑编号为i的物品是否装入背包,n层表示已经考虑了所有物品,对应一个解向量。对i层上的某个分支节点,对应的状态为(i, tw, tv, op),其中:tw表示当前背包重量,tv表示当前背包价值,op对应解向量。该分支节点对应的扩展状态如下:
- op[i] = 1,表示选取物品i,下一个状态为:(i + 1, tw + w[i], tv + v[i], op),对应左分支
- op[i] = 0,表示不选物品i,下一个状态为:(i + 1, tw, tv, op),对应右分支
对n层的叶节点,通过限制条件W和比较,选出满足条件的最大价值方案,将价值存储在maxv中,将对应方案存储在数组x中。
另外,为了进一步加快算法运行时间,可以增加剪枝函数,思路如下:
- 左剪枝:对于i层的节点,如果选择物品i会导致超重,即tw + w[i] > W,就不再扩展该节点,即仅扩展tw + w[i] ≤ W的节点
- 右剪枝:用rw表示考虑物品i时剩余物品的总重量,即:rw = w[i] + … + w[n - 1],初始时rw是所有物品的重量和。对于i层上的某节点,其状态:(i, tw, tv, rw, op),对应的两种扩展如下:
(1)op[i] = 1,下一个状态为:(i + 1, tw + w[i], tv + v[i], rw - w[i], op)
(2)op[i] = 0,下一个状态为:(i + 1, tw, tv, rw - w[i], op)
显然,当不选择物品i时,tw + rw - w[i] = tw + w[i + 1] + … + w[n - 1],若该值小于W,也就是说即使选择后面的所有物品,重量也不会达到W,与题意不符,因此不扩展该节点,即:进扩展tw + rw - w[i] ≥ W的节点。
例:对于问题中的4个物品,在限制背包总重量为W=6时,求出对应解空间树如下:

其中,红色编号为节点扩展顺序
二、代码展示
#include <iostream>
using namespace std;
int w[] = { 5, 3, 2, 1 };
int v[] = { 4, 4, 3, 1 };
int W = 6;
int maxv = 0;
int x[] = { 0, 0, 0, 0 };
int n = 4;
void dfs(int i, int tw, int tv, int rw, int op[]) {
if (i == n) {
if ((tw == W) && (tv > maxv)) {
maxv = tv;
for (int i = 0; i < n; i++) {
x[i] = op[i];
}
}
}
else {
if (tw + w[i] <= W) {
op[i] = 1;
dfs(i + 1, tw + w[i], tv + v[i], rw - w[i], op);
}
if (tw + rw - w[i] >= W) {
op[i] = 0;
dfs(i + 1, tw, tv, rw - w[i], op);
}
}
}
int main() {
int sumw = 0;
for (int i = 0; i < n; i++) {
sumw += w[i];
}
int op[] = {0, 0, 0, 0};
dfs(0, 0, 0, sumw, op);
cout << "最大价值为:" << maxv << endl;
cout << "对应方案为:{";
for (int i = 0; i < n; i++) {
if (x[i] == 1) {
cout << (i + 1);
}
}
cout << "}" << endl;
return 0;
}
最终结果如下:
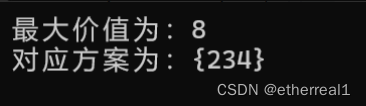
装入背包中的物品重量和不超过W
一、算法思路
由于问题改为求背包中物品重量和不超过W的最大价值的装入方案,前面左剪枝方式不变,但右剪枝方式不再有效,改为采用上界函数进行右剪枝。
对于i层的某个分支节点,状态为(i, tw, tv, op),若不选择物品i,设置对应的上界函数bound(i) = tv + r,表示沿着该方向选择物品的价值上限,其中r表示剩余物品的总价值。假设当前求出的最大价值为maxv,若bound(i) ≤ maxv,则右剪枝,否则继续扩展。显然r越小,bound(i)也越小,剪枝越多,为了构造更小的r,将所有物品以单位重量价值递减排列。如下图:
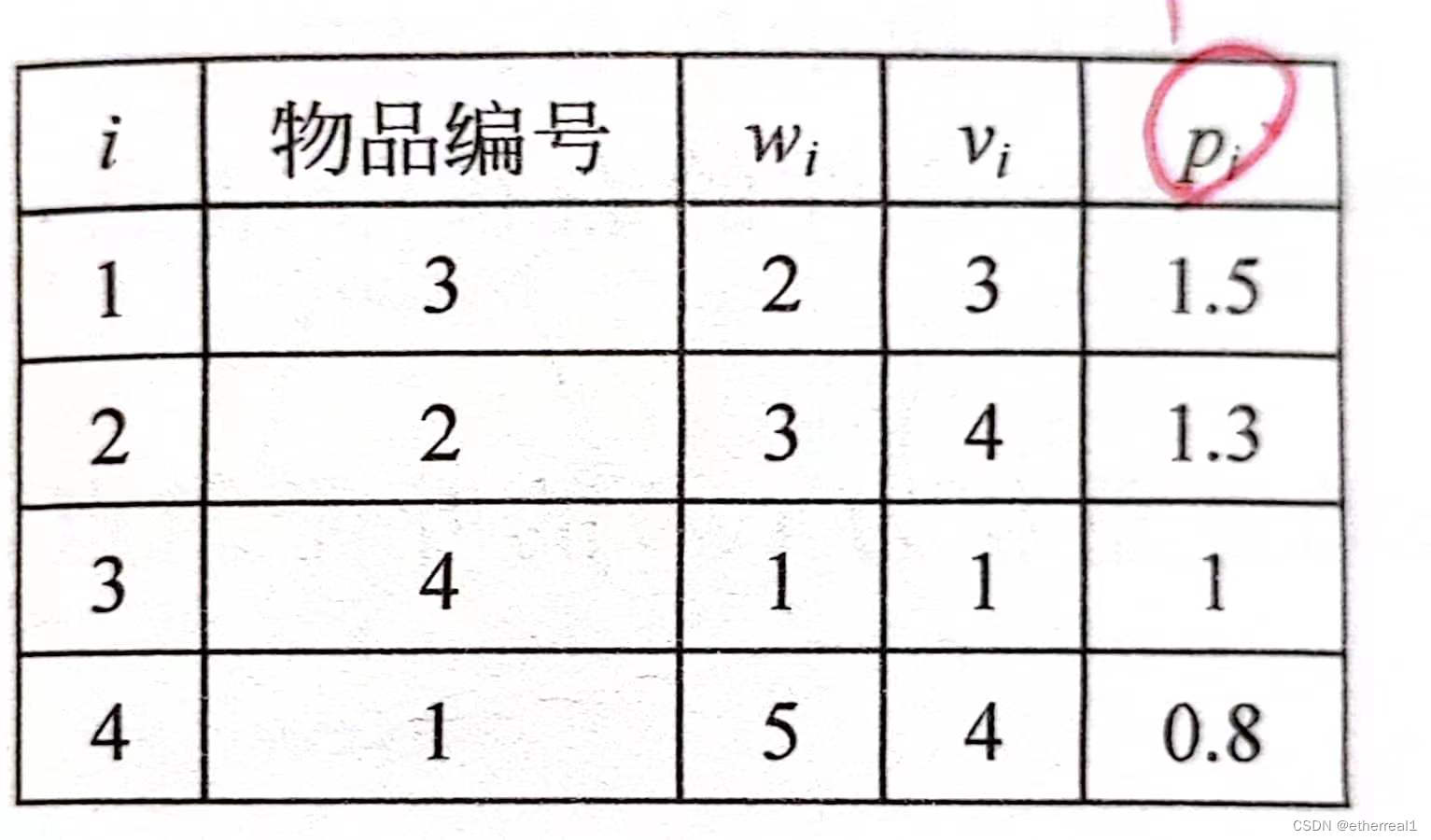
例:对于上图所示物品集合,算法所示的解空间如下:
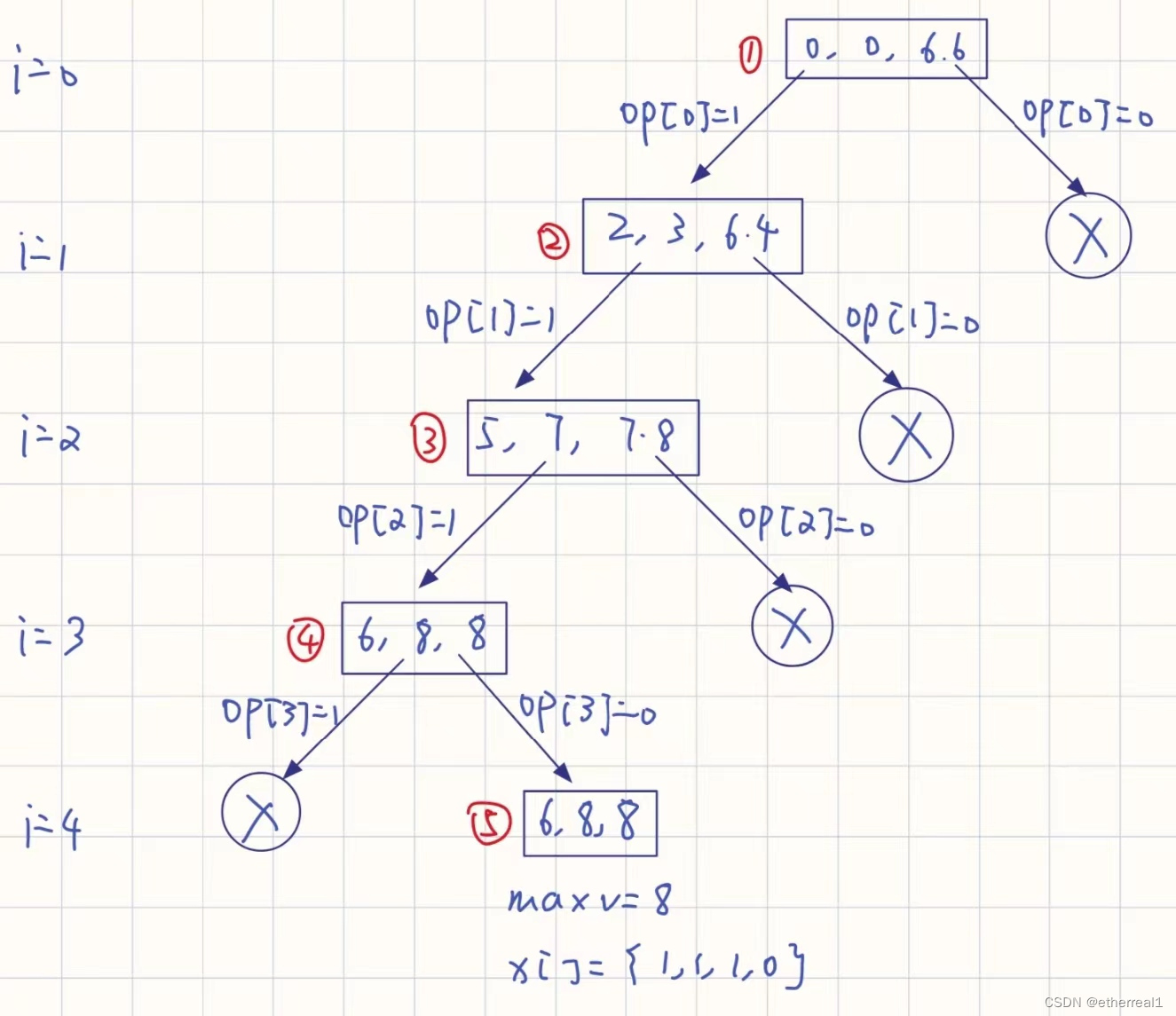
二、代码展示
先定义全局变量
#include <iostream>
#include <malloc.h>
using namespace std;
int w[] = { 5, 3, 2, 1 }; //每个物品的重量
int v[] = { 4, 4, 3, 1 }; //每个物品的价值
int W = 6; //限制背包重量
int n = 4; //物品数目
int maxv = 0; //最大价值
int x[] = { 0, 0, 0, 0 }; //解向量
int num[] = { 1, 2, 3, 4 }; //物品编号,需按照单位重量价值递减重新排列
再设计快速排序算法对p,num,w,v数组进行重排序
int partition(double p[], int num[], int w[],int v[], int str, int end) {
int i = str, j = end;
double p_temp = p[str];
int num_temp = num[str];
int w_temp = w[str];
int v_temp = v[str];
while (i != j) {
while ((i < j) && (p[j] <= p_temp)) {
j--;
}
p[i] = p[j];
num[i] = num[j];
w[i] = w[j];
v[i] = v[j];
while ((i < j) && (p[i] >= p_temp)) {
i++;
}
p[j] = p[i];
num[j] = num[i];
w[j] = w[i];
v[j] = v[i];
}
p[i] = p_temp;
num[i] = num_temp;
w[i] = w_temp;
v[i] = v_temp;
return i;
}
//设计函数对物品按单位价值递减的顺序重新排列
void resort(double p[], int num[], int w[], int v[], int str, int end) {
//用快速排序的方法进行排序
if (str < end) {
int i = partition(p, num, w, v, str, end);
resort(p, num, w, v, str, i - 1);
resort(p, num, w, v, i + 1, end);
}
}
class item { //定义物品类,存放物品信息
public:
double p;
int num;
int w;
int v;
item() {}
item(double p, int num, int w, int v) {
this->p = p;
this->num = num;
this->w = w;
this->v = v;
}
};
设计上述限界函数
int bound(int i, int tw, int tv, item items[]) {
if (i == n) {
return tv;
}
else if (i < n) {
i++;
while ((i < n) && (tw + items[i].w <= W)) {
tw += items[i].w;
tv += items[i].v;
i++;
}
if ((i < n) && (tw + items[i].w < W)) {
tv += (W - tw) * items[i].p;
}
return tv;
}
}
设计回溯算法
void dfs(int i, int tw, int tv, int op[], item items[]) {
if (i == n) {
if ((tw <= W) && (tv > maxv)) {
maxv = tv;
for (int i = 0; i < n; i++) {
x[i] = op[i];
}
}
}
else {
if (tw + items[i].w <= W) {
op[i] = 1;
dfs(i + 1, tw + items[i].w, tv + items[i].v, op, items);
}
if (bound(i, tw, tv, items) > maxv) {
op[i] = 0;
dfs(i + 1, tw, tv, op, items);
}
}
}
主程序调用并输出最终结果
int main() {
double* p = (double*)malloc(sizeof(double) * n);
for (int i = 0; i < n; i++) {
p[i] = (double)v[i] / w[i];
}
resort(p, num, w, v, 0, n - 1);
item items[4];
for (int i = 0; i < n; i++) {
items[i] = item(p[i], num[i], w[i], v[i]);
}
int op[] = { 0, 0, 0, 0 };
dfs(0, 0, 0, op, items);
cout << "最大价值为:" << maxv << endl;
cout << "对应方案为:{";
for (int i = 0; i < n; i++) {
if (x[i] == 1) {
cout << items[i].num;
}
}
cout << "}" << endl;
free(p);
return 0;
}
最终结果显示如下:

三、算法分析
解空间中最多生成2n+1-1个节点,考虑右剪枝中限界函数的计算时间以及复制最优解的时间均为O(n),因此,算法的最坏时间复杂度为O(n x 2n)
分枝限界法
设一个背包问题是:n = 3, 重量为 w = (16, 15, 15), 价值为 v = (45, 25, 25), 背包限重为W = 30,求放入背包总重量小于等于W并且价值最大的解,设解向量为x = (x1, x2, x3)。
队列式分支限界法
一、算法设计
左剪枝函数:当前背包重量 + 当前考虑物品重量 ≤ W,否则剪枝
右剪枝函数:设计上界函数,扩展当前节点时,求出右子节点的上界,若该上界值比当前求出的maxv值小或者相等,则不将该右子节点进队。上界函数设计如下:
// 求指定节点的上界函数值
void bound(Node& node) {
int weight = node.tw;
int ub_value = node.tv;
int k = node.i;
while ((weight + w[k] <= W) && (k < n)) {
ub_value += v[k];
weight += w[k];
k++;
}
if ((weight < W) && (k < n)) {
node.ub = ub_value + (W - weight) * v[k] / w[k];
}
else {
node.ub = ub_value;
}
}
对列中节点类的设计如下:
//定义队列节点类
class Node {
public:
int tw;
int tv;
int i;
int ub;
int op[3];
Node() {}
Node(int tw, int tv, int i) {
this->tw = tw;
this->tv = tv;
this->i = i;
}
};
分支限界法的核心思想是宽度优先搜索,因此,利用队列先进先出的特点来组织节点。扩展节点表示对相应物品选择与否的考虑,例如:对于第0层的节点,扩展该层节点意味着对第0个物品进行考虑。对于非叶节点,左子节点需满足左剪枝函数,右子节点需满足右剪枝函数,满足条件方可进队。
例:对于本题,采用队列式分支限界法得到的解空间树如下:
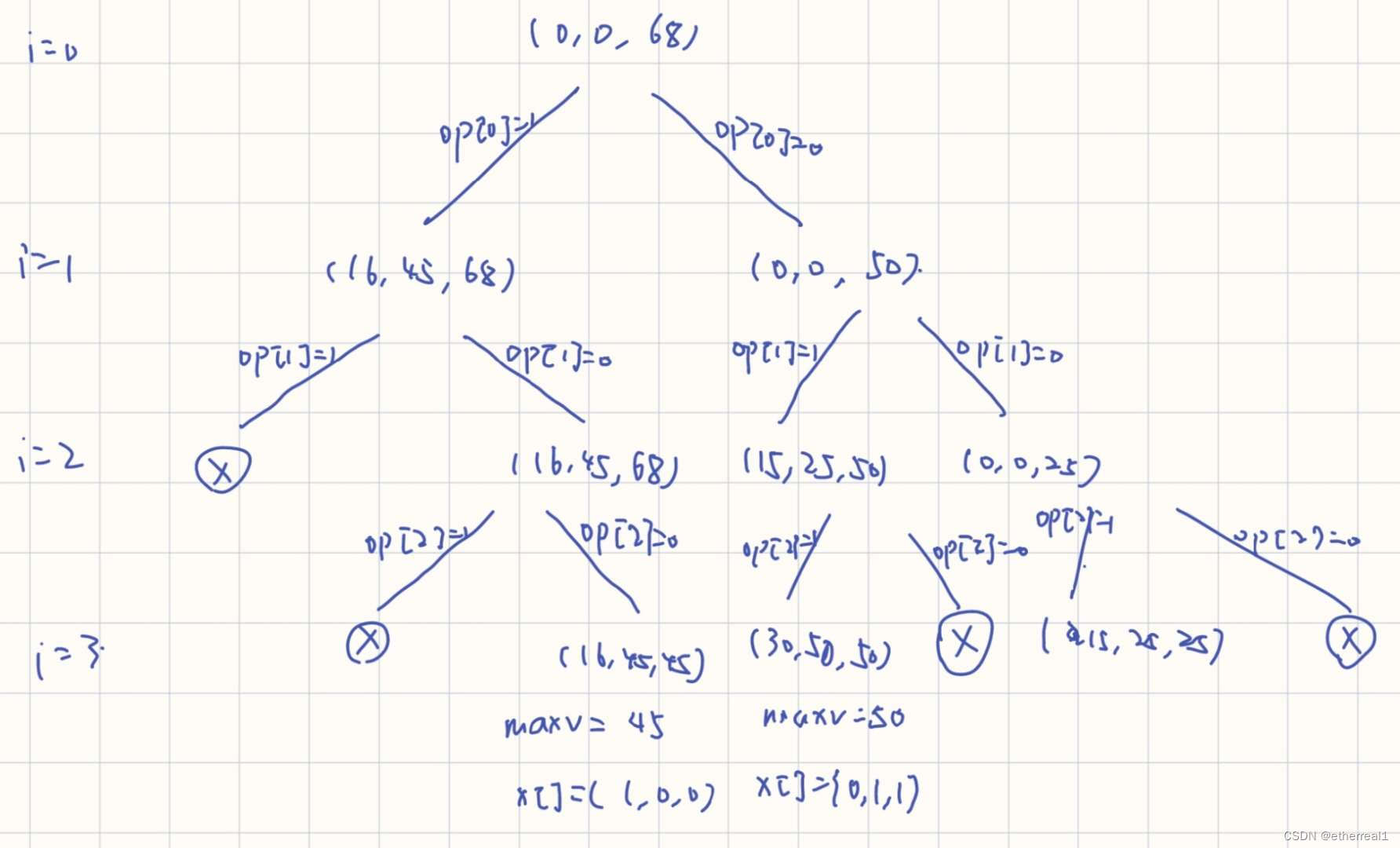
二、代码展示
#include <iostream>
#include <queue>
using namespace std;
int w[] = { 16, 15, 15 }; //每个物品的重量
int v[] = { 45, 25, 25 }; //每个物品的价值
int W = 30; //限制背包重量
int n = 3; //物品数目
int maxv = 0; //最大价值
int x[] = { 0, 0, 0 }; //解向量
//设计队列中的节点类
class Node {
public:
Node(int tw, int tv, int i) {
this->tw = tw;
this->tv = tv;
this->i = i;
}
Node(){}
int tw; // 当前背包重量
int tv; // 当前背包价值
int i; // 节点所处层数
int ub; // 当前节点的上界
int op[3]; // 当前节点对应的解向量
};
void bound(Node& node) { // 求出给定节点的上界
int k = node.i;
int ub_value = node.tv;
int weight = node.tw;
while ((weight + w[k] <= W) && (k < n)) {
ub_value += v[k];
weight += w[k];
k++;
}
if ((weight < W) && (k < n)) {
node.ub = ub_value + (W - weight) * v[k] / w[k];
}
else {
node.ub = ub_value;
}
}
void bfs() {
queue<Node> q;
Node temp(0, 0, 0);
for (int i = 0; i < n; i++) {
temp.op[i] = 0;
}
bound(temp);
q.push(temp);
Node pa, lc, rc;
while (!q.empty()) { // 队不空循环
pa = q.front();
q.pop();
lc.i = pa.i + 1;
lc.tw = pa.tw + w[pa.i];
lc.tv = pa.tv + v[pa.i];
for (int k = 0; k < n; k++) {
lc.op[k] = pa.op[k];
}
lc.op[pa.i] = 1;
bound(lc);
if ((lc.i == n) && (lc.tw <= W)) { // 扩展的左子节点为叶节点
if (lc.tv > maxv) {
maxv = lc.tv;
for (int k = 0; k < n; k++) {
x[k] = lc.op[k];
}
}
}
else if (lc.tw <= W) {
q.push(lc);
}
rc.i = pa.i + 1;
rc.tw = pa.tw;
rc.tv = pa.tv;
for (int k = 0; k < n; k++) {
rc.op[k] = pa.op[k];
}
rc.op[pa.i] = 0;
bound(rc);
if (rc.i == n) { // 扩展的右子节点为叶节点
if (rc.tv > maxv) {
maxv = rc.tv;
for (int k = 0; k < n; k++) {
x[k] = rc.op[k];
}
}
}
else if (rc.ub > maxv) {
q.push(rc);
}
}
}
int main() {
bfs();
cout << "最终结果为:" << endl;
cout << "最大价值为:" << maxv << endl;
cout << "最佳组合为:";
for (int i = 0; i < n; i++) {
cout << x[i] << " ";
}
cout << endl;
return 0;
}
运行结果如下:

优先队列式分支限界法
一、算法设计
采用优先队列式分支限界法,就是将一般的队列改为优先队列,但必须设计限界函数,因为优先级是以限界函数值为基础的。限界函数的设计方法跟上面相同。这里采用最大堆表示活结点表,优先级为活结点所获得的价值。
采用STL容器中的priority_queue容器作为优先队列,其节点与队列式分支限界法中的节点相同,仅需添加对<符号的重载函数,按节点ub值越大越优先出队,设计的重载函数如下:
bool operator<(const Node& node)const {
return ub < node.ub;
}
二、代码展示
#include <iostream>
#include <queue>
using namespace std;
int w[] = { 16, 15, 15 }; //每个物品的重量
int v[] = { 45, 25, 25 }; //每个物品的价值
int W = 30; //限制背包重量
int n = 3; //物品数目
int maxv = 0; //最大价值
int x[] = { 0, 0, 0 }; //解向量
//定义队列节点类
class Node {
public:
int tw;
int tv;
int i;
int ub;
int op[3];
Node() {}
Node(int tw, int tv, int i) {
this->tw = tw;
this->tv = tv;
this->i = i;
}
bool operator<(const Node& node)const {
return ub < node.ub;
}
};
// 求指定节点的上界函数值
void bound(Node& node) {
int weight = node.tw;
int ub_value = node.tv;
int k = node.i;
while ((weight + w[k] <= W) && (k < n)) {
ub_value += v[k];
weight += w[k];
k++;
}
if ((weight < W) && (k < n)) {
node.ub = ub_value + (W - weight) * v[k] / w[k];
}
else {
node.ub = ub_value;
}
}
void bfs() {
priority_queue<Node> q;
Node start(0, 0, 0);
for (int k = 0; k < n; k++) {
start.op[k] = 0;
}
bound(start);
q.push(start);
Node pa, lc, rc;
while (!q.empty()) {
pa = q.top();
q.pop();
lc.i = pa.i + 1;
lc.tw = pa.tw + w[pa.i];
lc.tv = pa.tv + v[pa.i];
for (int i = 0; i < n; i++) {
lc.op[i] = pa.op[i];
}
lc.op[pa.i] = 1;
bound(lc);
if ((lc.i == n) && (lc.tw <= W)) { // 找到了一个合适的左叶节点
if (lc.tv > maxv) {
maxv = lc.tv;
for (int i = 0; i < n; i++) {
x[i] = lc.op[i];
}
}
}
else if (lc.tw <= W) {
q.push(lc);
}
rc.i = pa.i + 1;
rc.tw = pa.tw;
rc.tv = pa.tv;
for (int i = 0; i < n; i++) {
rc.op[i] = pa.op[i];
}
rc.op[pa.i] = 0;
bound(rc);
if ((rc.i == n) && (rc.tv > maxv)) { //找到了一个合适的右叶节点
maxv = rc.tv;
for (int i = 0; i < n; i++) {
x[i] = rc.op[i];
}
}
else if (rc.ub > maxv) {
q.push(rc);
}
}
}
int main() {
bfs();
cout << "最终结果如下:" << endl;
cout << "\t最大价值为:" << maxv << endl;
cout << "\t最佳组合为:";
for (int i = 0; i < n; i++) {
cout << x[i] << " ";
}
cout << endl;
return 0;
}
最终结果如下:

三、算法分析
因为该算法最坏情况下会访问子集树中的所有节点,因此时间复杂度为O(2n)
动态规划法
设一个背包问题是:n = 5, 重量为 w = (2, 2, 6, 5, 4), 价值为 v = (6, 3, 5, 4, 6), 背包限重为W = 10,求放入背包总重量小于等于W并且价值最大的解,设解向量为x = (x1, x2, x3, x4, x5)。
一、算法设计
在该问题中需要确定x1, x2, …, xn的值。假设按i = 1, 2, …, n的次序来确定xi的值,对应n次决策即n个阶段。
如果置x1 = 0, 则问题变为相对于其余物品(即物品2, 3, …, n),背包容量仍为W的背包问题;若置x1 = 1,问题就转变为关于最大背包容量为W - w1的问题。
在决策xi时问题处于以下两种状态:
(1) 背包中不装入物品i,则xi = 0,背包不增加重量和价值,背包余下容量r不变。
(2) 背包中装入物品i,则xi = 1,背包中增加重量wi和价值vi,背包余下容量r = r - wi。
设置二维动态规划数组dp,dp[i][r]表示背包剩余容量为r(0 ≤ r ≤W),已考虑物品1, 2, …, i(1 ≤ i ≤ n)时背包装入物品的最优价值。对应的状态转移方程如下:

例:对于上述问题,采用动态规划法解得的二维动态规划数组如下:
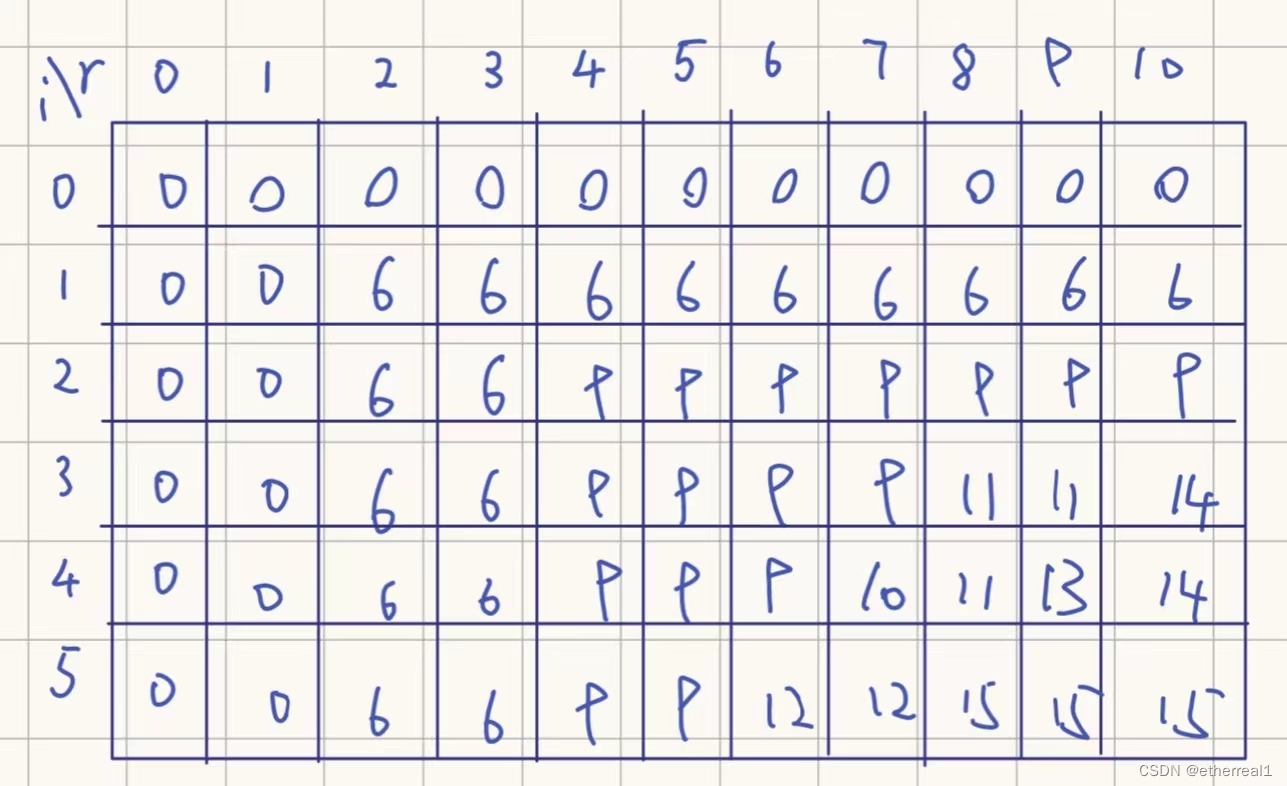
dp[n][W]即为最终结果
在dp数组计算出来后,推导解向量x的过程十分简单,从dp[n][W]开始:
(1) 若dp[i][r] ≠ dp[i - 1][r],状态转移方程中的第三个条件不成立,并且只满足第4个条件中放入物品i的情况,即dp[i][r] = v[i] + dp[i - 1][r - w[i]],置x[i] = 1,累计总价值maxv += v[i],递减剩余重量r -= w[i]
(2) 若dp[i][r] = dp[i - 1][r],表示物品i放不下或者不放入物品i
例:上述问题回推最优解的过程如下:

最后得到x为{1, 1, 0, 0, 1},背包装入物品总重量为8,总价值为15
二、代码展示
#include <iostream>
#include <malloc.h>
using namespace std;
int w[] = { 0, 2, 2, 6, 5, 4 }; //每个物品的重量
int v[] = { 0, 6, 3, 5, 4, 6 }; //每个物品的价值
int W = 10; //限制背包重量
int n = 5; //物品数目
int maxv = 0; //最大价值
int x[] = { 0, 0, 0, 0, 0, 0 }; //解向量
void dynamic(int**& dp) {
for (int i = 0; i <= W; i++) {
dp[0][i] = 0;
}
for (int i = 0; i <= n; i++) {
dp[i][0] = 0;
}
for (int i = 1; i <= n; i++) {
for (int r = 1; r <= W; r++) {
if (r < w[i]) {
dp[i][r] = dp[i - 1][r];
}
else {
dp[i][r] = max(dp[i - 1][r], v[i] + dp[i - 1][r - w[i]]);
}
}
}
}
void back_track(int** dp) {
maxv = dp[n][W];
int i = n, r = W;
while (i != 0) {
if (dp[i][r] == dp[i - 1][r]) {
x[i] = 0;
i--;
}
else {
x[i] = 1;
r -= w[i];
i--;
}
}
}
int main() {
int** dp;
dp = (int**)malloc(sizeof(int*) * (n + 1));
for (int i = 0; i <= n; i++) {
dp[i] = (int*)malloc(sizeof(int) * (W + 1));
}
dynamic(dp);
back_track(dp);
cout << "最终结果如下:" << endl;
cout << "\t最大价值为:" << maxv << endl;
cout << "\t解向量为:";
for (int i = 1; i <= n; i++) {
cout << x[i] << " ";
}
cout << endl;
for (int i = 0; i <= n; i++) {
free(dp[i]);
}
free(dp);
return 0;
}
运行结果如下:

三、算法分析
该算法的时间复杂度分析很简单,为O(nW)。
求解背包问题
设有编号为1、2、…、n的n个物品,它们的重量分别为w1, w2, …, wn,价值分别为v1, v2, …, vn,有一个背包可以携带的最大重量不超过W,求解目标是在不超过背包负重的前提下使背包装入的总价值最大。与0/1背包问题的区别是,这里的每个物品可以取一部分装入背包。
贪心法
一、算法设计
贪心原则:优先选择单位重量下价值最大的物品。
因此,需对所有物品按单位重量价值递减排列,本例采用快速排序算法
二、代码展示
#include <iostream>
#include <malloc.h>
using namespace std;
int w[] = {10, 20, 30, 40, 50}; //每个物品的重量
int v[] = {20, 30, 66, 40, 60}; //每个物品的价值
int W = 100; //限制背包重量
int n = 5; //物品数目
int maxv = 0; //最大价值
double x[] = { 0, 0, 0, 0, 0}; //解向量
class Item {
public:
int num; //物品编号
int w; //物品重量
int v; //物品价值
double p; //物品单位重量价值
};
int partition(Item* item_list, int str, int end) {
int i = str, j = end;
Item temp = item_list[str];
while (i != j) {
while ((i < j) && (item_list[j].p < temp.p)) {
j--;
}
item_list[i] = item_list[j];
while ((i < j) && (item_list[i].p > temp.p)) {
i++;
}
item_list[j] = item_list[i];
}
item_list[i] = temp;
return i;
}
void quick_sort(Item* item_list, int str, int end) {
if (str >= end) {
return;
}
else {
int i = partition(item_list, str, end);
quick_sort(item_list, str, i - 1);
quick_sort(item_list, i + 1, end);
}
}
void find_solution(Item* item_list) {
int weight = 0;
int i = 0;
while ((weight + item_list[i].w <= W) && (i < n)) {
weight += item_list[i].w;
maxv += item_list[i].v;
x[item_list[i].num] = 1;
i++;
}
if ((weight < W) && (i < n)) {
maxv += item_list[i].p * (W - weight);
x[item_list[i].num] = (double)(W - weight) / item_list[i].w;
}
}
int main() {
Item* item_list = (Item*)malloc(sizeof(Item) * n);
for (int i = 0; i < n; i++) {
item_list[i].num = i;
item_list[i].w = w[i];
item_list[i].v = v[i];
item_list[i].p = (double)v[i] / w[i];
}
quick_sort(item_list, 0, n - 1);
find_solution(item_list);
cout << "求解结果如下:" << endl;
cout << "\t最大价值为:" << maxv << endl;
cout << "\t解向量如下:";
for (int i = 0; i < n; i++) {
cout << x[i] << " ";
}
cout << endl;
free(item_list);
return 0;
}
运行结果如下:

三、算法分析
快速排序算法的时间复杂度为:O(n x logn),一重循环的时间复杂度为:O(n),因此,总的时间复杂度为:O(n x logn)






















 1079
1079











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








