理解 PyTorch 中维度的概念

我这一篇文章里的所有的动图，都是来自与下面这篇文章，写的非常直观。

原文链接(十分棒的文章), Understanding dimensions in PyTorch

理解 PyTorch 维度概念

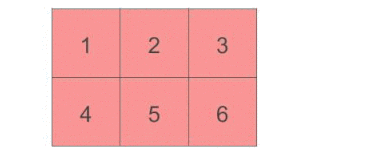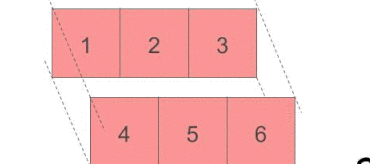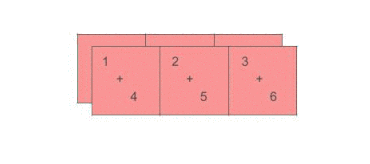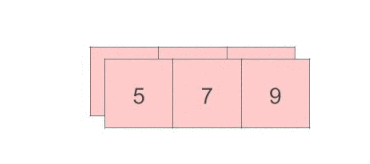
首先我们从最基础的开始, 当我们在 Pytorch 中定义一个二维的 tensor 的时候, 他包含行和列. 例如下面我们创建一个 2✖3 的tensor。

x = torch.tensor([
        [1,2,3],
        [4,5,6]
    ])
# 我们可以看到"行"是dim=0, "列"是dim=1
print(x.shape)
>> torch.Size([2, 3])

我们可以看到打印的结果显示:

• first dimension (dim=0) stays for rows, 第一个维度代表行, 因为是2, 实际x就是2行
• the second one (dim=1) for columns, 第二个维度代表列, 因为是3

于是, 我们会认为, torch.sum(x, dim=0)就是(1+2+3, 4+5+6)=tensor([6, 15]), 但是实际情况却不是这个样子的.

torch.sum(x, dim=0)
>> tensor([5, 7, 9])

我们可以看到按照 dim=0 求和, 其实是在按列相加, 也就是 (1+4, 2+5, 3+6) =tensor([5, 7, 9]), 和我们想象的完全不一样. 我们再看一下按照 dim=1 进行求和.

torch.sum(x, dim=1)
>> tensor([ 6, 15])

可以看到, 在按照 dim=1 的时候求和的时候, 其实在按照按行进行求和,  (1+2+3, 4+5+6)=tensor([6, 15]), 这就让人很困惑, 明明上面说的是 dim=0 代表是行。

于是, 原文作者在一篇介绍 numpy 维度的文章中, 找到了问题的关键所在. 也就是下面的这段话( numpy 中的 axis 也就是这里的 dim).

The way to understand the "axis" of numpy sum is that it collapses the specified axis. So when it collapses the axis 0 (the row), it becomes just one row (it sums column-wise).

上面的话简单翻译就是, 当按照axis=0进行求和的时候, 其实可以想象为对axis=0这个维度进行挤压, 最后只剩下一行, 那一行就是结果, 也就是按列在相加.

是不是还是会有一些困惑, 我们还是对于上面的例子(tensor([[1,2,3], [4,5,6]])), 看一下在dim=0的时候, 为什么是列相加, 以及上面的collapse the specific axis(dim)的含义.

如上面的动图所示, 当dim=0的时候, 按每一行的元素进行相加, 最后的结果就是和按列求和.

对于三维向量

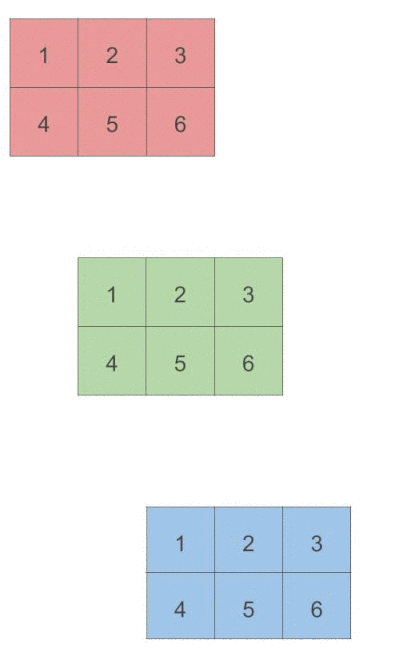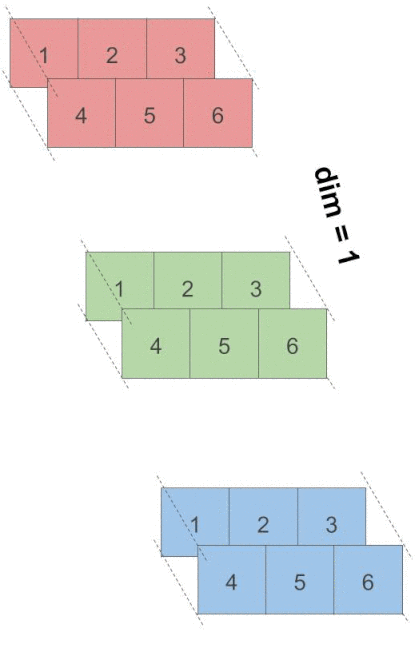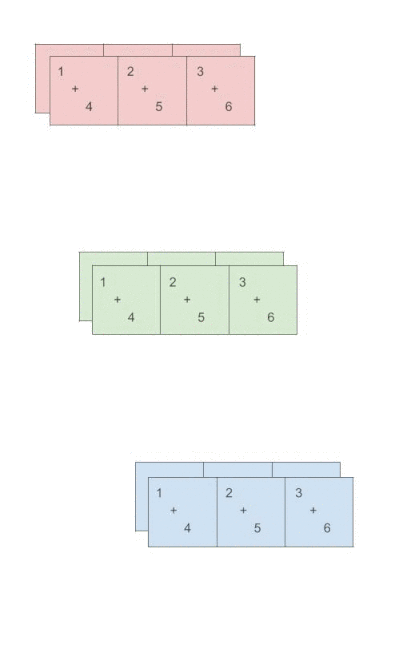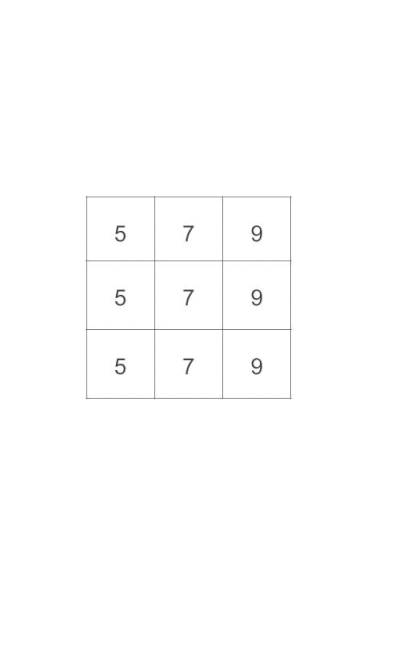
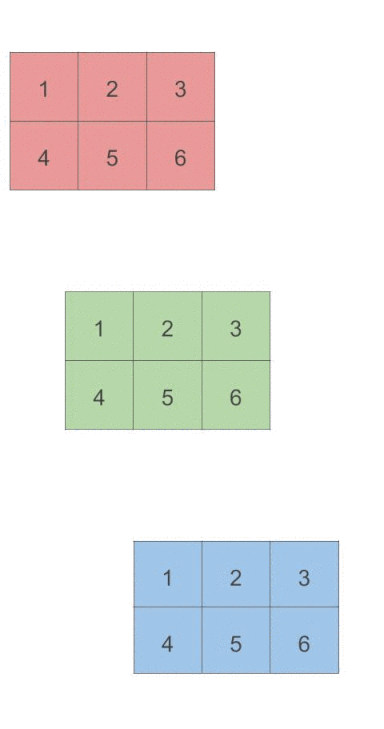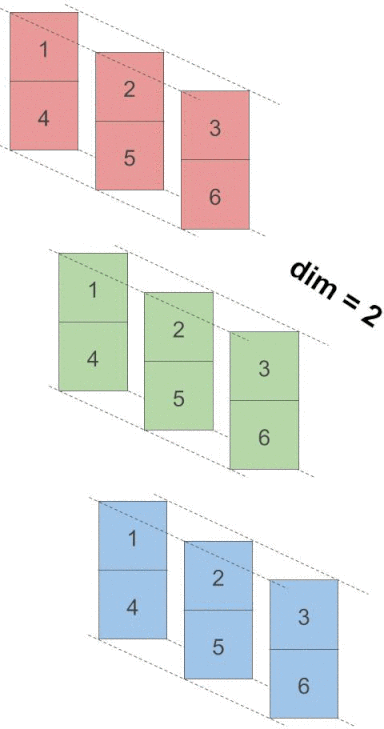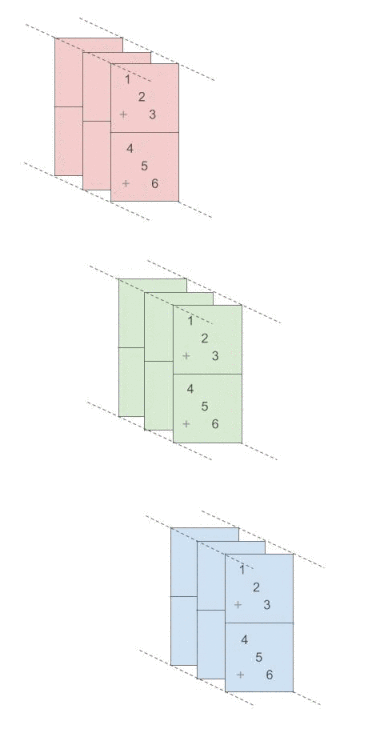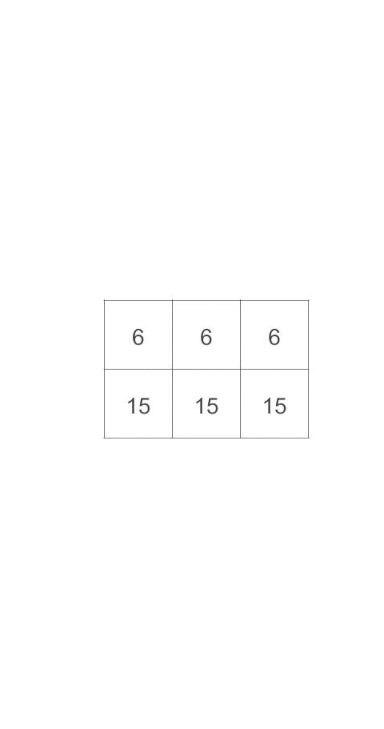
下面我们更进一步, 来看一下对于三维的tensor, 在各个维度进行sum操作的结果. 首先我们看一下每一个dim代表的含义.

# 看一下三维的
x = torch.tensor([
        [
         [1,2,3],
         [4,5,6]
        ],
        [
         [1,2,3],
         [4,5,6]
        ],
        [
         [1,2,3],
         [4,5,6]
        ]
    ])
# 我们可以看到第三维是dim=0, "行"是dim=1, 列是dim=2
print(x.shape)
>> torch.Size([3, 2, 3])

可以看到此时dim=0是第三个维度, dim=1是行, dim=2是列.

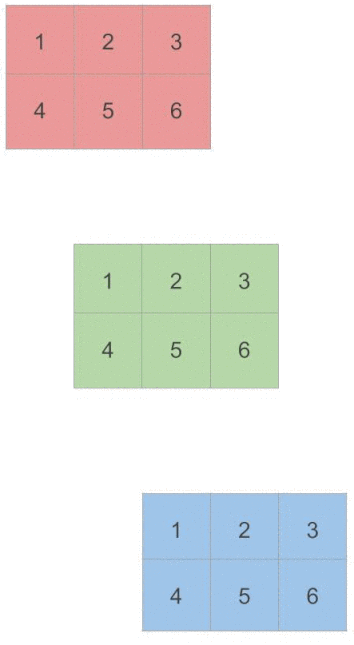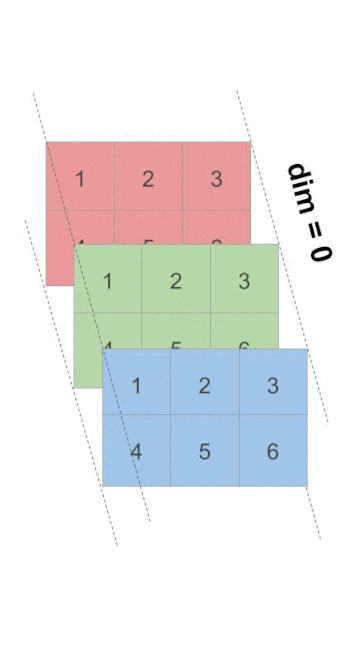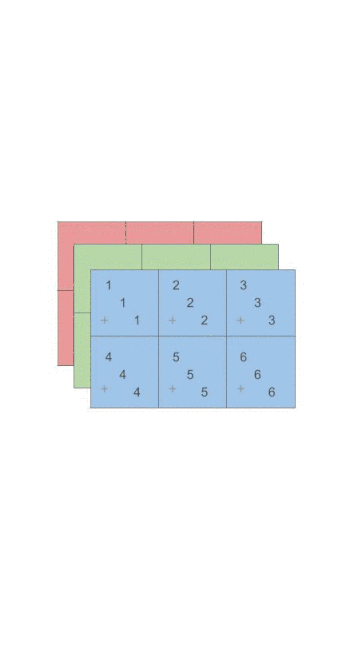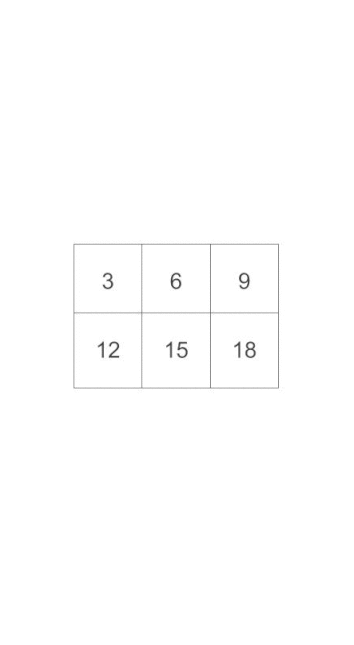
torch.sum(x, dim=0)
>>
tensor([[ 3,  6,  9],
        [12, 15, 18]])

我们可以将其看成是各个二维平面对应元素求和, 还是有点绕, 还是直接看下面的动图.

接着是对dim=1进行求和.

torch.sum(x, dim=1)
>>
tensor([[5, 7, 9],
        [5, 7, 9],
        [5, 7, 9]])

还是直接看下面的动图, 来进行理解.

最后按照dim=2来进行求和.

torch.sum(x, dim=2)
>>
tensor([[ 6, 15],
        [ 6, 15],
        [ 6, 15]])

还是使用动图来进行解释.