目录:
什么是树状数组?
代码模板
原理 + lowbit解释
什么是树状数组?
树状数组作为一种高效的数据结构,可以在O(logn)内完成更新和查询操作,因此非常适合加减, 区间和, 查询。
适合问题:动态连续和查询问题:给定一个n个元素的数组A1,A2,…,An,你的任务是设计一个数据结构,支持以下两种操作。
- add(x,d)操作:让Ax增加d。
- query(L,R):计算AL+AL+1+…+AR。
代码模板
struct BIT {
int n; // 树的大小
vector<LL> C; // 存储树的节点值
BIT(int _n) : n(_n), C(_n + 2) {} // 构造函数,初始化树的大小和节点值
inline int lowbit(int x) { return x & -x; } // 计算二进制中最低位的1对应的整数
void add(int x, LL v) { // 在位置x上增加值v
while (x <= n)
C[x] += v, x += lowbit(x); // 遍历x的所有上级节点,更新节点值
}
LL sum(int x) { // 计算从1到x的所有值的和
LL s = 0;
while (x)
s += C[x], x -= lowbit(x); // 遍历x的所有下级节点,累加节点值
return s;
}
};!!!推荐大家自己动手敲一遍, 尽量背。
原理解释
构造函数
对这个感兴趣的可以去关注博客, 有六季类与结构体的专题。
这里简单讲一下概念, 构造函数就是在构造和访问函数时运行的代码。
这里, 的这个写法意思就是在结构体中查询有一个名叫num的变量初始化是num(),再括号里填入_num, num 是个 int 变量 所以等价于 num = _num, C 是个 vector 所以等价于 C.resize(_num + 2)
student(int _num):num(_num){}再来看一下lowbit
lowbit
详细链接 : https://www.kdocs.cn/l/cvTe0OBF81XO?openfrom=docs
概念:
对于正整数x,我们定义lowbit(x)为x的二进制表达式中最右边的1所对应的值(而不是这个比特的序号)。比如,38 288的二进制是1001010110010000,所以lowbit(38 288)=16(二进制是10 000)。在程序实现中,lowbit(x)=x&-x。为什么呢?回忆一下,计算机里的整数采用补码表示,因此-x实际上是x按位取反,末尾加1以后的结果,如下图所示。
![]()
二者按位取“与”之后,前面的部分全部变0,之后lowbit保持不变。如下图所示是一棵典型的BIT,由15个结点组成,编号为1~15。
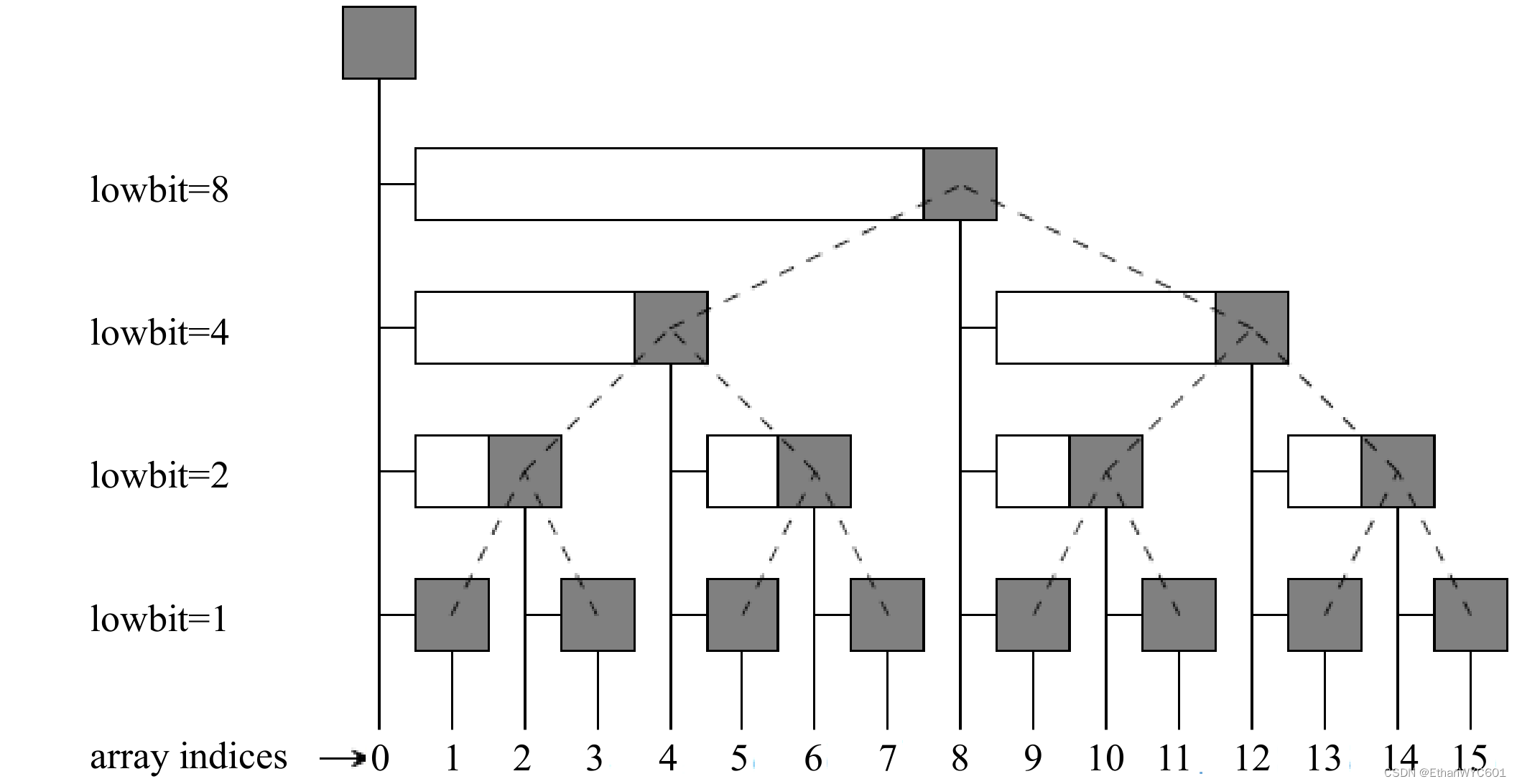
其余的可以访问链接, 但最好还是自己动手演算一下。
























 1065
1065

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








