【C++】树状数组

定义

所谓树状数组，逻辑结构是一棵树，但是采用数组实现，他能解决单点修改区间查询类的问题，属于前缀和的一种优化。

lowbit

学习树状数组，首先要引入$lowbit$概念，所谓$lowbit$，指的是二进制数最低位的$1$的权值，比如二进制数$1100$的lowbit就是二进制表示就是$100$，也就是权值为$2^2=4$，下文中我们用$lowbit(x)$表示$x$的$lowbit$值。实际上，$lowbit(x)=x\&(-x)$，$\&$表示按位与运算。

inline int lowbit(int i){return i&(-i);}

树状数组结构

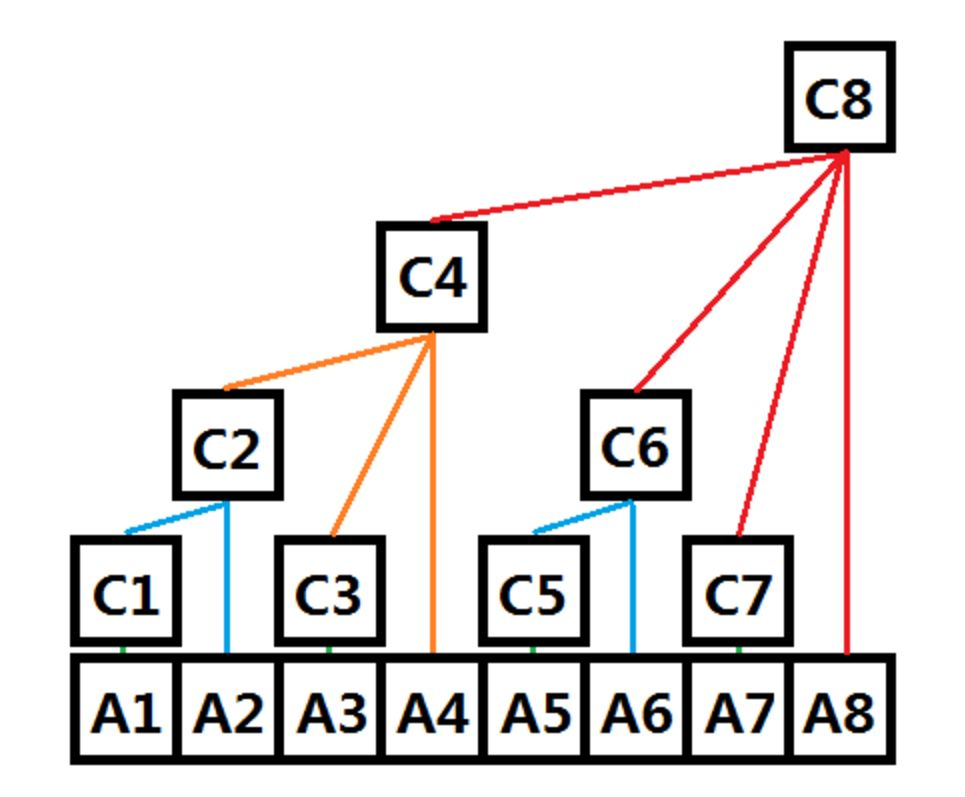
上图摘自orangebird，在图中$A_i$表示原数组，$C_i$表示$A_i$对应的树状数组。

$C_i$维护的是$A_i$区间信息，那么$C_i$究竟维护什么区间呢？我们可以先计算下$lowbit(i)$：

lowbit(1)=1
lowbit(2)=2
lowbit(3)=1
lowbit(4)=1
lowbit(5)=1
lowbit(6)=2
lowbit(7)=1
lowbit(8)=8

我们可以发现，$C_i$维护的长度就是$lowbit(i)$，维护区间是$[i-lowbit(i)+1,i]$。

如$C3$维护的区间是$[2-lowbit(2)+1,2]$即$[1,2]$，$C8$维护的区间是$[8-lowbit(8)+1,8]$即$[1,8]$。

那么树状数组的$C_i$可能会影响哪些位的值呢？以$C1$为例，$1+lowbit(1)=2，2+lowbit(2)=4，4+lowbit(4)=8$，我们发现第$i$个数值会递归影响所有的父结点，在树状数组中编号为$i$的结点的父结点编号为$i+lowbit(i)$。

应用举例

单点修改区间和查询

考虑一类问题，给出长度为$len$的连续区间，并给出每个端点的初始值，现允许在询问的过程中进行单点修改，每次询问的是区间$[l,r]$的和。

我们可以转化连续区间为$[1,len]$的树状数组，假设$A$为原数组，$C_i$为所维护的树状数组，维护的是区间和信息。

更新函数

• 由于树状数组初始化需要借用更新函数，故放到前面。所做的工作是将编号$i$与$i$所影响的编号位置都增加$x$，减小可以认为是增加$-x$。

void update(int i,int x){
	while(i<=len){
		C[i]+=x;//加上x
		i+=lowbit(i);//下一个被影响的i
	}
}

初始化函数

void init(){
	memset(C,0,sizeof(C));//初始化C数组为0
	for(int i=1;i<=len;i++){
		update(i,A[i]);//递归插入A[i]
	}
}

前缀和查询

• 由于树状数组维护的是区间$[i-lowbit(i)+1,i]$，我们无法直接求得$[l,r]$的和，所以我们先求$[1,i]$的和，记为$Sum(i)$，则$Su{m}_{[l,r]}=Sum(r)-Sum(l-1)$。

int Sum(int i){//计算[1,i]的和
	int sum=0;
	while(i){
		sum+=C[i};//在区间内
		i-=lowbit(i);//上一个未被影响的编号
	}
	return sum;
}

区间查询

• 根据差分思想，即可求得$[l,r]$的和，即$Su{m}_{[l,r]}=Sum(r)-Sum(l-1)$。

int query(int l,int r){
	return Sum(r)-Sum(l-1);
}

区间修改单点查询

考虑一类问题，给出长度为$len$的连续区间，并给出每个端点的初始值，现允许在询问的过程中增减某个区间，每次询问的是点$i$的值。

我们可以转化连续区间为$[1,len]$的树状数组，假设$A$为原数组，$C_i$为所维护的树状数组。

此问题需要引入差分数组$B_i$，$B_i$记录的是$A_i-A_{i-1}$，不难发现${\sum }_{i=1}^n{B}_i=A_n$。$C_i$则维护$B_i$的区间$[l,r]$和，因此${\sum }_{i=1}^n{C}_i=A_n$。

当区间$[l,r]$增加$x$时，$C_l$增加$x$即可表示$A_l\sim A_r$均增加$x$，但是相应的$A_{r+1}\sim A_{len}$也被影响了，所以$C_{r+1}$需要减少$x$才能保证后续区间不被影响。

更新函数

void update(int i,int x){
	while(i<=len){
		C[i]+=x;//加上x
		i+=lowbit(i);//下一个被影响的i
	}
}

初始化函数

void init(){
	memset(C,0,sizeof(C));//初始化C数组为0
	for(int i=1;i<=len;i++){
		update(i,A[i]-A[i-1]);//递归插入B[i]=A[i]-A[i-1],注意需要A[0]=0
	}
}

区间修改

void change(int l,int r,int x){
	update(l,x);
	update(r+1,-x);
}

单点查询

int query(int i){
	int sum=0;
	while(i){
		sum+=C[i];
		i-=lowbit(i);
	}
	return sum;
}

区间最值问题

考虑一类问题，给出长度为$len$的连续区间，并给出每个端点的初始值，现允许在询问的过程中进行单点修改，每次询问的是区间$[l,r]$的最大或最小值信息。

我们可以转化连续区间为$[1,len]$的树状数组，假设$A$为原数组，$C_i$为所维护的树状数组，记录的是$[i-lowbit(i)+1,i]$的最值。

更新函数

void update(int i,int x){
	while(i<=len){
		if(visit[i]){//如果i已被访问,需引入visit数组记录i是否被访问
			C[i]=max(C[i],x);
			//或C[i]=min(C[i],x);
		}else{
			C[i]=x;
		}
		i+=lowbit(i);//下一个被影响的i
	}
}

初始化函数

void init(){
	memset(visit,0,sizeof(visit));//初始化visit数组为0
	for(int i=1;i<=len;i++){
		update(i,A[i]);//递归插入B[i]=A[i]-A[i-1],注意需要A[0]=0
	}
}

查询函数

1. 每次记录$C[r]$，然后令$r=r-1$，跳到第二步
2. 查询$[r-lowbit(r)+1,r]$所维护的区间，更新$r=r-lowbit(r)$直到$l$在$r$的区间内，跳到第三步
3. 重复第一步直到$l=r$

int query(int l,int r){
	int M=A[r];
	while(1){
		M=max(M,A[r]);
		//或M=min(M,A[r]);
		if(r==l) break;
		for(r=r-1;l<=r-lowbit(r);r-=lowbit(r)){//保证l不在r维护区间内才循环
			M=max(M,C[r]);
			//或M=min(M,C[r]);
		}
	}
	return M;
}