新手数学建模教程，保姆级教程。_通过判断矩阵计算各要素相对于上一层次要素的权重。设判断矩阵为a=(aij)n×n,其特-CSDN博客

本文链接：https://blog.csdn.net/2301_79729084/article/details/147260688

分工

1.论文:mathtype (Latex)

2.建模；相应的建模知识与撰写方法，写摘要

3.编程:matlab、SPSs、(Python)

意见

1.一般用非线性模型或者多目标，这样复杂一些。

2.要查文献。

3.结果写的详细一点，让人容易理解。

4.spearman相关系数可以画一个热力图。

5.matlab只有掌握一些基础的语法。

数学建模需要资料搜索，数学建模，编程解决和撰写论文。

评价模型

1. 层次分析法

①层次分析法是一种多目标、多准则的决策问题

②层次分析法是一种主观加权法

层次分析法解决评价类问题的方法。

③层次分析法通过以下步骤实现:
1.画层次结构图:将问题分解为目标层、准则层和方案层。（出现在论文中）
2.构造判断矩阵:通过两两比较，确定各因素的相对重要性。（确定评价指标的孰轻孰重）
3.权重计算:计算各因素的权重向量。
4.一致性检验:检验判断矩阵的一致性，确保逻辑合理。
综合权重计算:逐层合成权重，得到最终评价结果。

1.2 层次分析法建模
Step1:构建层次结构将问题分解为目标层、准则层和方案层。

目标层:明确决策的最终目标。

准则层:列出影响决策的主要因素或准则。

方案层:提供可供选择的方案或备选对象。

Step2:构造判断矩阵
对同一层次的各因素，通过两两比较的方式，确定其相对重要性。采用1-9的标度法:
1:两个因素同等重要
3:一个因素比另一个稍微重要
5:一个因素比另一个明显重要
7:一个因素比另一个强烈重要
9:一个因素比另一个极端重要
构造判断矩阵A-(a)，其中a表示第i个因素相对于第j个因素的重要性

Slep3:一致性检验
由于判断矩阵基于主观比较，可能存在不一致性，因此需要进行一致性检验:

Step4:计算权重向量

通过判断矩阵计算各因素的权重:

% 层次分析法 (AHP) 示例代码

% 输入判断矩阵
disp('请输入判断矩阵（n x n 的正互反矩阵）：');
disp('例如：');
disp('[1 3 5; 1/3 1 2; 1/5 1/2 1]');
A = input('输入判断矩阵 A = ');

% 获取矩阵大小
[n, ~] = size(A);

% 计算权重向量
% 方法1：几何平均法
geo_mean = prod(A, 2).^(1/n); % 每行元素的几何平均值
weights_geo = geo_mean / sum(geo_mean); % 归一化

% 方法2：特征向量法
[V, D] = eig(A); % 求特征向量和特征值
[max_eig_val, max_idx] = max(diag(D)); % 找到最大特征值及其索引
weights_eig = V(:, max_idx) / sum(V(:, max_idx)); % 归一化后的特征向量

% 输出权重
disp('几何平均法计算的权重：');
disp(weights_geo');
disp('特征向量法计算的权重：');
disp(weights_eig');

% 一致性检验
CI = (max_eig_val - n) / (n - 1); % 一致性指标
RI = [0 0 0.58 0.90 1.12 1.24 1.32 1.41 1.45 1.49]; % 随机一致性指标
if n > 1 && n <= length(RI)
    CR = CI / RI(n); % 一致性比率
    disp(['一致性比率 CR = ', num2str(CR)]);
    if CR < 0.1
        disp('判断矩阵通过一致性检验，结果可靠。');
    else
        disp('判断矩阵未通过一致性检验，请重新检查判断矩阵。');
    end
else
    disp('无法进行一致性检验，请检查矩阵维度或随机一致性指标表。');
end

使用说明

输入判断矩阵：
- 判断矩阵是一个 n×n的正互反矩阵，表示各因素之间的相对重要性。
- 矩阵的对角线元素为 1，且满足 aij=1/aji。
运行代码：
- 将上述代码复制到 MATLAB 脚本文件中并运行。
- 根据提示输入判断矩阵。
输出结果：
- 几何平均法和特征向量法计算出的权重。
- 一致性比率（CR），如果 CR<0.1CR<0.1，则判断矩阵具有可接受的一致性。

层次分析法（Analytic Hierarchy Process, AHP）是一种多准则决策分析方法，适用于解决复杂决策问题。它通过将决策问题分解为多个层次结构，从最高层的目标到中间层的准则，再到最低层的选项或方案，使得复杂的决策过程变得系统化和易于理解。AHP特别适合以下几类问题：

资源分配：例如，在预算有限的情况下决定如何分配资金给不同的项目或部门。
选择最佳方案：比如在购买产品时比较不同品牌的产品，或者选择最适合某个项目的供应商。
冲突解析：当涉及到多方利益相关者且他们的偏好可能相冲突时，AHP可以帮助找到一个折中的解决方案。
绩效评估：对员工、团队或组织的绩效进行评估，尤其是在有多个评估标准的情况下。
战略规划：帮助企业确定长期目标，并根据这些目标的重要性来制定战略计划。
优先级设定：如在项目管理中确定任务的优先级，确保最关键的任务首先得到处理。
风险评估：评估不同风险因素的相对重要性，以便制定有效的风险管理策略。

AHP的核心在于通过成对比较的方法来量化人的主观判断，进而计算出每个选项相对于整体目标的权重。这种方法能够有效地结合定量数据和定性判断，因此在需要考虑多种因素、尤其是那些难以量化的因素时非常有用。此外，AHP还可以用于验证决策的一致性，从而提高决策过程的可靠性和透明度。

2.熵权法

2.1熵权法原理
①熵权法是一种客观加权法

②可以采用主观加权法修正客观加权法的结果

③信息熵的概念:信息熵是信息论中用于衡量系统不确定性的指标。

熵值越大，表示数据的离散程度越高，不确定性越大:熵值越小，表示数据越集中，不确定性越小。
在熵权法中，指标的熵值反映了该指标对评价结果的贡献程度:
如果某个指标的数据差异较大(离散程度高)，则其值较小，说明该指标包含的信息量
较多，应赋子较大的权重。
如果某个指标的数据差异较小(离散程度低)，则其值较大，说明该指标包含的信息量。

计算公式：通过标准化数据→计算熵值→确定权重，最终加权得到综合评分

数据标准化（或归一化）

是将不同单位、不同量纲的原始数据，转化为统一尺度的过程。简单来说，就是让所有数据站在同一条“起跑线”上。

举个栗子🌰：假设要比较学生的数学成绩（满分150分）和英语成绩（满分100分）。如果直接相加总分，数学成绩天然比英语成绩“占便宜”（比如数学120分，英语80分，数学看似贡献更大）。标准化后，两门课的成绩都转化为0-1之间的数值，就能公平比较每门课的“真实贡献度”。

Min-Max归一化，将数据缩放到[0,1]区间。

数据标准化就像把不同单位的“语言”翻译成统一的“普通话”，让所有指标能公平参与计算。它是熵权法客观性的基石，确保权重分配仅由数据本身的差异决定，而非数值大小或单位的影响。

解决的问题与应用场景

多指标权重分配
- 例子：评估城市发展水平时，涉及经济、环境、教育等多个指标。熵权法能根据各指标数据波动（变异程度）自动分配权重，波动大的指标（如GDP差异明显）权重更高。
- 适用领域：企业绩效评价、投资决策、资源分配、政策效果评估等。
消除主观偏差
- 传统问题：专家打分法可能受个人偏好影响，导致权重不合理。
- 熵权法优势：完全依赖数据计算，结果更客观。例如在硕士论文中分析影响因素时，能减少人为干扰。
处理复杂数据的综合评价
- 例子：评估智能汽车HUD设计时，结合熵权法与VIKOR方法，通过数据标准化和权重计算，选出最优方案。
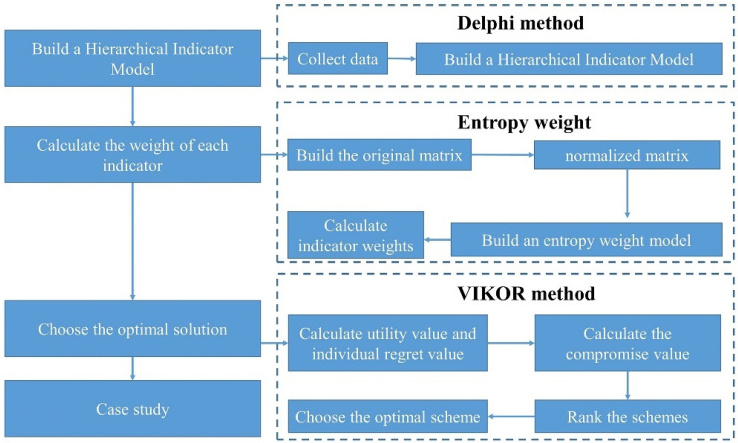
- 技术场景：常与TOPSIS、AHP等方法结合，优化决策流程。
区分正负向指标
- 例子：在生态系统健康评估中，正向指标（如植被覆盖率越高越好）和负向指标（如污染指数越低越好）需分别标准化处理，熵权法能自动适配。

熵权法像一台“自动天平”，通过分析数据波动的大小，判断每个指标的“区分能力”，从而客观分配权重。它特别适合处理需要科学量化、减少主观影响的复杂决策问题，如学术研究中的多因素分析、企业绩效排名等。但需注意，实际应用中常与其他方法结合（如AHP-熵权法），以提升结果的全面性和稳定性。

1. 生成随机数据

n = 5; % 样本数量
m = 4; % 指标数量
data = rand(n, m); % 生成随机数据矩阵 (n×m)
disp('原始数据矩阵:');
disp(data);

这部分代码用于生成一个随机数据矩阵 data，其中 n 是样本数量，m 是指标数量。
rand(n, m) 生成一个 n×m 的随机矩阵，矩阵中的元素在 [0, 1) 范围内。
disp 函数用于显示矩阵的内容。

2. 数据标准化

% 假设所有指标都是正向指标（越大越好）
data_normalized = (data - min(data)) ./ (max(data) - min(data));
% 如果存在负向指标，可以使用以下标准化方法：
% data_normalized = (max(data) - data) ./ (max(data) - min(data));
disp('标准化后的数据矩阵:');
disp(data_normalized);

数据标准化的目的是将不同量纲的数据转化为无量纲的相对值，便于后续计算。

3. 计算比重

p = data_normalized ./ sum(data_normalized);

比重是指每个数据点在总和中的占比。
sum(data_normalized) 计算每列的总和，./ 是按元素进行除法运算。
p 是一个矩阵，表示每个数据点的比重。

4. 计算熵值

k = 1 / log(n); % 归一化系数
e = -k * sum(p .* log(p + eps)); % 加 eps 避免 log(0) 的情况

熵值法用于衡量指标的离散程度，熵值越小，指标的离散程度越大。
k 是归一化系数，用于将熵值归一化到 [0, 1] 范围内。
eps 是一个极小的正数，用于避免 log(0) 的情况。
p .* log(p + eps) 是按元素计算 p 的对数，然后与 p 相乘。
sum(p .* log(p + eps)) 计算每列的总和，得到熵值 e。

5. 计算差异系数

d = 1 - e;

差异系数 d 是熵值的补数，表示指标的差异程度。
差异系数越大，指标的权重越高。

6. 计算权重

weights = d / sum(d);
disp('各指标的权重:');
disp(weights);

权重是通过差异系数归一化得到的。
sum(d) 计算差异系数的总和，d / sum(d) 将差异系数归一化为权重。
weights 是一个向量，表示每个指标的权重。

3.优劣解距离法（VIKOR方法）

优劣解距离法（即 VIKOR方法）是一种用于解决多标准决策问题的工具，核心思路是通过量化每个方案与“理想最优解”和“最劣解”的距离，选出最接近理想、同时最远离最差的“妥协方案”。它的名字来源于其核心思想：既要追求“优”（靠近理想），又要规避“劣”（远离最差），在矛盾目标之间找到平衡。

核心原理类比

假设你要买手机，有3款候选（A、B、C），需从价格、电池、摄像头、内存4个维度对比。你的理想手机是：价格最低、电池最大、摄像头最好、内存最高——但这在现实中几乎不可能同时满足。此时，VIKOR方法会帮你：

定义理想最优解（各指标的最优值组合）和最劣解（各指标的最差值组合）。
计算每款手机与理想解的距离（如价格比理想贵多少），以及与最劣解的距离（如电池比最差好多少）。
综合两种距离，选出最接近理想且远离最劣的“妥协款”——可能不是全优，但综合性价比最高。

关键步骤拆解

设定理想与最劣解
- 理想解：每个指标的最优值（如价格最低、电池最大等）。
- 最劣解：每个指标的最差值（如价格最高、电池最小等）。
标准化数据
消除不同指标的量纲差异（例如，价格是越小越好，电池是越大越好），将所有数值压缩到[0,1]区间。

优化模型

线性优化

1. 基本结构

线性优化模型包含三个要素：

目标函数：需要最大化或最小化的线性表达式。例如企业利润最大化，或运输成本最小化。
约束条件：用线性等式或不等式表示的资源限制。例如机器的工作时间上限、原材料用量限制等。
变量非负性：决策变量（如生产量、投资金额）通常不能为负数。

例如，一家工厂用两种机器生产两种产品，目标是利润最大化。机器使用时间有限制，每种产品需要不同机器工时，这些条件就构成约束。

非线性优化

1.非线性优化的核心是找到满足约束条件下使目标函数最小（或最大）的变量值。

非线性优化是一种数学方法，用于在目标函数或约束条件包含非线性关系时，寻找最优解（如最小值或最大值）。

2.1非线性优化案例
某化工厂生产一种化学品，该化学品的产量取决于反应器中的温度T和压力P。已知:①化学品的产量Y与温度T和压力P的关系为非线性函数:Y(T,P)=10.T.P-2.T-0.1.P
学
②反应器的操作范围限制:温度 T 的范围:100 ≤T<300(单位:℃)压力P的范围:1≤P≤10(单位:MPa)③生产成本与温度和压力的关系为:
Cost(T.P)=5.T+10·P
EHO
④工厂希望在满足操作范围限制的条件下，最大化利润。利润定义为产量减去成本:
ProÃt(T, P)=Y(T, P)-Cost(T,P)

% 定义变量
T = optimvar('T', 'LowerBound', 100, 'UpperBound', 300); % 温度范围
P = optimvar('P', 'LowerBound', 1, 'UpperBound', 10);    % 压力范围

% 定义目标函数
Y = 10*T*P - 2*T^2 - 0.1*P^2; % 产量
Cost = 5*T + 10*P;             % 成本
Profit = Y - Cost;             % 利润

% 创建优化问题
prob = optimproblem('Objective', -Profit); % 因为 fmincon 是最小化，所以取负值

% 设置初始猜测
x0.T = 200; % 初始温度猜测
x0.P = 5;   % 初始压力猜测

% 求解优化问题
[sol, fval] = solve(prob, x0);

% 显示结果
disp(sol);
disp('最大利润: ' + (-fval));

多目标优化

多目标优化在数学建模中是指同时考虑多个相互冲突的目标，并寻找一组能在这些目标之间达成最佳平衡的解决方案。通俗来说，当一个问题需要满足多个“好坏标准”时，无法只追求单一目标的最优，而需在不同目标间妥协，找到综合最优的方案。

数学建模的关键步骤

目标函数与决策变量：明确需优化的多个目标（如经济效益、资源利用率），并将其量化为数学表达式。
约束条件：定义决策变量的可行域，例如物理限制、资源限制等。
模型选择：根据问题特性选择线性/非线性规划、整数规划等模型。

3. 解集特性：Pareto最优性

多目标优化的解集称为Pareto最优解集，即无法通过调整决策变量使某一目标优化而不牺牲其他目标。这些解在目标空间中形成Pareto前沿，反映了目标间的权衡关系。例如，选修课程时需在“课程数量最少”与“学分最高”之间权衡。

4. 求解方法

权重法：将多目标加权求和转化为单目标问题，但需主观确定权重，可能忽略解的多样性。
进化算法：如遗传算法（NSGA-II）、多目标蚁狮优化等，通过种群搜索生成Pareto前沿，适合复杂非线性问题。
目标规划法：如MATLAB中的fgoalattain函数，通过设定目标值进行逼近。

5. 应用领域

多目标优化广泛应用于：

工程设计：如机械结构优化（体积与效率）、控制系统设计。
资源管理：能源分配（效率与成本）、物流路径规划（成本与时间）。
经济与金融：投资组合优化（收益与风险）。

遗传算法

遗传算法（Genetic Algorithm, GA）是一种基于自然选择和遗传学原理的优化技术，广泛应用于数学建模中。它通过模拟生物进化过程中的选择、交叉和变异等操作，逐步优化问题的解，最终逼近全局最优解或准最优解。

在数学建模中，遗传算法主要用于解决复杂优化问题，例如非线性方程组、多目标优化、路径规划等。其核心思想是将问题的解表示为染色体（个体），并利用适应度函数评估每个个体的优劣。通过选择、交叉和变异等操作，不断迭代优化种群，从而逐步逼近最优解

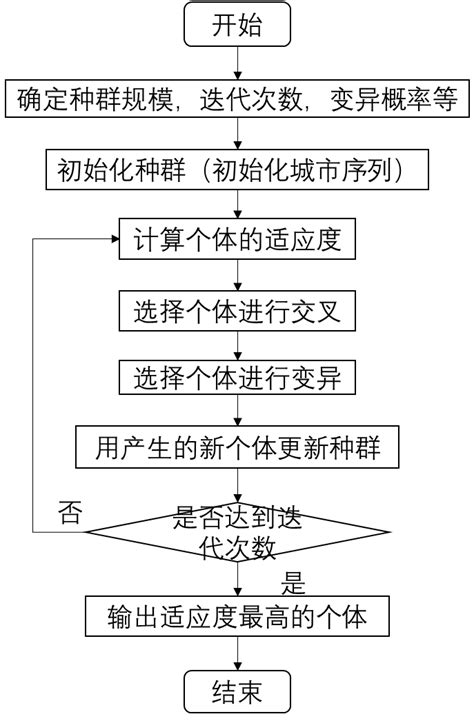
遗传算法具有自组织、自适应和自学习性，可以根据问题特点动态调整参数，如选择策略、交叉概率和变异概率等，从而提高求解性能。

然而，遗传算法也存在一些局限性，如容易陷入局部最优解、收敛速度较慢等。

模拟退火算法

模拟退火算法（Simulated Annealing，简称SA）是一种启发式全局优化算法，其灵感来源于固体物理中的退火过程。在数学建模中，模拟退火算法被广泛应用于解决复杂的优化问题，包括组合优化问题、函数优化问题以及参数优化问题等。其核心思想是通过模拟固体在高温下逐渐冷却的过程，逐步降低系统的能量，从而找到全局最优解或近似最优解。

模拟退火算法的基本原理：

初始状态与温度设置：算法从一个初始解 x0x0 开始，并设定一个初始温度 T0T0。温度 TT 类似于物理中的温度，控制算法的探索范围和接受劣解的概率。
状态转移与接受准则：在每一步迭代中，算法通过随机扰动生成新的解 x′x′，并计算目标函数值的变化 ΔE=f(x′)−f(x)ΔE=f(x′)−f(x)。如果新解的目标函数值更优（即 ΔE≤0ΔE≤0），则直接接受新解；如果新解的目标函数值较差（即 ΔE>0ΔE>0），则以概率 P(ΔE,T)=e−ΔE/(kT)P(ΔE,T)=e−ΔE/(kT) 接受新解，其中 kk 是波尔兹曼常数，TT 是当前温度。
温度下降策略：随着迭代次数的增加，逐步降低温度（如按指数方式 Tnew=αToldTnew=αTold，其中 α<1α<1），使算法逐渐收敛到全局最优解。
终止条件：当连续若干个新解未被接受，或者温度降至某一预设值时，算法终止。

模拟退火算法的特点：

跳出局部最优解的能力：通过Metropolis准则，算法允许在一定概率下接受劣解，从而避免陷入局部最优解。
全局搜索能力：由于温度逐渐下降，算法能够在较大的搜索空间中进行全局搜索，最终趋向于全局最优解。
适用范围广：模拟退火算法适用于解决NP-hard问题、组合优化问题以及复杂的非凸优化问题。

模拟退火算法的实现步骤：

初始化：设定初始解、初始温度和降温系数。
生成新解并计算目标函数差值。
判断是否接受新解（基于Metropolis准则）。
更新当前解和温度。
检查终止条件，若满足则结束；否则返回步骤2

预测模型

ARIMA

（AutoRegressive Integrated Moving Average，自回归积分滑动平均模型）是一种经典的时间序列预测方法，主要用于处理非平稳数据，通过对数据进行差分使其平稳化后再建模。以下是其核心要点：

自回归（AR）、差分（I）和移动平均（MA）

工作原理

平稳化处理：通过差分（I）消除时间序列的趋势和季节性，使其满足平稳性要求（如均值、方差恒定）。ADF检验常用于验证序列是否平稳。
自回归（AR）部分：利用历史值的线性组合预测未来值，例如：
xt=ϕ1xt−1+ϕ2xt−2+⋯+ϕpxt−p+ϵtxt=ϕ1xt−1+ϕ2xt−2+⋯+ϕpxt−p+ϵt，其中ϕ为自回归系数。
移动平均（MA）部分：结合历史预测误差优化模型，例如：
xt=ϵt−θ1ϵt−1−⋯−θqϵt−qxt=ϵt−θ1ϵt−1−⋯−θqϵt−q，其中θ为移动平均系数。
整合（ARMA） ：将差分后的平稳序列用ARMA(p, q)建模，最终形成ARIMA模型。

建模步骤：

序列平稳化：通过差分（d阶）处理非平稳数据。
参数选择：利用自相关函数（ACF）和偏自相关函数（PACF）图识别p和q，或通过信息准则（如AIC、BIC）自动选择。
模型拟合与验证：采用最大似然估计或最小二乘法估计参数，并通过残差分析（如Ljung-Box检验）检验模型有效性。

应用与优缺点

应用场景：适用于短期预测，广泛应用于经济（如CPI预测）、气象、能源等领域。
优点：解释性强，适合线性关系明显且平稳/可差分的数据。
局限性：对非线性关系（如突变事件）处理能力较弱，长期预测精度下降。

马尔科夫预测

一种基于马尔科夫链原理的统计模型，其核心假设是系统未来状态仅依赖于当前状态，与过去历史状态无关，这一特性被称为“马氏性”或“无后效性”。以下是关于该模型的详细解析：

建模步骤：

确定状态空间：根据问题特点划分可能的状态集合（如将降水量分为“丰水”“平水”“枯水”状态）。
计算状态转移概率：通过历史数据统计各状态间的转移频率，构建转移概率矩阵。
初始状态概率：定义系统的初始状态分布。
递推预测：利用转移矩阵和初始概率，通过矩阵乘法递推未来各时刻的状态概率分布

优点：
- 简化复杂性：仅依赖当前状态，减少历史数据处理的计算量。
- 适应随机性：对波动性数据（如金融市场、气象变化）有较好的短期预测效果。
- 灵活扩展：可与其他模型（如灰色模型、神经网络）结合，提升预测精度。
缺点：
- 长期预测局限性：转移概率固定，无法反映长期趋势变化，易产生误差累积。
- 状态划分依赖：状态划分的合理性直接影响预测效果，需结合领域知识调整。
- 数据要求严格：需足够的历史数据统计转移概率，否则可能导致矩阵稀疏

马尔科夫预测模型在数学建模中是一种高效的工具，尤其适合短期随机性预测问题。其核心在于利用状态转移矩阵量化系统动态，但需注意状态划分的合理性和长期预测的局限性。

灰色预测模型

灰色预测模型是数学建模中一种处理不完全信息或不确定数据的预测方法，其核心思想是通过少量、不完整的原始数据揭示系统内在规律，进而预测未来趋势。

核心特点与适用场景

数据需求低：适用于小样本（如短时间序列）或数据质量较差的情况。
处理不确定性：通过灰色生成（如累加、累减、均值生成）减弱数据随机性，将原始数据转化为规律性更强的序列。
短期预测优势：尤其在非线性、非平稳系统中表现突出，常用于短期趋势分析

建模流程

数据预处理：检验原始数据级比，通过累加生成新序列（如将 x(0) 转化为 x(1)）。
构建微分方程：建立白化方程描述系统动态，例如GM(1,1)的微分方程形式。
参数求解与预测：利用最小二乘法确定发展系数 aa 和灰色作用量 uu，求解时间响应函数得到预测值。
模型检验：包括残差检验、后验差检验、关联度分析等，评估模型精度

灰色预测模型通过“部分已知信息”揭示系统整体规律，是数学建模中处理不确定性问题的利器，尤其在小样本、短期预测场景中具有不可替代性。其核心在于通过数据生成与微分方程建模，将灰色信息“白化”，为决策提供科学依据。

统计模型

1.相关分析

1.1 Pearson相关系数原理

Pearson相关系数（Pearson correlation coefficient）是一种衡量两个变量之间线性相关程度的统计指标，其核心原理是通过协方差与标准差的比值来量化变量间的关联强度。

其中，分子是两变量的协方差，分母是各自标准差的乘积。

协方差：反映两个变量同时偏离均值的程度。若两者同方向偏离（如一个高于均值时另一个也高），协方差为正；反之则为负。

标准化：通过除以标准差，将协方差缩放到-1到1之间，消除量纲影响，使结果更可比。

取值范围与意义

-1到1之间：
- r=1：完全正相关，变量呈严格递增的直线关系。
- r=-1：完全负相关，变量呈严格递减的直线关系。
- r=0：无线性相关，但可能有其他非线性关系（如曲线相关）。
绝对值大小：越接近1，线性关系越强。例如，r=0.8表示强正相关，r=0.3表示弱相关

1.2spearman相关系数

Spearman相关系数用于衡量两个变量之间的单调关系强度，即无论两者的关系是直线还是曲线，只要一个变量增加时另一个变量也倾向于增加（或减少），就能检测到相关性。它通过将原始数据转换为排名（如第一名、第二名等）来计算相关性，关注的是变量间的相对位置变化是否一致

何时用Spearman：数据非正态、含异常值、为有序变量或关系单调但非线性时。

何时用Pearson：数据正态分布、关系明确为线性且无异常值干扰时。

注意：相关系数仅反映统计关联，不能证明因果关系

Spearman 相关系数优缺点优点:
1.不要求数据服从正态分布

2.对异常值不敏感

3.能捕捉单调关系(线性或非线性）

缺点:·对非单调关系(如周期性关系)不敏感
计算复杂度略高于Pearson相关系数

2.回归模型

2.1回归方程设定

模型类型

根据数据特点，回归模型可分为多种类型：

1.线性回归：变量间呈直线关系，如 Y=β0+β1xY，适用于简单因果关系分析。

2.非线性回归：如对数模型 y=A+Bln⁡x、指数模型 y=AeBx，用于曲线关系的数据拟合。

模型整体显著性检验（F检验）

原假设设定
检验所有自变量对因变量无显著影响，即原假设为 H0:β1=β2=⋯=βm=0所有回归系数为零）。
统计量构造
通过方差分析（ANOVA）分解总平方和（SST）为回归平方和（SSR）和残差平方和（SSE），构造F统计量：

F=SSR/mSSE/(n−m−1)∼F(m,n−m−1)

其中 mm 为自变量个数，nn 为样本量
决策规则
若计算出的F值大于临界值 Fα(m,n−m−1)Fα(m,n−m−1)，或p值小于显著性水平（如0.05），则拒绝原假设，认为模型整体显著。

3.聚类模型

聚类模型是一种无监督学习方法，旨在将数据集划分为若干内部相似性高、类间差异大的组别。

3.1 K-means聚类

步骤：
1. 选择初始聚类中心（可优化为K-means++算法以减少初始敏感度）。
2. 迭代更新中心点：将样本分配至最近中心，重新计算中心坐标。
3. 重复直至准则函数（如误差平方和）收敛。
特点：计算高效，但对噪声敏感，需预先指定簇数 kk。

核心原理

“物以类聚” ：假设要将数据分为 K 类（如 K=3），算法会先随机选 K 个点作为“临时中心”，然后根据数据点到这些中心的距离进行归类（距离最近的为一类）。接着重新计算每个类的中心（取均值），并重复这一过程，直到中心点不再变化或达到最大迭代次数。
数学目标：最小化簇内数据到中心的距离平方和（即簇内越紧密越好）。

2. 具体步骤

确定 K 值：需人工指定要分几类（如 K=2、3 等）。这是算法的关键难点，常用“肘部法”辅助选择。
随机初始化中心：随机选 K 个数据点作为初始中心。
分配数据点：计算所有点到 K 个中心的距离（如欧氏距离），将每个点归入最近的中心所在簇。
更新中心位置：计算每个簇的均值点作为新中心。
重复迭代：重复步骤 3-4，直到中心点不再变化或达到预设的迭代次数。

3. 优缺点

优点：
- 简单易懂，计算效率高，适合大规模数据。
- 结果直观，适用于客户分群、图像压缩、异常检测等场景。
缺点：
- 需预先指定 K 值，选择不当可能导致效果差。
- 对初始中心敏感，不同初始值可能得到不同结果。
- 对噪声和离群点敏感，且难以处理非球形簇或大小差异大的簇

K-means 像是一种“自动分组工具”，通过不断优化中心位置实现数据的自然聚类，但需人工干预 K 值和初始设置，适用于结构相对清晰的数据集。

3.2系统聚类法（也称层次聚类法）

是一种基于“逐步合并”思想的聚类方法，其核心是将数据从“最分散”到“最聚合”的过程以树状图（谱系图）的形式展示，帮助用户直观选择分类数量。以下是通俗解释：

基本思想

初始状态：每个样本单独成一类。例如，若有10个样本，则初始有10个类，每个类仅包含1个样本。
逐步合并：计算所有类之间的距离，将距离最近的两类合并为一个新类。例如，若样本A和B的距离最近，则合并为类AB。
重复合并：更新类间距离后，继续合并最接近的类，直到所有样本最终合并为一个大类。
结果展示：整个过程形成一棵“倒置的树”（谱系图），用户可根据需求在树的某一层“切断”，决定最终分类数。

关键步骤

计算距离：
- 初始时计算所有样本两两之间的距离（如欧式距离、绝对值距离等）。
- 合并后需重新计算新类与其他类的距离。例如，若用“最短距离法”，新类AB与类C的距离取AB中与C最近的单一样本的距离。
合并规则：
- 每次只合并距离最小的两类，直到所有类聚合完毕。
可视化工具：
- 谱系图（树状图）展示合并顺序，纵轴表示类间距离，横轴为样本。通过观察距离突变点（类似“手肘法”）确定合理分类数。

特点与适用场景

优点：
- 无需预先指定分类数，适合探索性分析。
- 结果直观，谱系图可展示多种分类可能性。
缺点：
- 计算量大，尤其样本多时效率低。
- 对高维数据敏感，需谨慎选择距离度量方式。

系统聚类法像“搭积木”：从最底层的小积木（单一样本）开始，逐步将最相似的积木拼合，最终形成完整的结构，用户可根据需求选择拼合的中间状态作为分类结果。

3.3 谱聚类

是一种基于图论和线性代数的聚类方法，其核心思想是将数据点转化为图中的节点，利用节点之间的相似性进行分组。

具体步骤

构建相似性图
- 将每个数据点看作图中的一个节点，通过计算点与点之间的相似性（如高斯核函数、欧氏距离等）生成邻接矩阵（即相似性矩阵）。例如，邻接矩阵中的元素 WijWij 表示第 ii 个点和第 jj 个点的相似度。
构造拉普拉斯矩阵
- 根据邻接矩阵计算度矩阵（对角线元素为每个节点的总连接强度，即边的权重之和），再生成拉普拉斯矩阵（通常为 L=D−WL=D−W，其中 DD 是度矩阵，WW 是邻接矩阵）。这一步的关键在于将图的结构转化为数学对象，便于后续分析。
特征分解与降维
- 对拉普拉斯矩阵进行特征分解，选取前 kk 个最小的非零特征值对应的特征向量（kk 为目标聚类数）。这些特征向量将原始数据从高维空间映射到低维空间，使得原本复杂的数据结构在低维空间中更容易被划分。
执行传统聚类
- 在低维空间中，使用简单的聚类算法（如K-means）对特征向量进行分组。例如，将每个数据点对应的特征向量视为新的坐标，再对这些坐标进行聚类.

优势与适用场景

处理复杂形状
- 传统K-means只能划分球形簇，而谱聚类可处理任意形状（如环形、交叉分布）的数据。
高维数据友好
- 仅需相似性矩阵，不依赖数据的具体坐标形式，适合文本、图像等高维数据。
抗噪性强
- 通过特征向量降维时，能忽略次要噪声，抓住主要结构。

谱聚类的核心是通过图的结构分析和矩阵降维，将复杂问题转化为简单聚类任务。其步骤可概括为：构建图→数学建模→降维→聚类。这种方法灵活且强大，尤其适合传统聚类算法难以处理的数据结构。

微分方程模型

Logistic增长模型

一种用于描述有限资源环境下种群或现象增长的经典工具。

Logistic模型由比利时数学家Pierre-François Verhulst于1838年提出，作为马尔萨斯指数增长模型的改进。其基本微分方程为：

其中：

y(t)表示时间tt时的种群规模或现象量值；
r为内在增长率（r>0）；
K为环境容纳量（Carrying Capacity），即资源限制下的最大可持续规模。

该方程的解为Logistic函数：

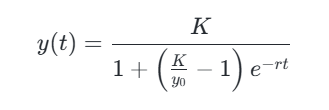
其中y0y0为初始值。其曲线呈现典型的S型特征：

初始阶段：增长近似指数（y≪Ky≪K时，1−y/K≈11−y/K≈1）；
加速阶段：增速逐渐达到峰值（拐点位于y=K/2处）；
饱和阶段：接近KK时增速趋近于零，最终稳定在容纳量附近。

Lotka-Volterra模型（简称LV模型）

是数学建模中用于描述两个物种（通常是捕食者与猎物）动态相互作用的基础工具，其核心为一组非线性常微分方程。

LV模型由Alfred Lotka和Vito Volterra独立提出，基本形式为：

x,y分别表示猎物和捕食者的种群数量。
参数 α（猎物增长率）、β（猎物被捕食率）、γ(捕食者死亡率）、δ（捕食效率）控制动态平衡。
模型预测两种平衡态：灭绝态与共存态，并展现周期性振荡特性.

matlab的基础知识

1.matlab赋值语句：

a = 10;
a = 2

分号的作用：在赋值语句的末尾加上分号（;）会抑制输出，即不会在命令窗口显示赋值结果。如果不加分号，MATLAB 会自动将赋值结果输出到命令窗口。

2.多行注释，快捷键Ctrl+R , 使用 %{ ... %} 块注释语法

% a = 10;

3.取消注释，快捷键 Ctrl+T

4.清除工作区的所有变量 clear , 清除命令框的 clc

5.输出和输入函数（disp和input)

6.判断语句

多分支 if-elseif-else 语句

x = 10;

if x > 0
disp('x 是正数');
elseif x < 0
disp('x 是负数');
else
disp('x 是零');
end

switch-case 语句用于根据变量的值选择执行不同的代码块。

day = 3;

switch day
    case 1
        disp('星期一');
    case 2
        disp('星期二');
    case 3
        disp('星期三');
    case 4
        disp('星期四');
    case 5
        disp('星期五');
    otherwise
        disp('周末');
end

7.sum求和函数

示例 1：向量求和

v = [1, 2, 3, 4, 5];
S = sum(v); % 返回所有元素的和
disp(S); % 输出 15

示例 2：矩阵求和（按列求和）

A = [1, 2, 3; 4, 5, 6];
S = sum(A); % 返回每一列的和
disp(S); % 输出 [5, 7, 9]

示例 3：矩阵求和（按行求和）

A = [1, 2, 3; 4, 5, 6];
S = sum(A, 2); % 按行求和
disp(S); % 输出 [6; 15]

示例 4：多维数组求和

B = rand(2, 3, 2); % 创建一个 2x3x2 的随机数组
S = sum(B, 3); % 沿着第三个维度求和
disp(S); % 输出一个 2x3 的矩阵

示例 5：对整个数组求和

A = [1, 2, 3; 4, 5, 6];
S = sum(A, 'all'); % 对整个数组的所有元素求和
disp(S); % 输出 21

示例 6：忽略 NaN 值

A = [1, 2, NaN; 4, NaN, 6];
S = sum(A, 'omitnan'); % 忽略 NaN 值后求和
disp(S); % 输出 [5, 2, 6]

8.size函数

示例 1：获取矩阵的尺寸

A = [1, 2, 3; 4, 5, 6];
d = size(A); % 返回矩阵的尺寸
disp(d); % 输出 [2, 3]，表示矩阵有 2 行 3 列

示例 2：分别获取行数和列数

A = [1, 2, 3; 4, 5, 6];
[rows, cols] = size(A); % 分别获取行数和列数
disp(['行数：', num2str(rows)]); % 输出 行数：2
disp(['列数：', num2str(cols)]); % 输出 列数：3

9.repmat 函数

用于将一个数组或矩阵重复排列成一个更大的数组。它的名字来源于 “repeat matrix”，即重复矩阵。

示例 1：重复二维矩阵

A = [1, 2; 3, 4];
B = repmat(A, 2, 3); % 将 A 在行方向重复 2 次，在列方向重复 3 次
disp(B);

输出结果：

     1     2     1     2     1     2
     3     4     3     4     3     4
     1     2     1     2     1     2
     3     4     3     4     3     4

10.导入excel表格数据.

数据异常值怎么处理

x = 1:100;  % 构造一个数组，元素为 1，2，3，……，100
% randn(1,100) 意味着生成一个 1 行 100 列的矩阵
% 矩阵元素的均值为 0，方差 σ^2 = 1，且是正态分布的随机数
data = randn(1,100);
data(20:20:80) = NaN;  % 设置第 20，40，60，80 个元素为缺失值
% data 的值都是在 0 附近的，设置 4 个异常值
data(10) = -50;
data(40) = 45;
data(70) = -40;
data(90) = 50;
plot(x,data)

关于写论文的技巧

查文献的技巧

1.先看知网的硕博士论文
        硕博论文会对研究的问题有详细的背景和基础知识介绍，可帮助我们快速理解题目按照“被引”排序。
2.高级检索:想了解神经网络在信贷策略中的应用，想找一些相关的硕博论文
        1.进入高级检索界面，+ ”和“-”可以自定义增加和减少检索字段
2.主题为:企业信贷
        3.OR 主题为:信贷决策
        4.AND 关键词:神经网络，词频设置为“模糊”。模糊”是输入的检索词在检索结果中出现即可，字序字间间隔可以产生变化。

查文献的网站：

1.知网：中国知网

2.Open Access Library (OALib)

查数据的技巧

1.知网，谷歌学术。

2.国家数据：国家数据。

数据预处理

1.缺失值（null)

简单的处理：

1.均值和众值插补：对精度要求不大的数据。

2.newton插值法：一种通过构造多项式来逼近给定数据点的数值插值方法，适用于通过 n+1n+1 个数据点生成 nn 阶多项式。其核心思想是利用差商（divided differences）逐步构建插值多项式，具有递推性和高效计算的特点。

3.样条插值法：一种通过分段低阶多项式来平滑连接多个数据点的数学方法。通俗来说，它就像用多段“小曲线”拼接成一条整体平滑的曲线，每段曲线仅覆盖相邻两个数据点之间的区域，且连接处过渡自然，不会出现突兀的折角或震荡。

2.异常值

“距离法” ：假设数据大致服从正态分布时，若某个值与平均值的距离超过3倍标准差（即3σ原则），则视为异常值。例如，全班数学成绩平均70分，标准差10分，那么超过100分（70+3×10）或低于40分（70-3×10）的分数可能是异常值。

论文的整体排版

各级标题与正文层次分明
1.一般标题级别不超过三级，
2.正文中文字体设置宋体、英文Times New Roman
3.正文排版紧凑，看起来充实，没有大片空白。避免图片过大导致出现大片空白，且不要留有空行
表格与图片
4.表格用标准的三线表。

5.表的标题放在表的上方，图名放在图的下方
6.公式编辑：推荐mathpix，或用word的公式编辑器.

7.文字要分段。

论文标题怎么写

基于kxx模型的xxx问题研究，读完标题，就能知道本文建的是什么模型，简明扼要、符合规范、便于检索，尽量使用大家都知道的词语，避免出现公式、非公知公用的缩写，字数限制在一行内。
xxx问题就是赛题的中心词
不要使用过多的修饰词
基于一维热传导方程的炉温曲线机理问题研究
基于单目标优化模型的CT系统成像问题研究
基于多目标优化模型的系泊系统问题研究
基于动态规划补贴的出租车资源匹配问题研究
基于差分方程和元胞自动机的交通阻塞问题研究
基于回归分析的长江水质预测问题研究

论文的摘要怎么写

口摘要是重中之重!!!!!
基本要求：
1.摘要是对论文的概括总结 2.让评阅老师读完摘要，就知道本文解决的问题，建立的模型和求解结果。
注意事项·不要加图或表格字数大约800~1100控制在3/4页到一页，
开头段:本文针对XXX问题，通过建立XXX模型，实现对XXX的求解。
针对问题一，建立XXX模型/利用XXX方法,，…..求解出XXX
针对问题二，建立XXX模型/利用XXX方法.求解出XXX。
针对问题三，考虑XXX，...求解出XXX。建立XXX模型/利用XXX方法。。”
总结:总结全文，继而分析下你用的模型的优点，自夸一下。
关键词:主要模型/算法，或出现频率高的、体现论文针对的问题的词。