【51单片机】51单片机最小系统的组成以及原理图

概述

51单片机是一种非常常用的单片机，其应用范围广泛。在学习和使用51单片机时，最小系统是必不可少的。本文将介绍51单片机最小系统的组成和原理。

一、51单片机最小系统组成

        51单片机最小系统是一种基于51单片机的最小化电路系统，它包含了51单片机所需的最少元件，以便实现基本的功能。这种系统通常用于学习和实验目的，使学习者能够在没有复杂电路的情况下快速了解51单片机的工作原理。

        而51单片机最小系统分别由时钟电路、复位电路、供电电路组成。

        51最小系统结构框图如下所示：

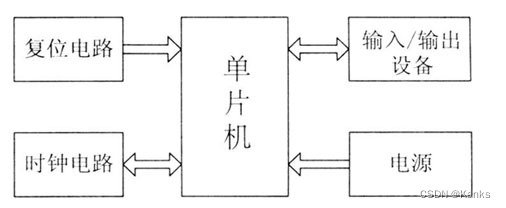
      时钟电路

        单片机是一个复杂的同步时序电路，为了保证同步工作方式的实现，电路应在唯一的时钟信号控制下严格地按时序进行工作。时钟电路用于产生单片机工作所需要的时钟信号。

       1.时钟信号的产生

        在51单片机内部有一个高增益反相放大器，其输入端引脚为XTAL1，其输出端引脚为XTAL2。只要在XTAL1和XTAL2之间跨接晶体振荡器和微调电容，就可以构成一个稳定的自激振荡器。  

        2.时序

        关于51单盘及的时序概念有4个，可用定时单位来说明，从小到大依次是：节拍、状态、机器周期和指令周期，下面分别加以说明。

        1）节拍

        把振荡脉冲的周期定义为节拍，用P表示，也就是晶振的振荡频率。

        2）状态

        振荡脉冲经过二分频后，就是单片机时钟信号的周期，定义为状态，用S表示。一个状态包含两个节拍，其前半周期对应的节拍称为P1，后半周期对应的节拍称为P2。

        3）机器周期

        51单片机采用定时控制方式，有固定的机器周期。规定一个机器周期的宽度为6个状态，即12个振荡脉冲周期，因此机器周期就是振荡脉冲的十二分频。

        4）指令周期

        指令周期是最大的时序定时定位，将执行一条指令所需要的时间称为指令周期。它一般由若干个机器周期组成。不同的指令，所需要的机器周期数也不同。通常，将包含一个机器周期的指令称为单周期指令，包含两个机器周期的指令称为双周期指令，依次类推。

      复位电路

        复位电路，就是利用它把电路恢复到起始状态。就像计算器的清零按钮的作用一样，以便回到原始状态，重新进行计算。和计算器清零按钮有所不同的是，复位电路启动的手段有所不同。一是在给电路通电时马_上进行复位操作;二是在必要时可以由手动操作;三是根据程序或者电路运行的需要自动地进行。

       1.单片机复位的条件

        必须使RST（第9引脚）加上持续两个机器周期（即24个脉冲振荡周期）以上的高电平。若时钟频率为12MHz，每个机器周期为1μs，则需要加上持续2μs以上时间的高电平。

       2.单片机常见的复位电路

        1）上电复位电路：利用电容充电来实现复位，在接电瞬间，RST端的电位与Vcc相同，随着充电电流的减少，RST的电位逐渐下降。只要保证RST为高电平的时间大于两个机器周期，使能正常复位。

        2）按键复位电路：是一种电子电路，用于实现设备的复位功能。当设备出现故障或需要重新启动时，通过按下复位按键，使设备恢复到正常工作状态。

      供电电路

        51单片机最小系统电路中的供电电路需要提供稳定的电压给单片机进行正常的工作。具体来说，它包括一个电源模块，将输入的交流电转化为直流电供给单片机使用。此外，还需要加入滤波电容等元件来稳定电源波动，避免对单片机的工作产生影响。具体的电路设计和元件选择需要根据实际应用场景和需求来进行。

二、51单片机最小系统原理图

这里使用Proteus作为仿真软件、AT89C52作为芯片绘制了原理图：

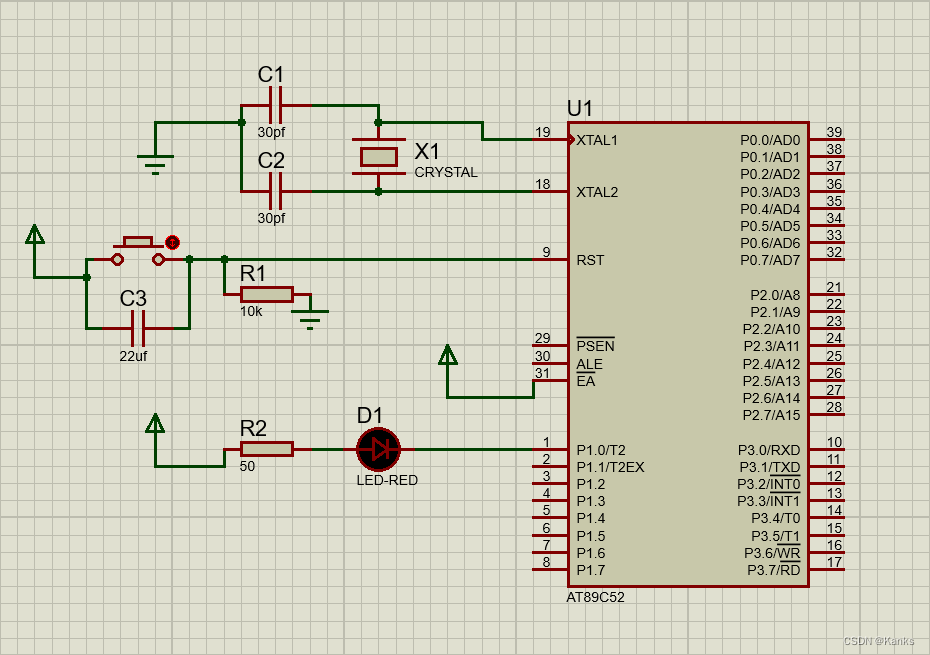
1）时钟电路：使用到了两个30pf的电解电容和晶振

2）复位电路：用到了22μf电解电容、10k电阻、按钮开关

此处为按键复位电路

 3）供电电路：用到了电阻、LED灯

三、总结      

       最小系统的应用十分广泛，可以应用于各种电子设备和嵌入式系统中，如工业控制、汽车电子、家用电器、智能家居等等。通过最小系统，可以方便地学习、测试和应用单片机。

基于51单片机的智能小车：

自动化生产线上常见的AGV小车：

       总之，最小系统是单片机应用开发的基础，掌握最小系统的基本原理和设计方法对进一步学习单片机具有非常重要的意义。在实际应用中，需要根据具体的应用场景和需求来进行设计和优化，确保系统的可靠性和稳定性。