探索：斯坦纳树

C++斯坦纳树（C++ Steiner Tree）是一种用于解决图论问题的算法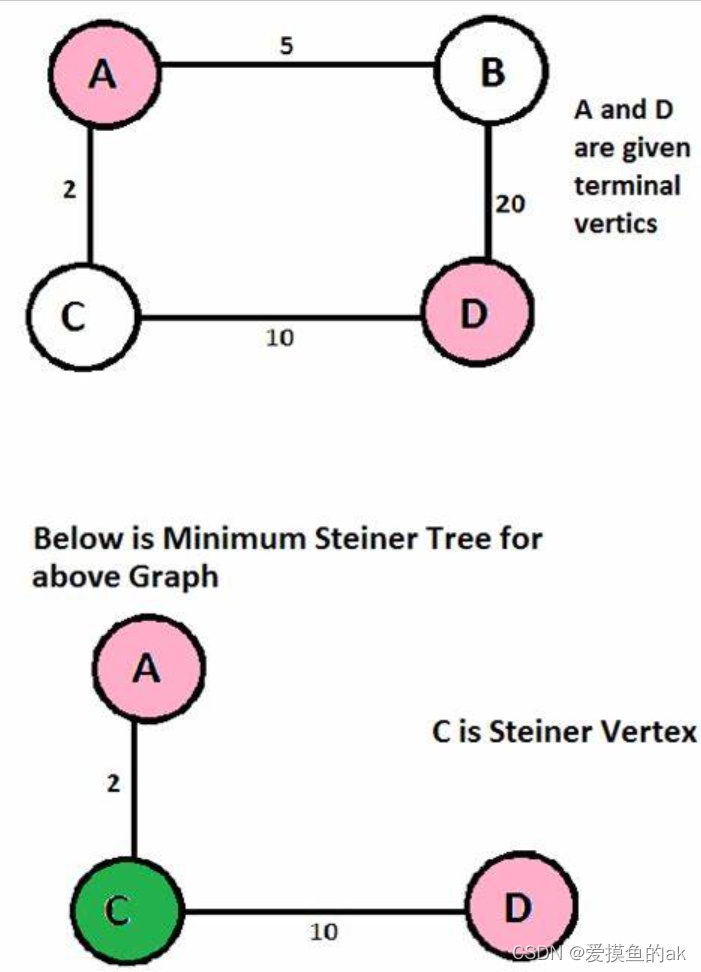。斯坦纳树是一种最小生成树的扩展，它在一个给定的图中找到一个子集，将所有指定的顶点连接起来，并且总权重最小。

C++斯坦纳树的实现可以通过以下步骤完成：

1. 创建一个图的数据结构，可以使用邻接矩阵或邻接列表表示。

2. 初始化一个二维数组来存储斯坦纳树的权重信息。初始化为无穷大。

3. 对于图中的每一个顶点，使用Dijkstra算法计算该顶点到其他顶点的最短路径，并更新斯坦纳树的权重数组。

4. 对斯坦纳树的权重数组进行修剪，删除不必要的边，以达到最小权重。

5. 输出斯坦纳树的权重信息，以及连接顶点的路径。

C++斯坦纳树的实现可以使用图论的基础数据结构和算法来完成，例如Dijkstra算法和最小生成树的算法。通过使用C++的类和函数，可以更好地组织和管理代码，使实现更加简洁和可读。

在实际应用中，C++斯坦纳树可以用于网络设计、物流规划、电路布局等问题，通过建模成图论问题，使用斯坦纳树算法来找到最优解。

手打实现板子如下：

#include &ltbits/stdc++.h&gt
using namespace std;

const int maxn = 510;
const int INF = 0x3f3f3f3f;
typedef pair&ltint, int&gt Pair;

int n, m, k;
struct Edge {
    int to, next, weight;
} edges[maxn &lt&lt 1];
int head[maxn &lt&lt 1], tree[maxn &lt&lt 1], total;
int dp[maxn][5000], visited[maxn];
int keys[maxn];
priority_queue&ltPair, vector&ltPair&gt, greater&ltPair&gt &gt pq;

void addEdge(int u, int v, int w) {
    edges[++total] = Edge{v, head[u], w};
    head[u] = total;
}

void dijkstra(int source) {
    memset(visited, 0, sizeof(visited));
    while (!pq.empty()) {
        Pair item = pq.top();
        pq.pop();
        if (visited[item.second]) continue;
        visited[item.second] = 1;
        for (int i = head[item.second]; i; i = edges[i].next) {
            if (dp[tree[i]][source] &gt dp[item.second][source] + edges[i].weight) {
                dp[tree[i]][source] = dp[item.second][source] + edges[i].weight;
                pq.push(Pair(dp[tree[i]][source], tree[i]));
            }
        }
    }
}

int main() {
    memset(dp, INF, sizeof(dp));
    scanf("%d %d %d", &n, &m, &k);
    int u, v, w;
    for (int i = 1; i &lt= m; i++) {
        scanf("%d %d %d", &u, &v, &w);
        addEdge(u, v, w);
        tree[total] = v;
        addEdge(v, u, w);
        tree[total] = u;
    }
  
    for (int i = 1; i &lt= k; i++) {
        scanf("%d", &keys[i]);
        dp[keys[i]][1 &lt&lt (i - 1)] = 0;
    }
    
    for (int s = 1; s &lt (1 &lt&lt k); s++) {
        for (int i = 1; i &lt= n; i++) {
            for (int subs = s & (s - 1); subs; subs = s & (subs - 1)) {
                dp[i][s] = min(dp[i][s], dp[i][subs] + dp[i][s ^ subs]);
            }
            if (dp[i][s] != INF) pq.push(Pair(dp[i][s], i));
        }
        dijkstra(s);
    }
    
    printf("%d\n", dp[keys[1]][(1 &lt&lt k) - 1]);
    
    return 0;
}

此代码使用Dijkstra算法和动态规划的求解最短路径的问题。

首先，定义了一个结构体Edge，表示图的边，包括to（边的终点）、next（下一条边的指针）和weight（边的权重）。

然后定义了一些常量和全局变量，包括最大节点数maxn、最大权重INF、节点数n、边数m、关键节点数k、边数组edges、头节点数组head、树节点数组tree、边数total、最短路径数组dp、已访问数组visited和关键节点数组keys。

接下来定义了一个优先队列pq，用于实现Dijkstra算法的优先级队列。

addEdge函数用于将边添加到图中。首先将边信息存入edges数组，并将edges数组中的total位置赋给head数组中的u位置，表示从u节点出发的第一条边的索引。

dijkstra函数用于求解从source节点出发的最短路径。首先将visited数组初始化为0，表示所有节点都未被访问。然后，不断从pq中取出优先级最高的节点 item，如果该节点已被访问，则继续下一轮循环。否则，将该节点标记为已访问，并遍历该节点指向的所有边。如果通过该边可以得到更短的路径，则更新dp数组，并将该节点加入pq。

在主函数中，首先将dp数组初始化为INF，表示所有路径都无穷大。

然后读入节点数n、边数m和关键节点数k，并循环读入每条边的起点u、终点v和权重w。将边添加到图中，并将终点v加入树节点数组tree中。

接下来循环读入每个关键节点keys[i]，并将dp[keys[i]][1<<(i-1)]初始化为0，表示这些节点到自身的路径长度为0。

然后，使用动态规划的方法求解最短路径。循环从1到(1<<k)-1，表示从第一个关键节点到最后一个关键节点的所有路径。在每次循环中，遍历所有节点i，将路径s划分为两部分，分别为s的子集subs和s与subs的差集，然后更新dp[i][s]为dp[i][subs]+dp[i][s^subs]的最小值。如果dp[i][s]不为INF，则将该节点加入pq。

最后输出dp[keys[1]][(1<<k)-1]，即从第一个关键节点到最后一个关键节点的最短路径长度。

整个程序的主要思路是使用动态规划从小到大递推出更大规模的最短路径，然后使用Dijkstra算法从关键节点逐渐扩展到整个图的最短路径。