大数运算——N阶乘（高精度）

上一篇我们已经系统的学习了高精度算法(http://t.csdnimg.cn/9cGaF) 但是光学习不实践必然是枯燥乏味的。现在我们来学习如何使用高精度。

大数运算——N阶乘

阶乘： 是基斯顿·卡曼（Christian Kramp，1760～1826）于 1808 年发明的运算符号，是数学术语。一个正整数的阶乘（factorial）是所有小于及等于该数的正整数的积，并且0的阶乘为1。自然数n的阶乘写作n!。1808年，基斯顿·卡曼引进这个表示法。
亦即n!=1×2×3×…×(n-1)×n。阶乘亦可以递归方式定义：0!=1，n!=(n-1)!×n。
平常遇到需要阶乘时我们大多数会用循环累乘或者函数的递归，但这种方法都是基于开一个变量，这个变量可以是int最大可以是long long但即使用long long变量范围也很有限(不到30！)。由此我们就思考有什么办法能算到更高位的阶乘呢？哎？
上一篇讲到的高精度乘法就能完美解决这个问题。
先用个具体阶乘举例：5！

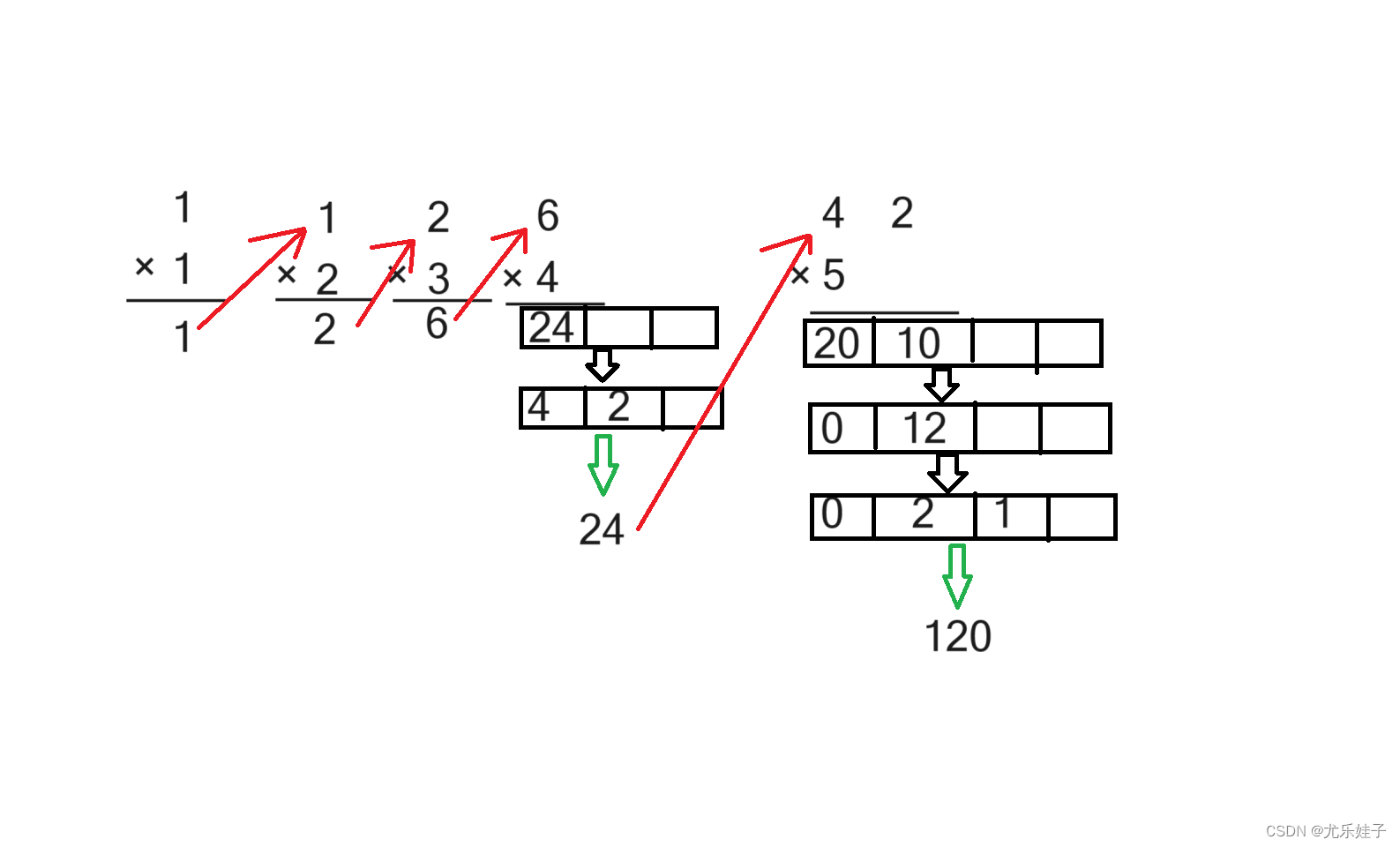
让我们看代码吧~

#include<iostream>
#include<string.h>
using namespace std;
#define h 250000
char print[h] = { '1' };
int num1[h] = { 0 }, num2[h] = { 0 };
void fact(int n)
{
	int ans[h] = { 0 };
	int len1 = 0, sumlen,k = 0;
	len1 = strlen(print);
	//反转写入数组
	for (int i = len1 - 1; i >= 0; i--)num1[k++] = (print[i] - '0');
	k = 0;
	//将因数拆分反向装入数组
	while (n)
	{
		num2[k++] = n % 10;
		n /= 10;
	}
	//模拟乘法竖式
	for (int i = 0; i < len1; i++)
	{
		for (int j = 0; j < k; j++)
		{
			ans[j + i] += num1[i] * num2[j];
		}
	}
	sumlen = len1 + k;
	k = 0;
	//进位
	for (int i = 0; i < sumlen; i++)
	{
		if (ans[i] >= 10)
		{
			ans[i + 1] += ans[i] / 10;
			ans[i] = ans[i] % 10;
		}
	}
	//反转写入字符串
	while (!ans[sumlen])sumlen--;
	for (int i = sumlen; i >= 0; i--)print[k++] = ans[i] + '0';
}
int main()
{
	int n;
	cin >> n;
	for (int i = 1; i <= n; i++)
	{
		fact(i);
	}
	cout << print;
}

核心思想： 将每次在主函数循环传入的数带入到函数中存到num2[]，而num1[]是由每次循环得出结果的print[]传入，通过高精度乘法将num1[]与num2[]算出的结果先存入数组ans[]，再由数组ans[]传入字符串print[]，主函数通过循环反复调用函数fact()实现更新全局变量中的字符串print[]（若为局部变量则会在每次函数结束直接删除）。

• charprint[h]：每次循环计算得出的积都会更新存放到该字符串中。intnum1[h]：用于存放每次print[h]保存的数作为新的因数。num2[h]：存放新的阶乘数作为另一个因数。
• intlen1:计算num1[]字符串的长度。sumlen：用来计算两个因数的位数和(为什么算的是两个因数和呢？答：参考高精度乘法中maxlen)。k=0：数组起始下标。
• num1[]反转写入数组：
  for (int i = len1 - 1; i >= 0; i--)num1[k++] = (print[i] - '0');在上一篇已经具体讲解过为什么要反转了（为了要逐位对齐），不同的是这次是直接反转写入数组中。
• num2[]反转写入数组：

while (n)
	{
		num2[k++] = n % 10;
		n /= 10;
	}

一个整数的反转逐位写入数组的方法就是将自身摩除(%) 存入数组后再自身 整除(/) 循环当自身被整除为0时退出。
下面的算法都与高精度乘法相同就不多赘述了。
PS: 上述代码最多可算到5w的阶乘哦(最好不要轻易尝试它的极限，因为数字越大，算的越慢)。