在平常写代码时对于加减乘除我们都是默认计算机可以一步到位,但计算机能够计算的范围很有限,这时我们就需要用到高精度算法。
什么是高精度算法?
高精度算法就是将特别大的天文数字用字符串的形式存储,再将其逐位计算。
高精度加法
高精度加法的核心思想就是模拟列竖式。
举例:17+8
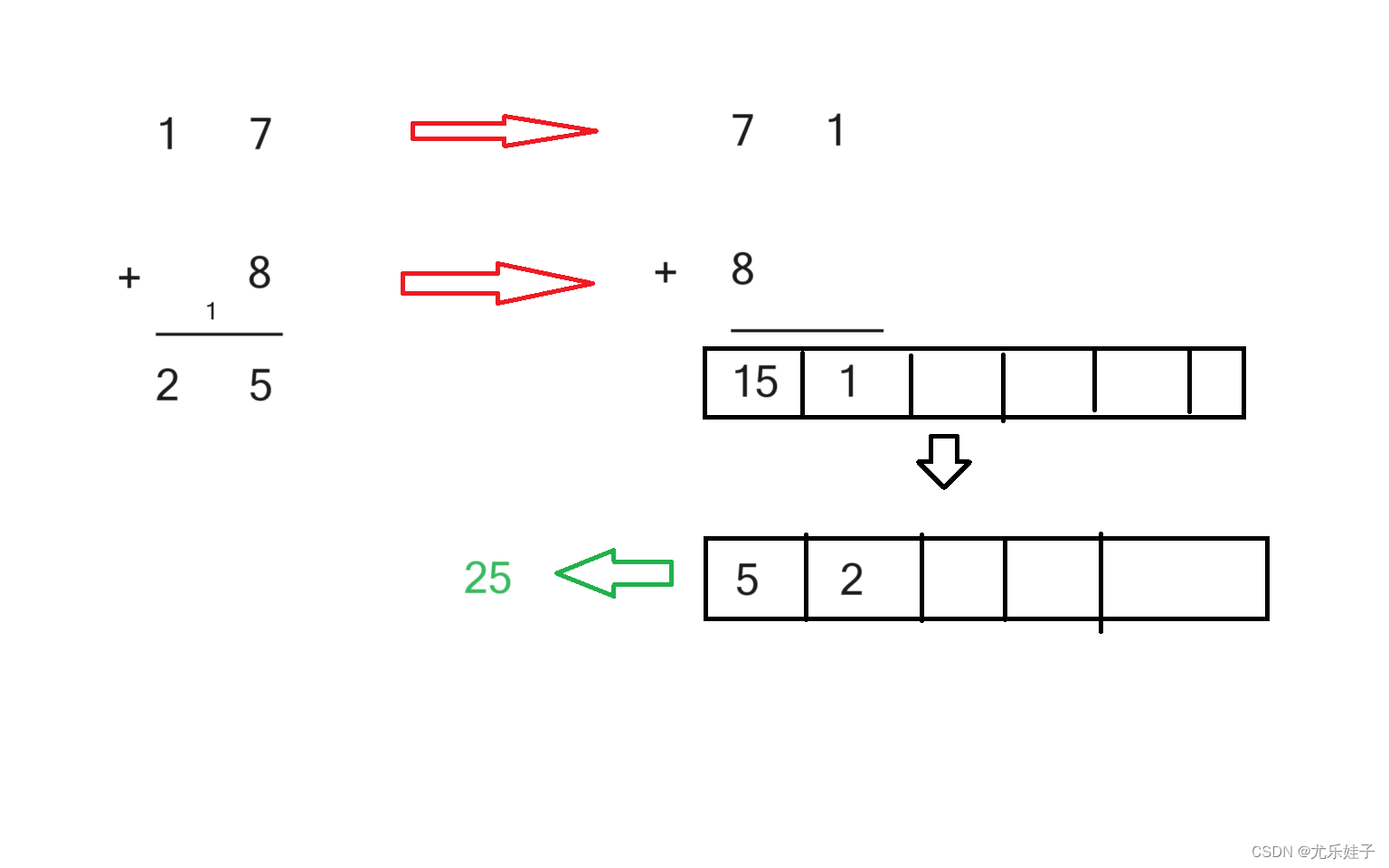
如果按照常规思想将数字转换成字符串再存入数组的话,个位上的8将会对齐到十位上的1,这就变成了17+80。为了确保能将数字字符逐位对齐存入数组,我们需将字符串先反转存入数组再相加,最后将超过10的数位进位。
代码如下:
#include<iostream>
#include<string.h>
using namespace std;
#define H 10086
char add[H], print[H];
int sum[H];
int main()
{
int len1, len2, maxlen, k = 0;
cout << "第一个加数:";
cin >> add;
len1 = strlen(add);
for (int i = len1 - 1; i >= 0; i--)sum[k++] += (add[i] - '0');
k = 0;
cout << "第二个加数:";
cin >> add;
len2 = strlen(add);
for (int i = len2 - 1; i >= 0; i--)sum[k++] += (add[i] - '0');
k = 0;
if (len1 > len2)maxlen = len1;
else maxlen = len2;
//进位
for (int i = 0; i < maxlen; i++)
{
if (sum[i] >= 10)
{
sum[i + 1]++;
sum[i] %= 10;
}
}
//反转并打印字符串
if (!sum[maxlen])maxlen--;
for (int i = maxlen; i >= 0; i--) print[k++] = sum[i] + '0';
cout << "和为:" << print;
}
- char
add[H]:将两个加数分别以字符形式写入字符串。print[H]:将作为最后输出的数组(也是字符串形式)。intsum[H]:作为用来计算每一位的数字和,并进位。 - int
len1:计算第一个加数的字符串长度。len2:计算第二个加数的字符串长度。maxlen:len1与len2中较长的长度。K:作为0号下标。 for (int i = len1 - 1; i >= 0; i--)sum[k++] += (add[i] - '0');将字符串反转写入数组。if (!sum[maxlen])maxlen--;查看答案具体有几位数。两个加数之和的位数最大为较大数位数+1,最小为较大数位数(比如2个两位数相加的和最大为3位数,最小为2位数)只有这两种可能。我们通过maxlen找到的较大数位数本身就是较大数位数+1(因为数组是从0号开始计算的)。再判断较大位数+1如果为0的话位数减一。for (int i = maxlen; i >= 0; i--) print[k++] = sum[i] + '0';将数组sum[]反向写入字符数组print[]。
高精度减法
高精度减法的核心思想依旧是模拟列竖式。
举例:17-23

举了一个比较特殊的例子,减出来是个负数,为了统一计算步骤我们交换两个减数的位置,并在最后输出结果前添加负号。与先前高精度加法类似,先将字符串反转存入数组再做差,最后将每位为负数的数位退位。
代码如下:
#include<iostream>
#include<string.h>
using namespace std;
#define H 10086
char num1[H], num2[H], print[H];//默认num1>num2;
int ans[H];
int main()
{
int len1, len2, maxlen, k = 0, flag = 0;
cout << "第一个减数:";
cin >> num1;
len1 = strlen(num1);
cout << "第二个减数:";
cin >> num2;
len2 = strlen(num2);
if (len1 > len2)maxlen = len1;
else maxlen = len2;
//若num1<num2,交换num1与num2
if (len2 > len1 || len1 == len2 && (strcmp(num1, num2) < 0))
{
flag = 1;
swap(len1, len2);
for (int i = 0; i < maxlen; i++)swap(num1[i], num2[i]);
}
//反转字符串写入数组
for (int i = len1 - 1; i >= 0; i--)ans[k++] += (num1[i] - '0');
k = 0;
for (int i = len2 - 1; i >= 0; i--)ans[k++] -= (num2[i] - '0');
k = 0;
//退位
for (int i = 0; i < maxlen; i++)
{
if (ans[i] < 0)
{
ans[i + 1]--;
ans[i] += 10;
}
}
//反转写入字符串并打印
while (!ans[maxlen] && maxlen > 0)maxlen--;
for (int i = maxlen; i >= 0; i--) print[k++] = ans[i] + '0';
cout << "差为:";
if (flag)cout << "-";
cout << print;
}
- char
num1[H]:作为被减数。num2[H]:作为减数。(默认被减数>减数)。print[H]:将作为最后输出的数组。intans[H]:作为用来计算每一位的数字差,并退位。 - int
flag:作为判断是否为负数。 - 交换被减数与减数位置:
//若num1<num2,交换num1与num2
if (len2 > len1 || len1 == len2 && (strcmp(num1, num2) < 0))
{
flag = 1;
swap(len1, len2);
for (int i = 0; i < maxlen; i++)swap(num1[i], num2[i]);
}
先判断len2与len1的关系,若len2>len1说明减数大于被减数。再判断当len1=len2时字符串num1[]和num2[]每一位的关系(在这用strcmp())。
交换步骤:
- 激活
flag。在最后打印结果前打印负号。 - 交换
len1和len2的值。因为交换了数组num1[]与num2[]所以长度也要变。 - 循环依次交换
num1[]与num2[]的值(循环次数选两字符串中较大的)。
- 反转写入字符串并打印:
与高精度加法稍有不同的地方:
while (!ans[maxlen] && maxlen > 0)maxlen--;判断数组最后一位是否为0,往前循环直到数组非0时结束循环并记录非0的起始位置。而maxlen > 0是为了避免两数之差刚好为0时ans[]数组内所有元素都为0使得下标脱离ans[]数组范围,导致打印出空字符。
if (flag)cout << "-";当flag从0变为1后在打印print[]字符串前先打印负号。
高精度乘法
还是模拟列竖式。
举例:15x16

从图解可以看出高精度乘法相比高精度加法和高精度减法稍微复杂一点,需要两个循环嵌套(循环次数最大为len1xlen2)。
代码如下:
#include<iostream>
#include<string.h>
using namespace std;
#define H 10086
char num1[H], num2[H], print[H];
int ans[H];
int main()
{
int len1, len2, maxlen, k = 0;
cout << "请输入第一个因数;";
cin >> num1;
len1 = strlen(num1);
cout << "请输入第二个因数:";
cin >> num2;
len2 = strlen(num2);
maxlen = len1 + len2;
//反转字符串
for (int i = len1 - 1; i >= len1 / 2; i--)swap(num1[k++], num1[i]);
k = 0;
for (int i = len2 - 1; i >= len2 / 2; i--)swap(num2[k++], num2[i]);
k = 0;
//模拟乘法竖式
for (int i = 0; i < len1; i++)
{
for (int j = 0; j < len2; j++)
{
ans[i + j] += (num1[i] - '0') * (num2[j] - '0');
}
}
//进位
for (int i = 0; i < maxlen; i++)
{
if (ans[i] >= 10)
{
ans[i + 1] += ans[i] / 10;
ans[i] %= 10;
}
}
//反转写入字符串并打印
while (!ans[maxlen] && maxlen > 0)maxlen--;
for (int i = maxlen; i >= 0; i--) print[k++] = ans[i] + '0';
cout <<"积为:" << print;
}
maxlen = len1 + len2;与高精度加法/高精度减法不同,此时maxlen并不是取len1和len2最大值,而是取二者之和。因为在乘法中积的位数只能确定最大不超过两个因数的位数和,所以先取最大位数,多了再减。- 模拟乘法竖式:
//模拟乘法竖式
for (int i = 0; i < len1; i++)
{
for (int j = 0; j < len2; j++)
{
ans[i + j] += (num1[i] - '0') * (num2[j] - '0');
}
}
两个循环完美模拟了两个因数的乘积(外层循环模拟第一层因数,内存循环模拟第二层因数)。其中ans[i+j]也完美复刻了积所存放的位置。
- 反转写入字符串并打印与高精度减法几乎别无二致。
高精度除法
高精度除法与高精度加/减/乘不一样,并不需要列竖式模拟而且高精度除法还分为高精度÷低精度(高精度用字符串表示,低精度用long long开变量)和高精度÷高精度两类。
高精度除低精度:
举例1234÷56

相比高精度加/减/乘的列竖式模拟思想,高精度除法思想更简单,这里图片不直观我们直接上代码。
代码如下:
#include<iostream>
#include<string.h>
using namespace std;
#define H 10086
char num1[H], print[H];
int ans[H];
int main()
{
long long len1, num2, number = 0;
cout << "请输入被除数:";
cin >> num1;
len1 = strlen(num1);
cout << "请输入除数;";
cin >> num2;
for (int i = 0; i < len1; i++)
{
number *= 10;
number += num1[i] - '0';
ans[i] = number / num2;
number %= num2;
}
//写入字符串并打印
int k = 0, c = 0;
while (!ans[k] && k < len1 - 1)k++;
for (int i = k; i < len1; i++) print[c++] = ans[i] + '0';
cout << "商为:" << print;
}
- 由于是高精度÷低精度所以只需要定义一个
num1[H]和一个计算字符串长度的len1就行。long long定义一个num2存储低精度数据,number作为每次计算的余数(作为下一位的被除数)。 - 核心代码:
for (int i = 0; i < len1; i++)
{
number *= 10;
number += num1[i] - '0';
ans[i] = number / num2;
number %= num2;
}
number *= 10;每次将被除完剩下的余数×10作为下一位的被除数(从第二次循环开始)。number += num1[i] - '0';加上本位该被除的数。
以上两句合并起来组成了每一位该被低精度数除的被除数。ans[i] = number / num2;将被除数÷低精度数的值赋给本位数组。number %= num2;将number的值变为被低精度数除完后的余数。- 写入字符串并打印:
intk=0:因为高精度÷低精度并没有列竖式模拟,自然也没有反转字符串,所以定义k是从0开始作为起始下标。c=0:作为起始下标。 while (!ans[k] && k < len1 - 1)k++;因为计算是按顺序执行,需要将前几位的0全部去掉,而k<len1-1是防止最后答案全是0而导致全部去掉从而下标超出ans[]范围,所以要确保留下最后一位。























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








