二分答案法及例题-CSDN博客

本文链接：https://blog.csdn.net/2301_80186482/article/details/143170444

文章目录

一、什么是二分答案
二、例题
三、二分答案法分析步骤
四、总结

一、什么是二分答案

二分答案是一种对答案去进行二分搜索的方法，它是一种解题技巧，一般使用到二分答案的题目，常常是让在某个条件确定的情况下，让你求最大或者最小的答案来满足这个条件，且它的答案具有单调性，而且这种题目通常正向去求是很难的，而反向去求比较简单，多说无益，我们通过题目去理解他到底是怎么去应用的。

二、例题

1. 伐木工

在这里插入图片描述
测试链接

题目解读：

它的要求是给我们n棵树的高度，让我们找到一个砍树的高度H，每棵树比H高的部分会被砍下来作为我们得到的木材长度，问怎么样去确定这个高度H，使H在最大的情况下我们还能获得总和为M米的木材。

题目分析：

我们正常去想怎么确定H呢，这个就比较麻烦了，它既要让H尽可能大，还要满足最后总和为M，我们可以反过来想，如果我们提前知道了H，再去判断它的木材总和是否满足等于M，是不是就很容易了，通过循环整个数组去和H相减，累加它的余值，即可得到它的木材总长。
那么我们再来看看H又有什么特点，我们可以发现，H的取值范围是从0~max（最高的高度），H一定是在这个范围内，当我们的H到达最高的树的高度时候，其实已经没有意义了，就算我们在增大高度，这时候它得到的木材都是0，而H最小也只能是0，我们最多就是把所有的树全部砍掉去得到木材，如此来看，H的范围是一个连续的，符合二分区间单调的条件。
接下来我们可以分析分析，H和M之间又有什么关系呢，当我们H越大的时候，得到的木材其实越少，即M越小，H越小，得到的木材越多，即M越大，这样是不是类似于我们二分当中的当一个数不满足条件，我们就去左边或者右边去再次搜索，而这里的木材总长M即为我们的条件，H即为这个数，这样来看，二分是不是就很明显了。

我们来看一下代码：

#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+10;
int n,m,ma,ans;
int a[N];
bool check(int h) {
	long long sum = 0;
	for (int i = 1; i <= n; i++) {
		if(a[i] > h)
		sum += a[i] - h;
	}
	if (sum >= m) return 1;
	else return 0;
}
int main() {
	cin>>n>>m;
	for (int i = 1; i <= n; i++) {
		cin>>a[i];
		ma = max(a[i],ma);
	}
	sort(a+1,a+n+1);
	int l = 0, r = ma, mid = 0;
	while (l <= r) {
		mid = l + (r-l)/2;
		if (check(mid)) {
			l = mid + 1;
			ans = mid;
		}
		else r = mid - 1;
	}
	cout<<ans;
	return 0;
}

2. 跳石头

在这里插入图片描述

测试链接

题目解读：

这道题主要说的是，有一段路上放了N块石头，现在我们要移走M石头，使得每个石头之间的距离尽可能的大。

题目分析：

首先我们还是正向思考，怎么去确定这个距离呢，移走M块，移走哪些就是一个问题，而且要求每个石头距离尽可能大，有些小伙伴就会问那我去循环，找所有可能的情况去算，如果没有时间限制，这或许可以求出答案，但是要去枚举所有情况，这个时间复杂度是很高的，所以我们还是去反向思考，当距离固定的时候，我们遍历数组元素，求出需要移走多少石头，看能否满足M即可。
我们先来分析这个距离的答案范围，不难想到，为0~L，他最大就是从起点跳到终点，所以最大为L（我们发现，其实我们最主要确定的就是最大值是多少，最小值一般是0，因为即便不会有0这种答案，此时0肯定是不满足条件的，不满足条件，它也得不到这个值，但也要注意有些特殊题目）我们在看M和距离d的关系，d越大，则移走的石块越多，即M越大，d越小，则移走的石块越少，即M越小。符合二分的特点，满足条件往一边走，不满足条件往另一边走。

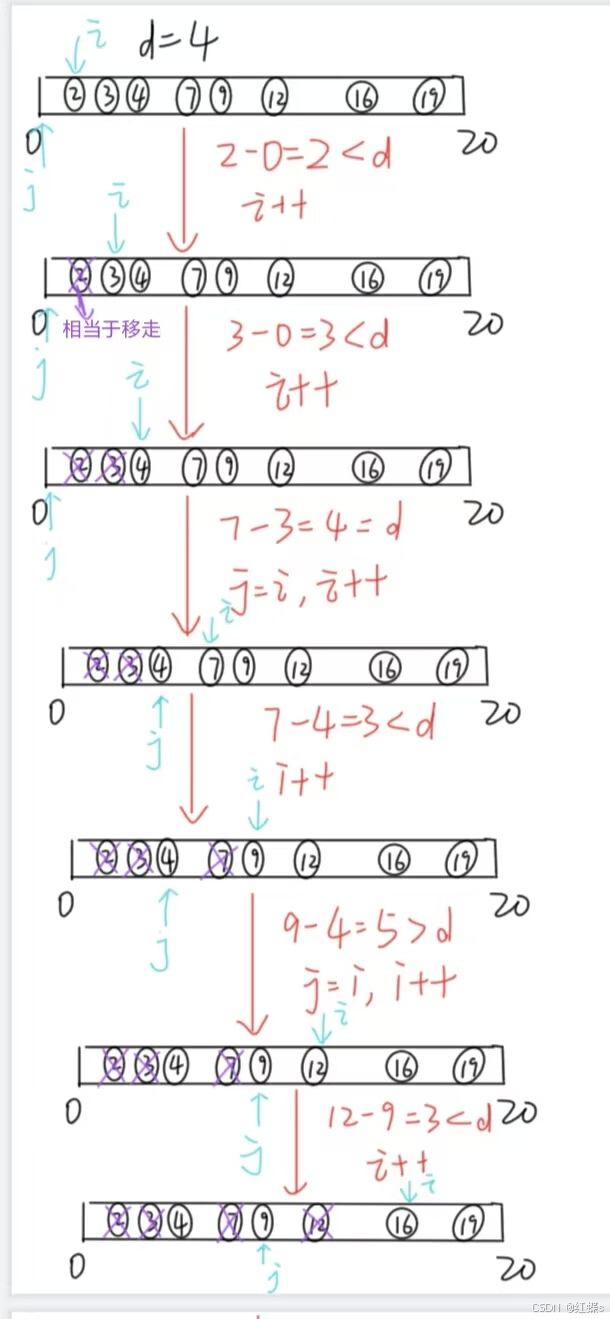
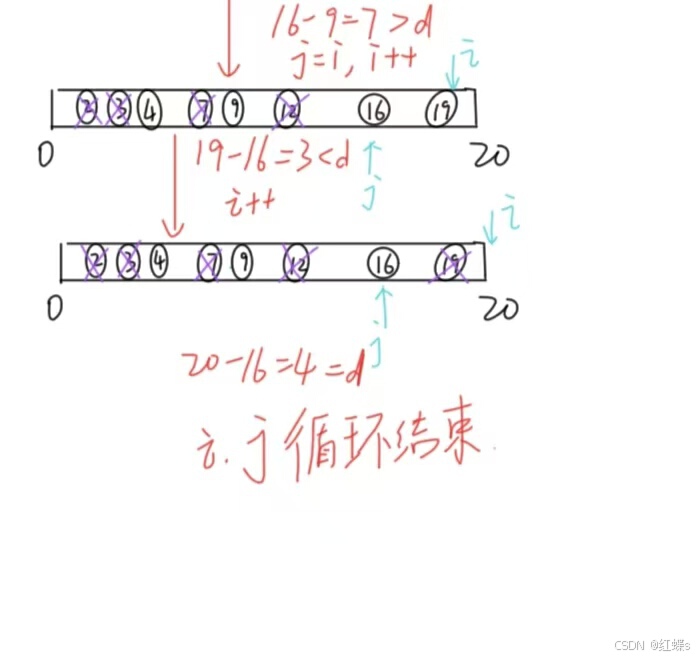
这道题的check用到了一个小技巧，大家结合代码理解一下，类似于双指针，它的思想就是一个指针i一直往前遍历，另一个指针j不动，当我们i和j两个石块间距离<d(最小距离)的时候，sum++(即这个石块距离不符合条件，我们移走了，移走石块数加一)，i继续向后遍历，j不变，当满足>d的时候，表示我们找到了下一个石块，让j跳到i的位置，i继续向后遍历。
我给大家画了一下图，比较简陋，大家可以看看

代码如下

#include <bits/stdc++.h>
using namespace std;

const int N = 5e5+10;
int a[N];
int len,n,m,ans;
bool check(int d) {
    int sum = 0;
    for (int i = 1,j = 0; i <= n+1;) {
        if (a[i] - a[j] < d) {
            i++;
            sum++;
        }
        else j = i,i++;
    }
    if (sum <= m) return 1;
    else return 0;
    
}
int main() {
	cin>>len>>n>>m;
	for (int i = 1; i <= n; i++) cin>>a[i];
	a[n+1] = len;
	int l = 0, r = len, mid = 0;
	while (l <= r) {
	    mid = (r + l) / 2;
	    if(check(mid)) {
	        l = mid + 1;
	        ans = mid;
	    }
	    else r = mid - 1;
	}
	cout<<ans;
	return 0;

}