希尔排序

文章目录

• 前言
• 一.直接插入排序(时间复杂度N^2)
• 二.希尔排序
• 时间复杂度

---

前言

今天我们来讲一下排序算法中的插入排序中的希尔排序,插入排序分为两种，一种是直接插入排序，另一种就是希尔排序

---

一.直接插入排序(时间复杂度N^2)

我们这个排序，我们就以默认的排升序为主，就是说给你一组随机的数，我要把它排成顺序有很多种算法，这些排序在应对不同的数据中有好坏，所以我们才需要学习这些排序方法。

然后我们来看直接插入算法，这个方法跟名字来看就是直接插入

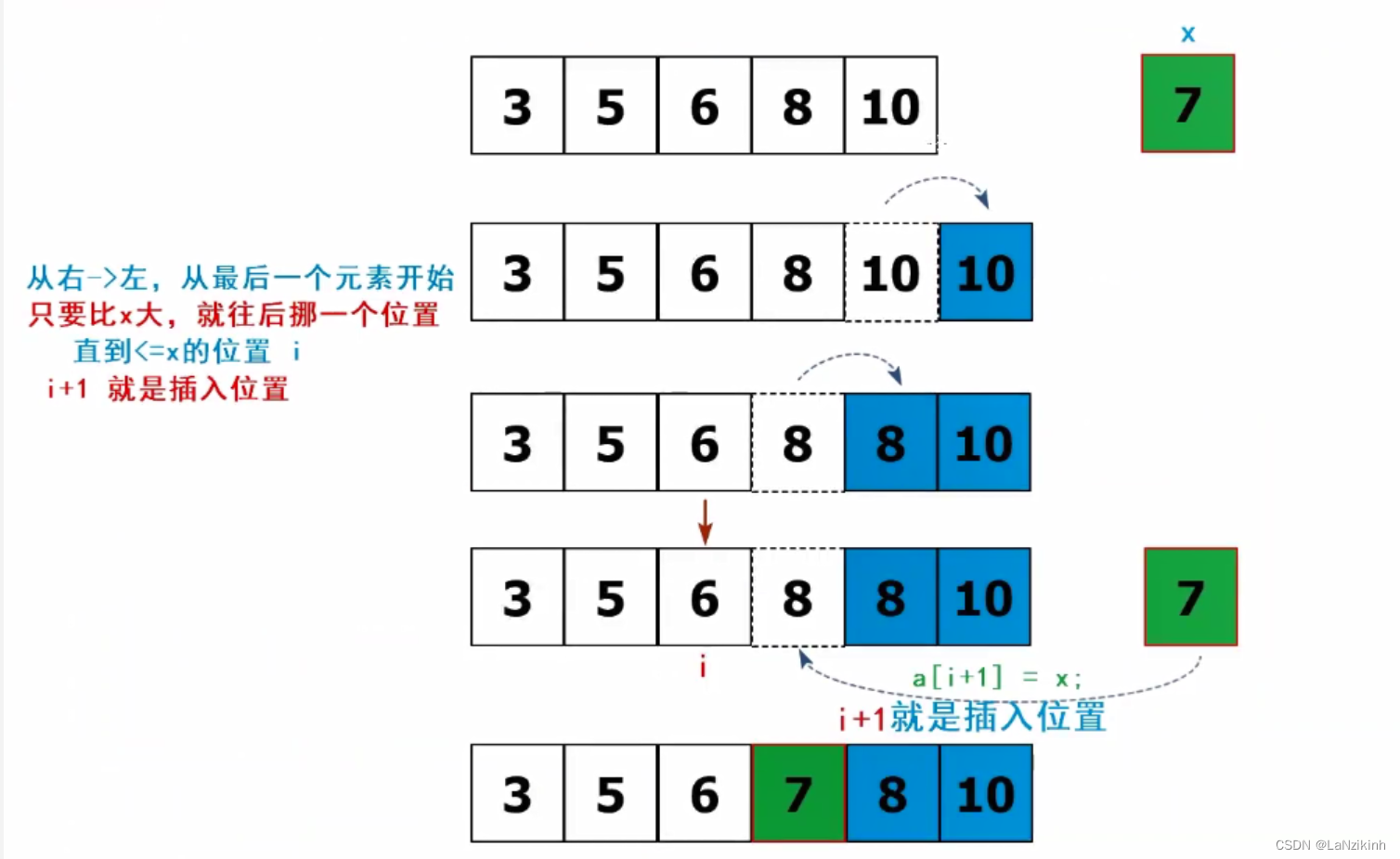
思路：当插入第i（i>=1)个元素的时候，前面的arr[0],.....arr[i-1],已经排好序，此时拥有arr[i]的排序码与arr[i-1]比较，看是插在他前面还是插在他后面就可以了。

void InsertSort(int* a, int n)
{
	//[0,end]有序，end+1位置的值插入[0,end]中，让[0,end+1]也有序
	for (int i = 0; i < n - 1; i++)
	{
		int end = i;
	//把当前end+1的值贮存下来，用来比较
		int tmp = a[end + 1];
		//为什么要end>=0,因为数据除了和不仅要和前面的数比，还要和前面所有的数去比
		while (end >= 0)
		{
			//如果大，就往后挪
			if (a[end] > tmp)
			{
				//为什么只有end+1换了，因为我之前保存了tmp的值，所以后续只用tmp去比较就可以了
				a[end+1] = a[end];
				end--;
			}
			//如果小，大的就在后面待着
			else
			{
				break;
			}
		}
	    //因为大的就在后面待着，所以在我出循环之后，将这个数据放在当前end之后
		a[end + 1] = tmp;
	}

二.希尔排序

概念

希尔排序(Shell Sort)是插入排序的一种，它是针对直接插入排序算法的改进。

希尔排序又称缩小增量排序，因 DL.Shell 于 1959 年提出而得名。

它通过比较相距一定间隔的元素来进行，各趟比较所用的距离随着算法的进行而减小，直到只比较相邻元素的最后一趟排序为止。

希尔排序，他又称为缩小量排序，其实他就是直接插入排序的一种优化，他的主要思路就是预排序

思路:多组间隔为gap的预排序，由大变小，gap越大，大的数可以越快的到后面，小的数可以越快的到前面，gap越大与排序越不接近有序，gap越小越接近有序，当gap==1的时候就是直接插入排序

void shellsort(int* a, int n)
{
	int gap = n;
	while(gap>1)
	{
		gap = gap / 2;
		//把间隔为gap的同时排
		//为什么是i < n - gap，因为超过这个就越界了
		for (int i = 0; i < n - gap; i++)
		{
			//这个里面是一次间隔为gap的排序
			int end = i;
			int tmp = a[end + gap];
			while (end >= 0)
			{if (a[end] > tmp)
				{
					a[end + gap] = a[end];
					end-=gap;
				}
				else
				{
					break;
				}
			}
			a[end + gap] = tmp;
		}
	}
}

如果实在无法理解希尔排序，可以直接写一个插入排序，把1换成gap就可以了

时间复杂度

希尔排序的时间复杂度是O(N*log2 N)

时间复杂度是最坏的结果,直接插入排序最坏的结果就是全是混乱的，每一个都要从头排到位，所以就是N的平方,而希尔排序我通过间隔gap即使我每一次都要从头排到尾，但是我排的次数是一半一半的递减的，所以是log2 N次,时间复杂度是O(N*log2 N)