数据结构与算法（3）-双向链表与栈与队列

于 2025-10-08 17:20:03 发布
阅读量704 收藏 16
点赞数 36
CC 4.0 BY-SA版权
分类专栏： 数据结构与算法 文章标签： 数据结构 双向链表 栈 队列
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/2301_80484013/article/details/152728508

1.书接上文

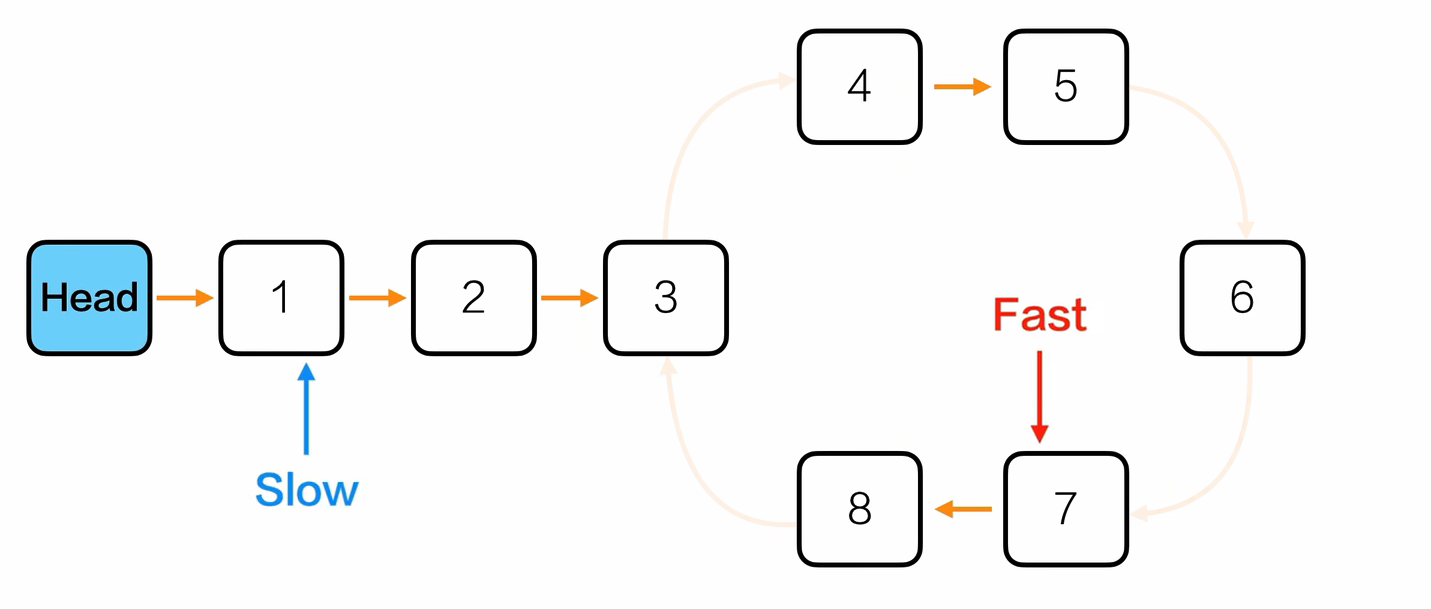
如何找到环的入口?

  1. 先确定环有几个节点,fast和slow相遇的那个节点,设置一个p指向此节点,count来计数

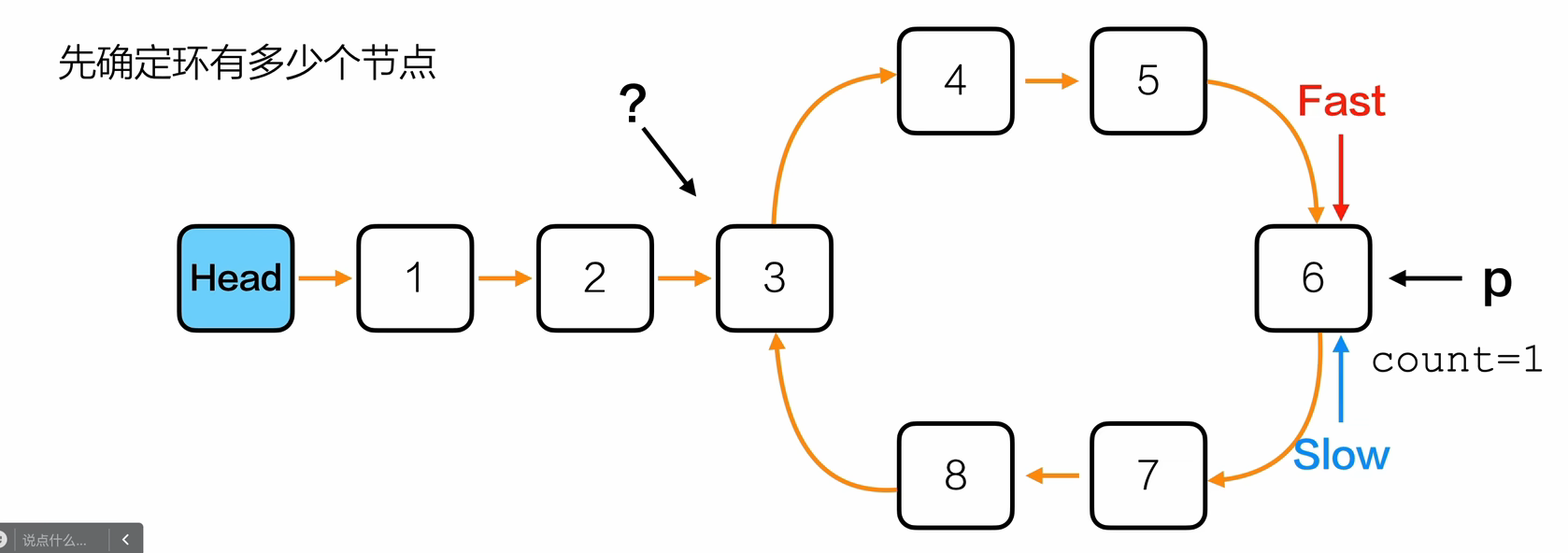
  1. 让p走,直到p再次遇到fast或者让fast走直到fast再次等于p

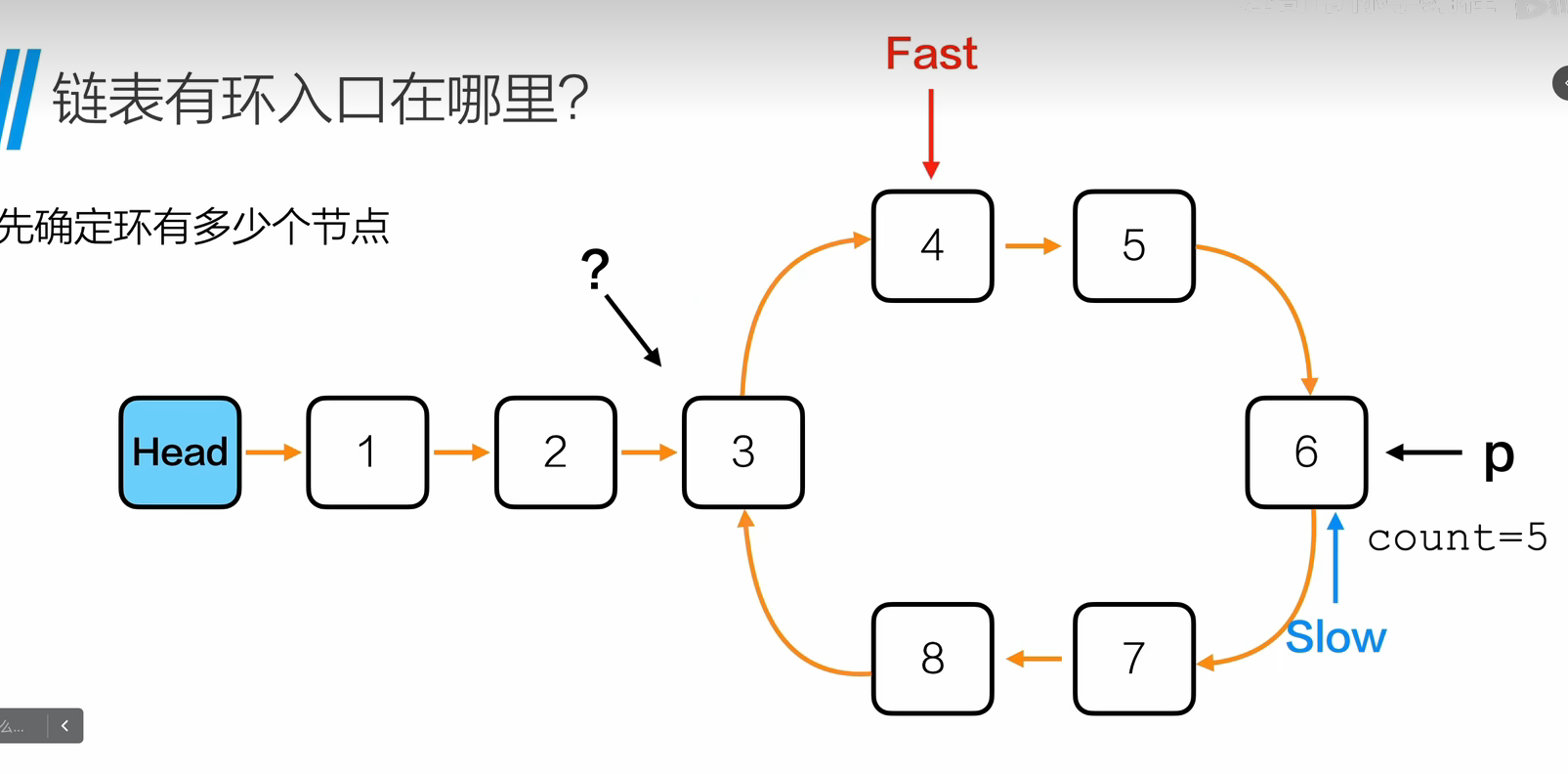
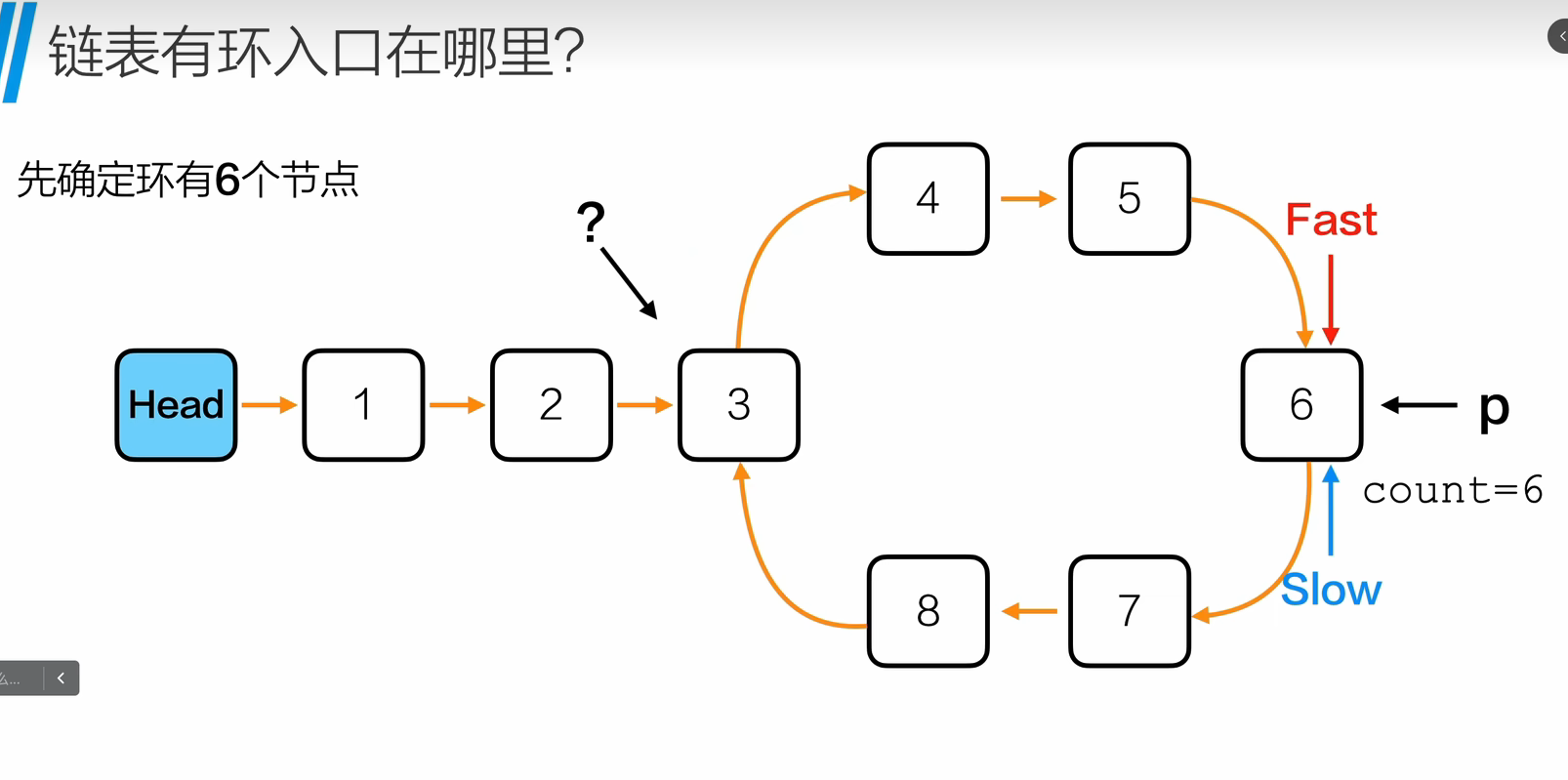
此时count=6,意味着环有六个节点

说明第一次循环fast指针比slow指针多走六步

  1. 重新让fast和slow指针指向头节点,fast比slow先走6步,然后同步走.下次相遇的时候指向的就是环的入口

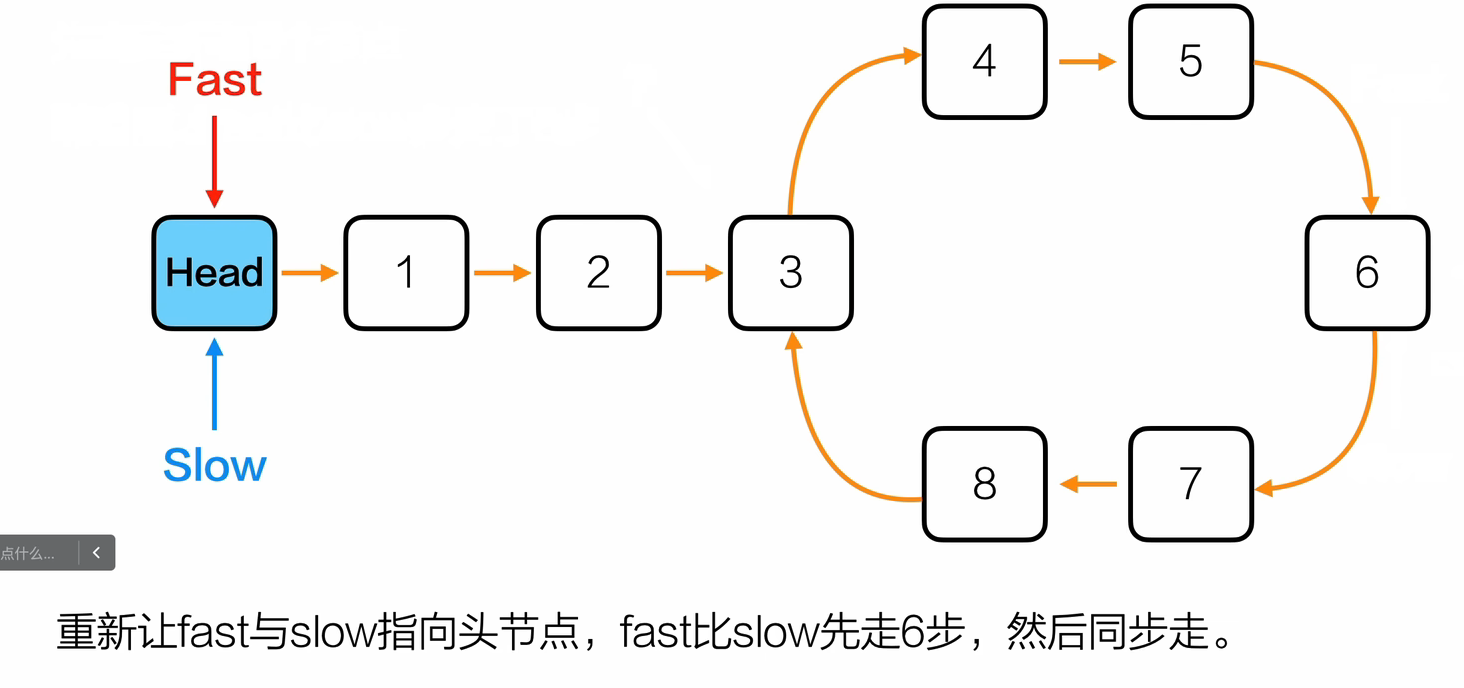
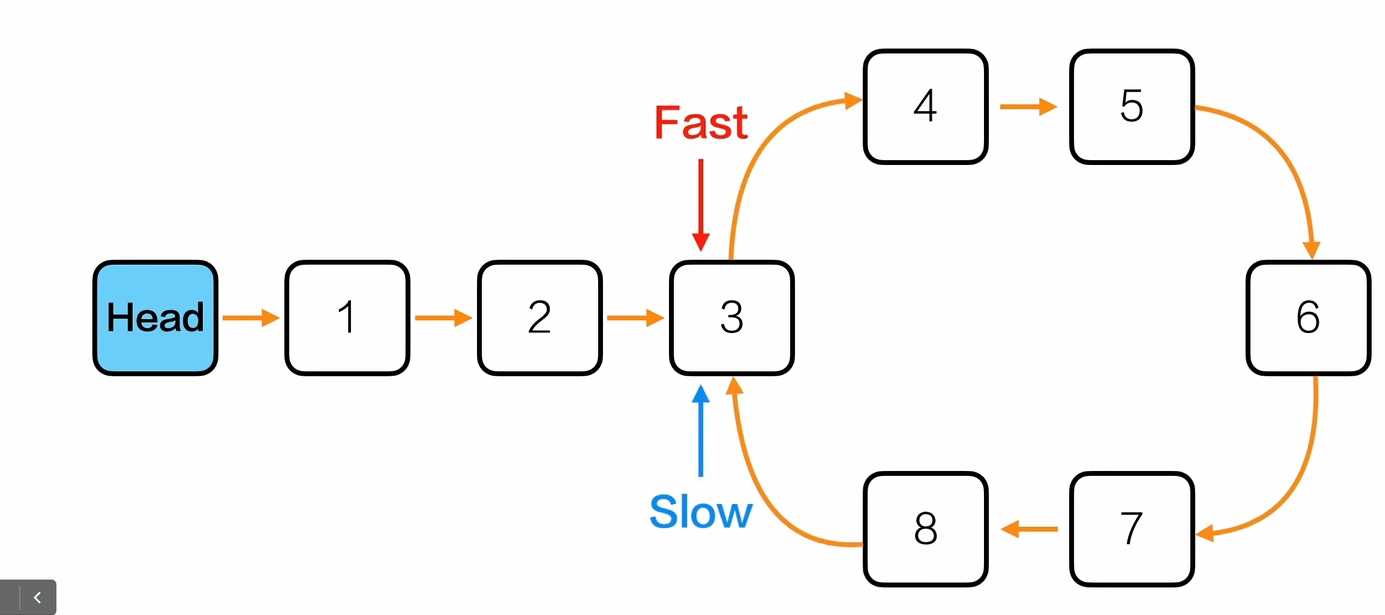
// 找到链表环的入口节点
Node* findBegin(Node *head)
{
    Node *fast = head;
    Node *slow = head;

    // 第一步：判断是否有环
    while (fast != NULL && fast->next != NULL)
    {
        fast = fast->next->next;
        slow = slow->next;

        // 如果快慢指针相遇，说明有环
        if (fast == slow)
        {
            // 第二步：计算环的长度
            Node *p = fast;
            int count = 1;
            while (p->next != slow)
            {
                count++;
                p = p->next;
            }

            // 第三步：找环的入口
            fast = head;
            slow = head;

            // 让 fast 先走 count 步
            for (int i = 0; i < count; i++)
            {
                fast = fast->next;
            }

            // fast 和 slow 同时前进，相遇处就是环的入口
            while (fast != slow)
            {
                fast = fast->next;
                slow = slow->next;
            }

            return slow;  // 返回环入口节点
        }
    }

    return NULL; // 无环返回空
}

完整例子:

#include <stdio.h>
#include <stdlib.h>

typedef int ElemType;

// 定义链表节点结构
typedef struct node {
    ElemType data;
    struct node *next;
} Node;

// 创建一个空链表（带头结点）
Node* initList() {
    Node *head = (Node*)malloc(sizeof(Node));
    head->next = NULL;
    return head;
}

// 尾插法建立链表
Node* insertTail(Node *head, ElemType e) {
    Node *p = (Node*)malloc(sizeof(Node));
    p->data = e;
    p->next = NULL;

    Node *tail = head;
    while (tail->next != NULL)
        tail = tail->next;

    tail->next = p;
    return head;
}

// 打印链表（最多打印20个，防止死循环）
void printList(Node *head) {
    Node *p = head->next;
    int count = 0;
    while (p != NULL && count < 20) {
        printf("%d -> ", p->data);
        p = p->next;
        count++;
    }
    printf("NULL\n");
}

// 查找环的入口
Node* findBegin(Node *head) {
    Node *fast = head;
    Node *slow = head;

    // 第一步：判断是否有环
    while (fast != NULL && fast->next != NULL) {
        fast = fast->next->next;
        slow = slow->next;

        if (fast == slow) {
            // 第二步：计算环的长度
            Node *p = fast;
            int count = 1;
            while (p->next != slow) {
                count++;
                p = p->next;
            }

            // 第三步：寻找环的入口
            fast = head;
            slow = head;
            for (int i = 0; i < count; i++) {
                fast = fast->next;
            }

            while (fast != slow) {
                fast = fast->next;
                slow = slow->next;
            }

            return slow; // 环入口
        }
    }

    return NULL; // 无环
}

int main() {
    // 创建链表
    Node *head = initList();
    for (int i = 1; i <= 6; i++) {
        insertTail(head, i);
    }

    // 手动制造一个环：让最后一个节点指向第3个节点
    Node *p = head->next;
    Node *third = NULL;
    Node *tail = NULL;

    int count = 1;
    while (p != NULL) {
        if (count == 3) third = p; // 记录第3个节点
        if (p->next == NULL) tail = p; // 记录最后一个节点
        p = p->next;
        count++;
    }
    if (tail && third)
        tail->next = third; // 形成环

    // 检测并找到环的入口
    Node *entry = findBegin(head);
    if (entry != NULL)
        printf("链表存在环，入口节点的值为：%d\n", entry->data);
    else
        printf("链表无环。\n");

    return 0;
}

2.双向链表

链式存储结构的节点中只有一个指示直接后继的指针域，由此，从某个结点出发只能顺指针向后寻查其他节点。若要寻查结点的直接前驱，则必须从表头指针出发。换句话说，在单链表中，查找直接后继的执行时间为 O(1)，而查找直接前驱的执行时间为 O(n)。
为克服单链表这种单向性的缺点，可利用双向链表（Double Linked List）。在双向链表的节点中有两个指针域，一个指向直接后继，另一个指向直接前驱

typedef int ElemType;
typedef struct node
{
    ElemType data;
    struct node *prev,*next;
}Node;

  1. 头插法

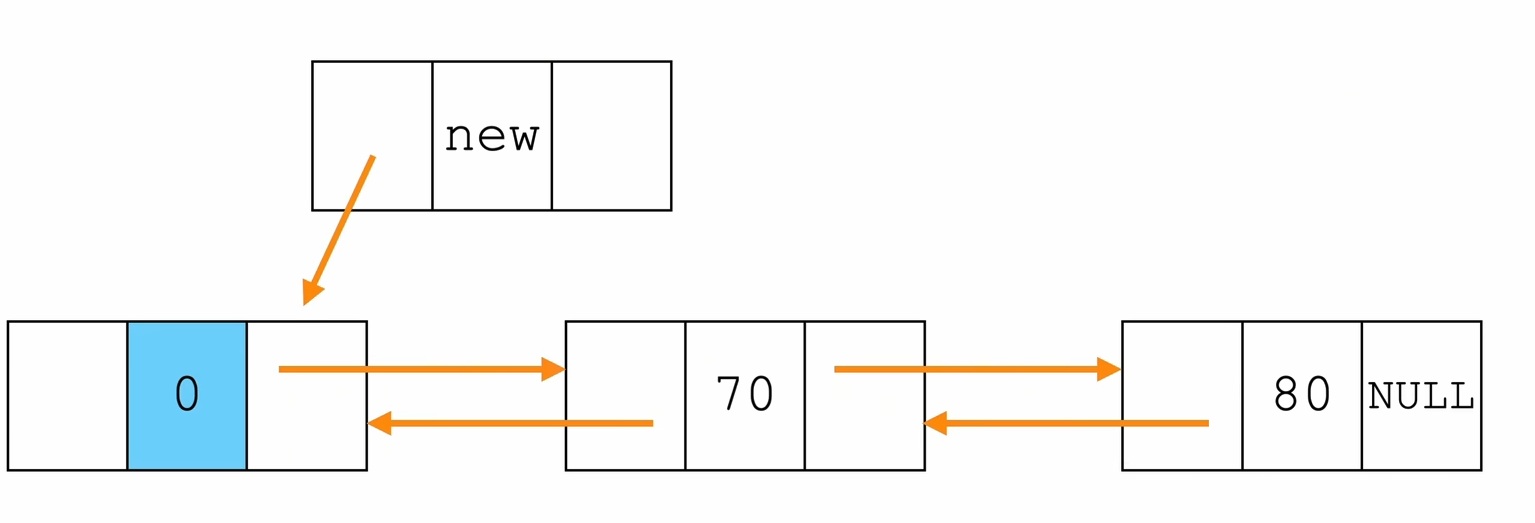
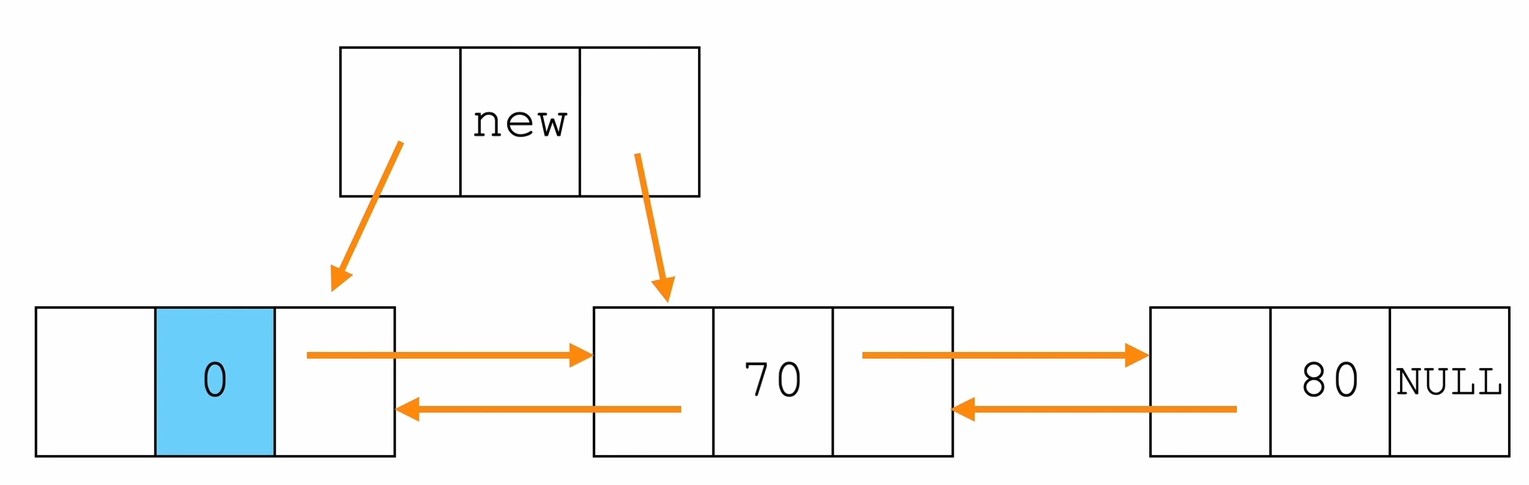
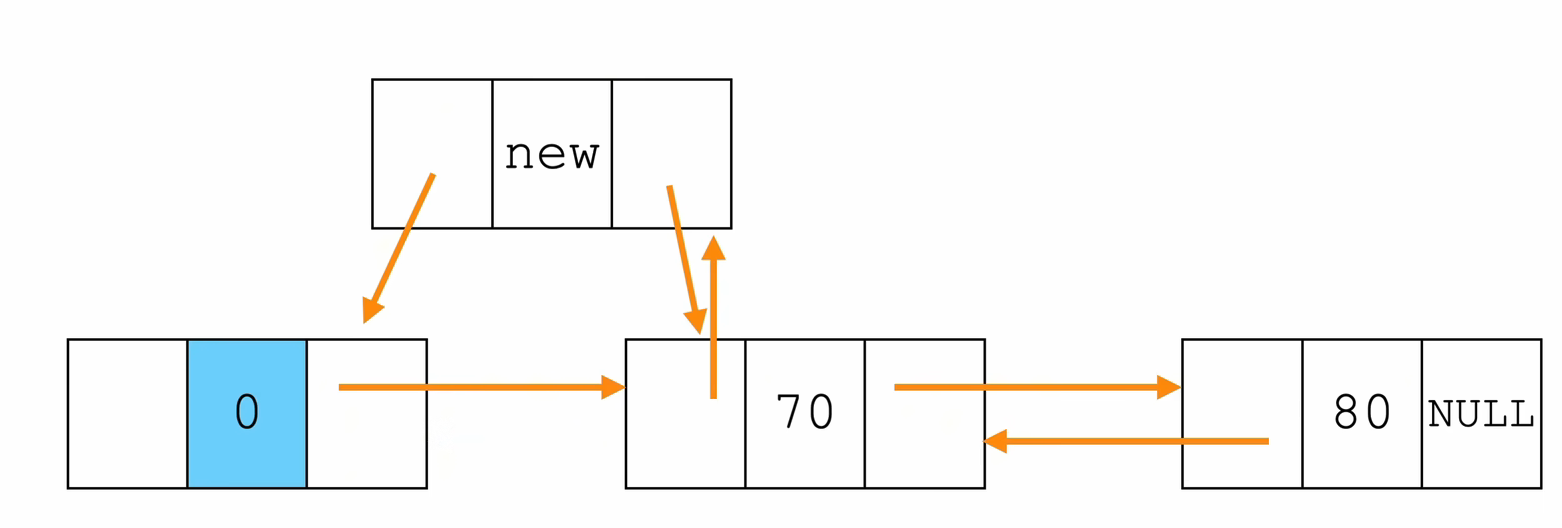
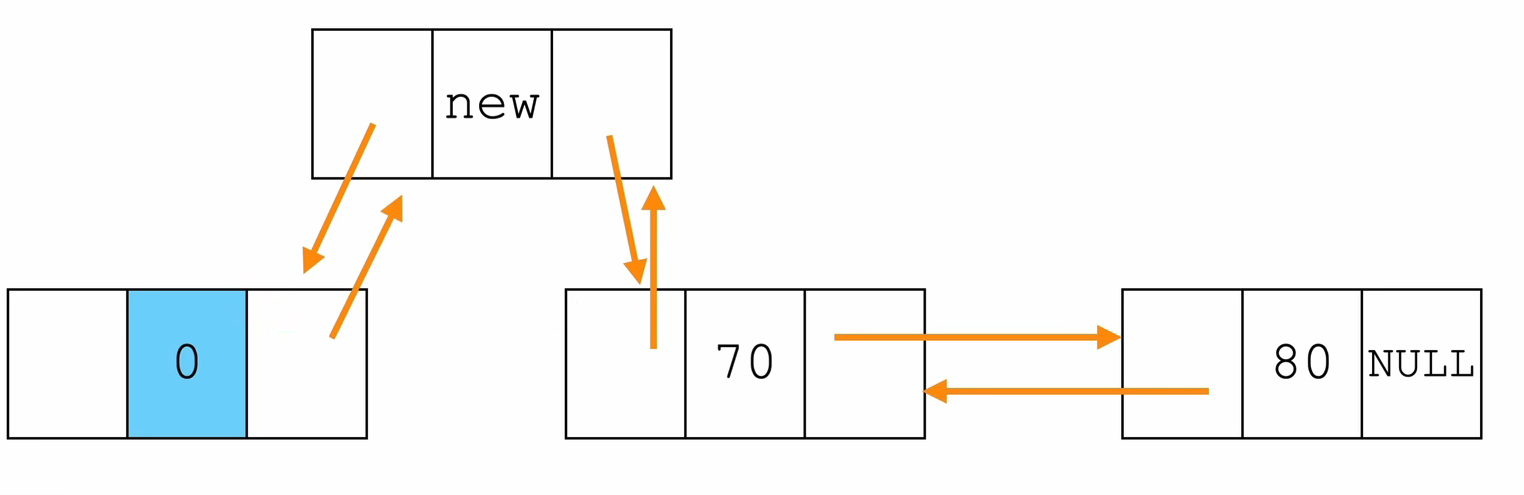
// 在 双向链表 的 头结点 L 之后，插入一个新节点 p
int insertHead(Node* L,ElemType e){
    Node *p=(Node*)malloc(sizeof(Node));
    p->data=e;
    p->prev=L;
    p->next=L->next;
// 如果原本链表不为空（也就是 头节点L之后确实还有节点），
// 那么原来第一个节点（即 L->next）的 prev 指针，
// 要从原来的 L 改成现在的 p
    if (L->next!=NULL)
    {
        L->next->prev=p;
    }
    L->next=p;
    return 1;
}
  1. 尾插法

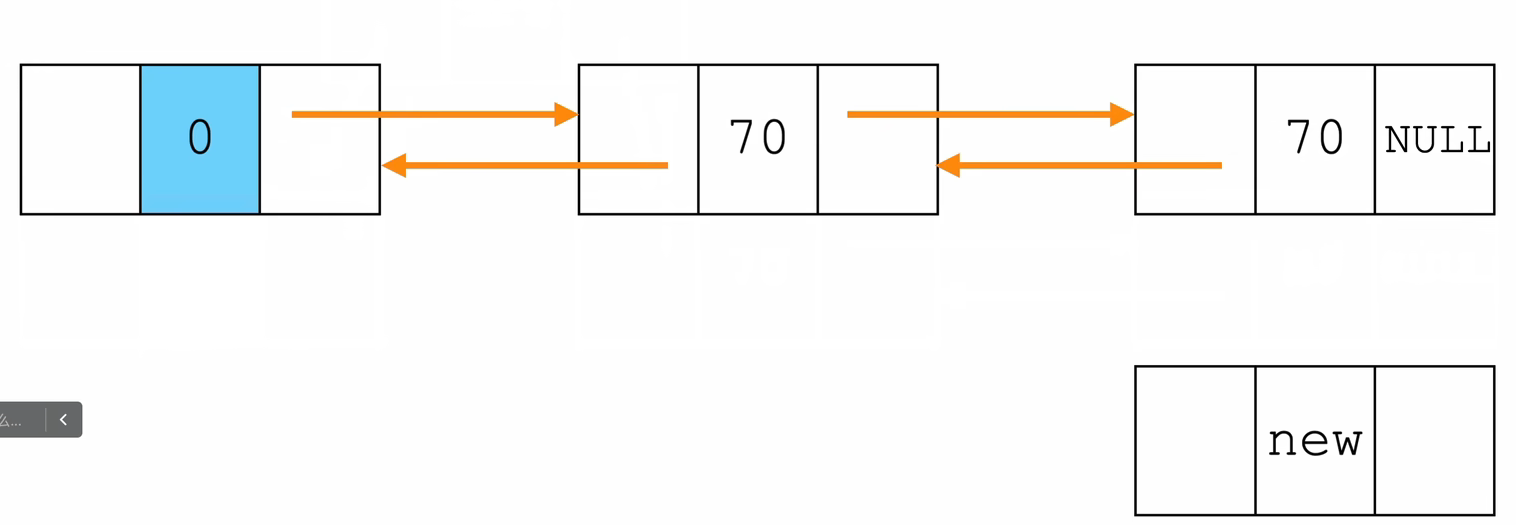
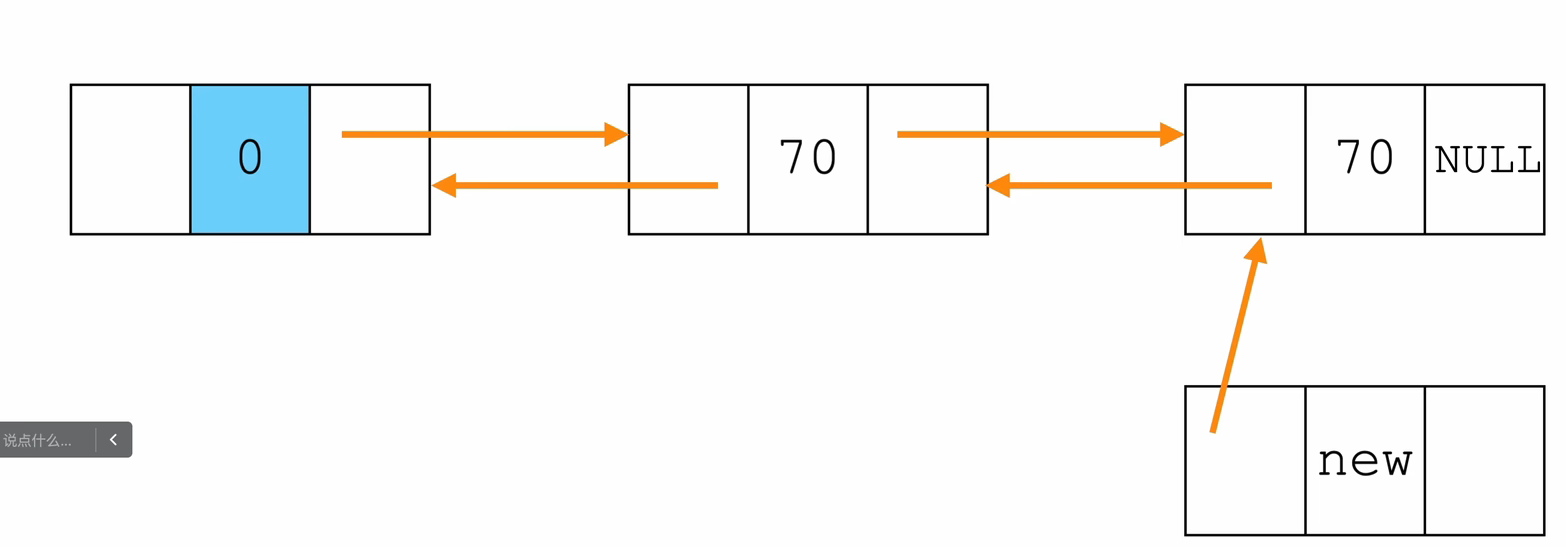
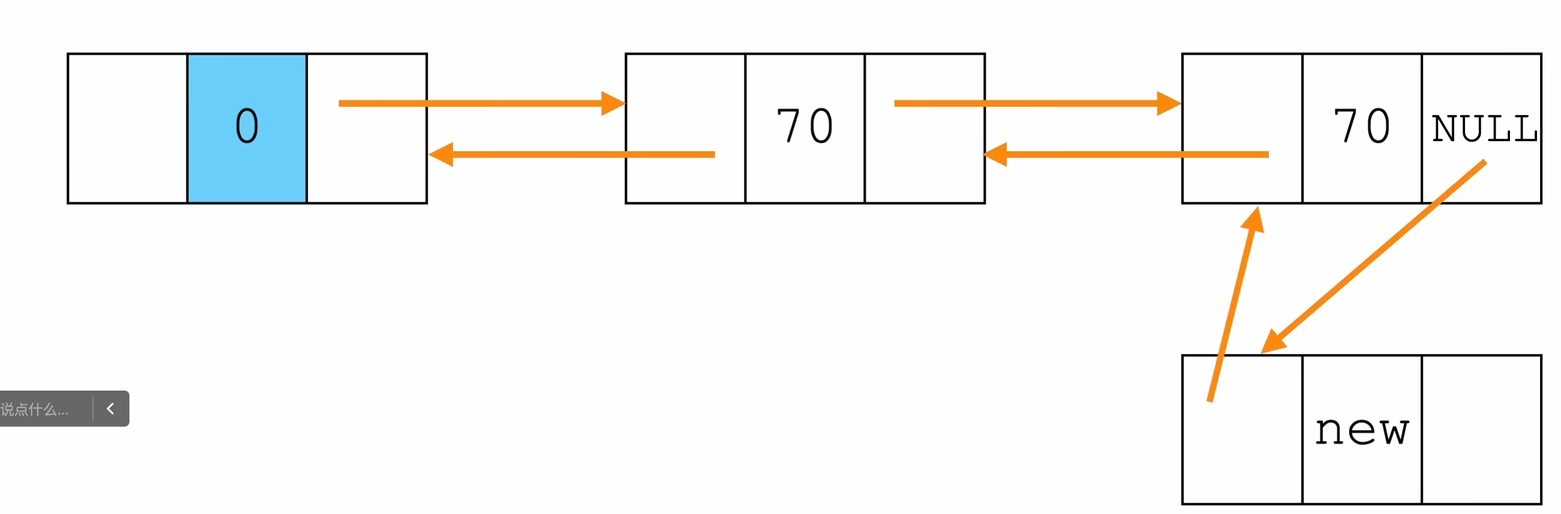
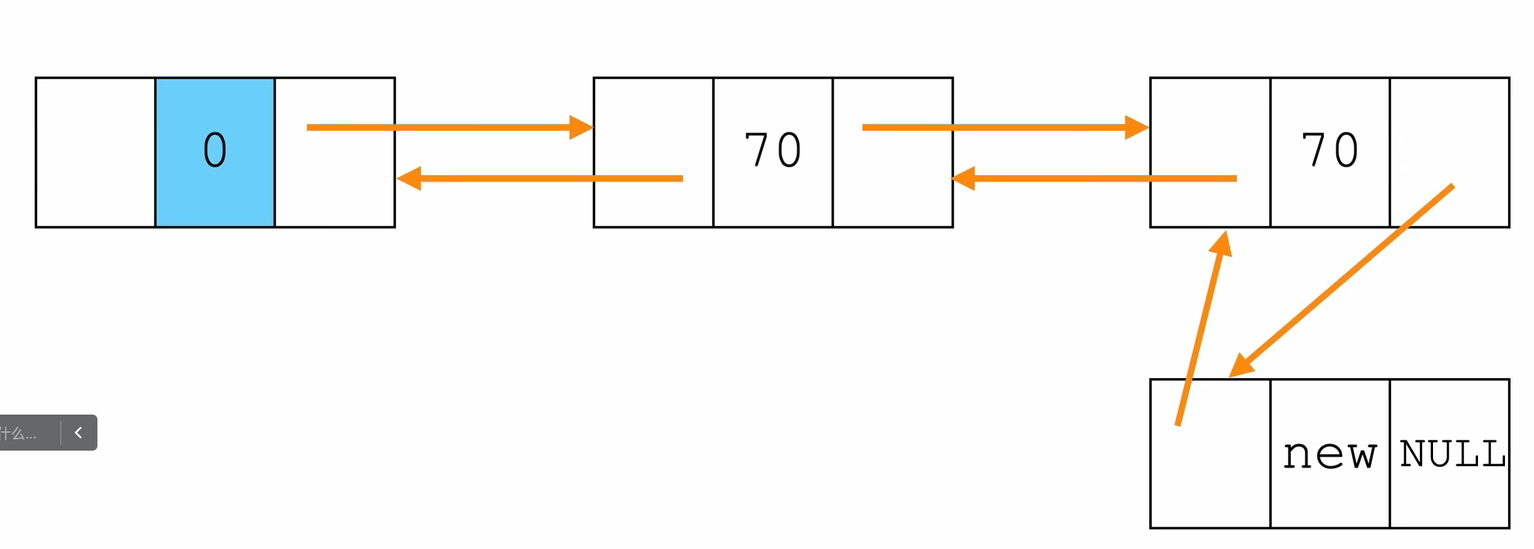
// 获取尾部节点
Node* get_tail(Node *L){
    Node *p=L;
    while (p->next!=NULL)
    {
        p=p->next;
    }
    return p;
}
// 尾插法
Node* insertTail(Node *tail,ElemType e){
    Node *p=(Node*)malloc(sizeof(Node));
    p->data=e;
    p->prev=tail;
    tail->next=p;
    p->next=NULL;
    return p;
}
  1. 在指定位置插入数据

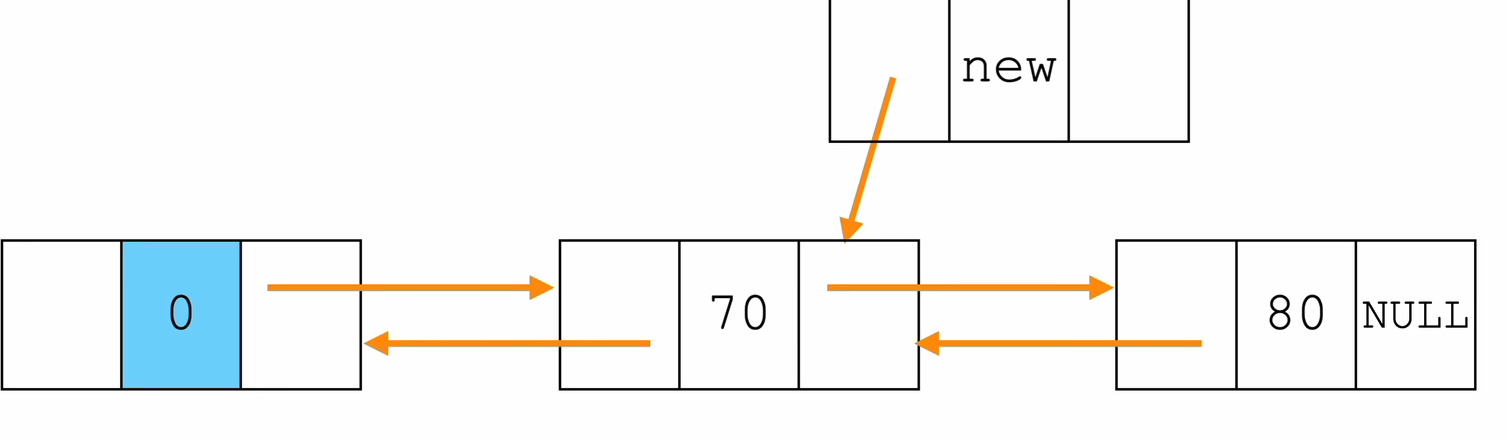
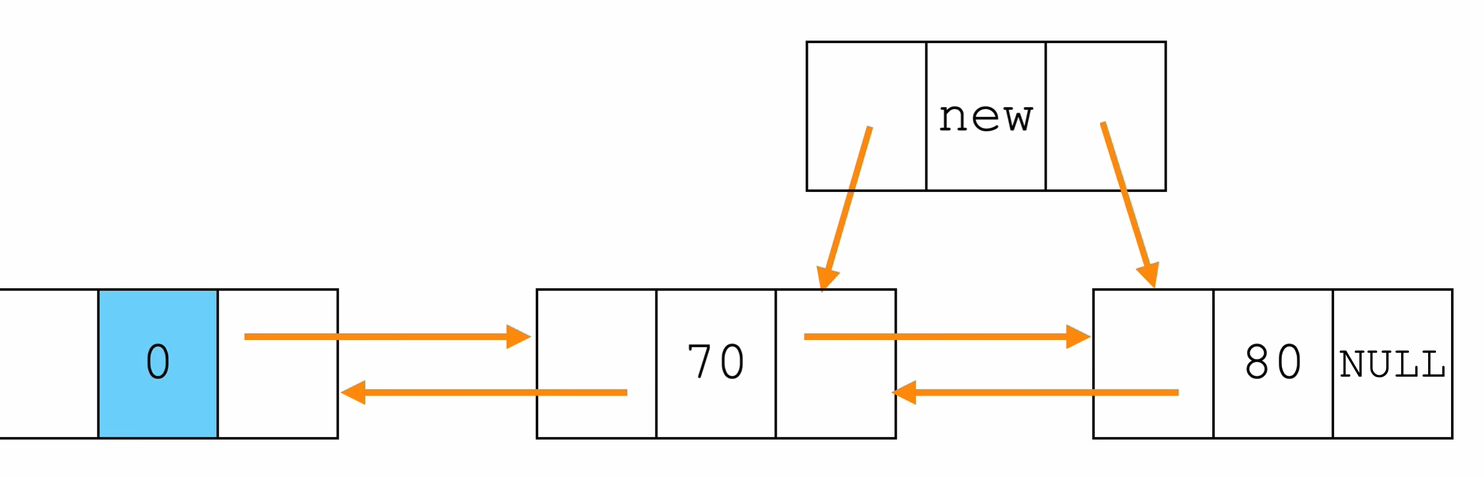
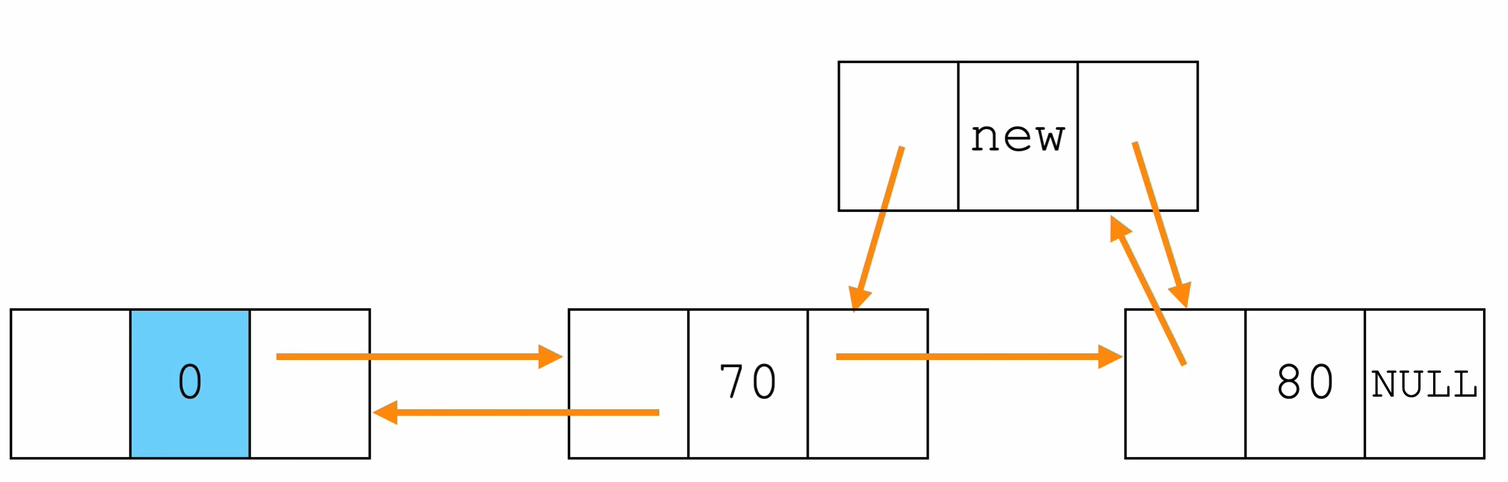
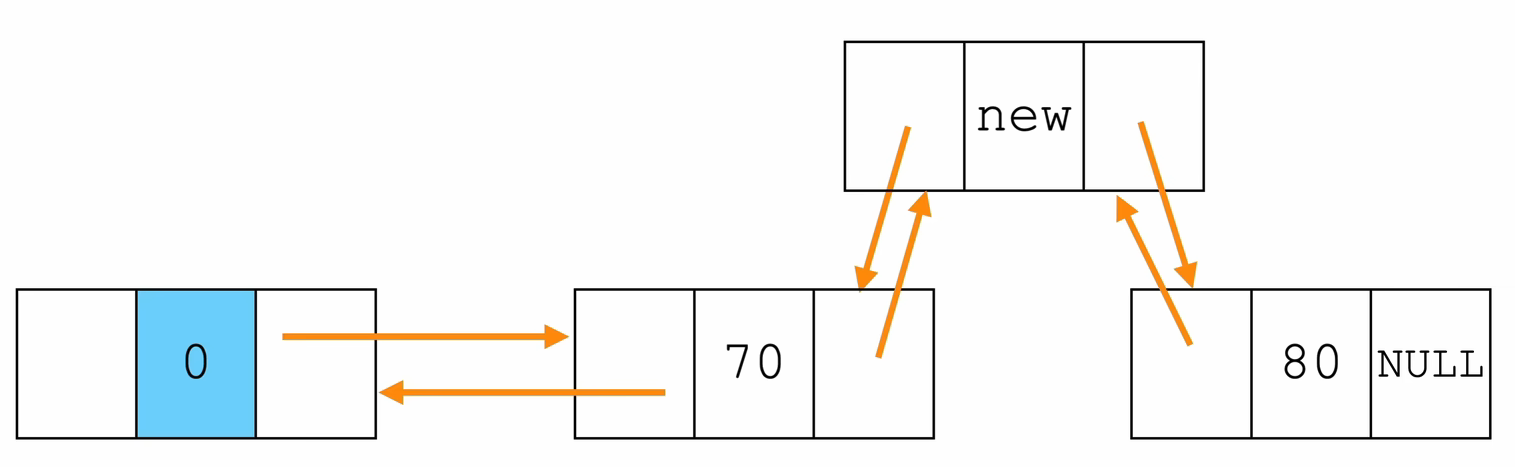
// 指定位置插入
int insertNode(Node *L,int pos,ElemType e){
    Node *p=L;
    int i=0;
    while (i<pos-1)
    {
        p=p->next;
        i++;
        if (p==NULL)
        {
            return 0;
        }
    }
    Node *q= (Node*)malloc(sizeof(Node));
    q->data=e;
    q->prev=p;
    q->next=p->next;
    p->next->prev=q;
    p->next=q;
    return 1;
}
  1. 删除节点
  • 找到要删除节点的前置节点p
  • 用指针q记录要删除的节点
  • 通过改变p的后置节点及要删除节点的下一个节点的前驱实现删除
  • 释放删除节点的空间

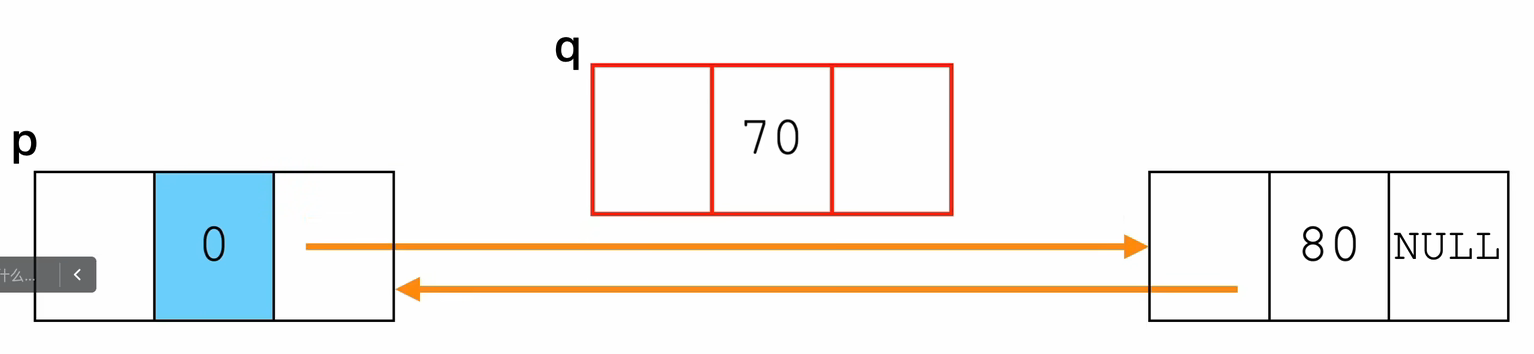
int deleteNode(Node *L,int pos){
    Node *p=L;
    int i=0;
    while (i<pos-1)
    {
        p=p->next;
        i++;
        if (p==NULL)
        {
            return 0;
        }
    }
    if (p->next==NULL)
    {
        printf("要删除的位置错误\n");
        return 0;
    }
    Node *q=p->next;
    p->next=q->next;
    q->next->prev=p;
    free(q);
    return 1;
}

汇总:

// 双向链表
#include <stdio.h>
#include <stdlib.h>

typedef int ElemType;
typedef struct node
{
    ElemType data;
    struct node *prev,*next;
}Node;


// 初始化链表
Node* initList(){
    Node *head=(Node*)malloc(sizeof(Node));
    head->data=0;
    head->next=NULL;
    head->prev=NULL;
    return head;
}

// 头插法
// 在 双向链表 的 头结点 L 之后，插入一个新节点 p
int insertHead(Node* L,ElemType e){
    Node *p=(Node*)malloc(sizeof(Node));
    p->data=e;
    p->prev=L;
    p->next=L->next;
// 如果原本链表不为空（也就是 头节点L之后确实还有节点），
// 那么原来第一个节点（即 L->next）的 prev 指针，
// 要从原来的 L 改成现在的 p
    if (L->next!=NULL)
    {
        L->next->prev=p;
    }
    L->next=p;
    return 1;
}

// 遍历
void listNode(Node* L){
      Node *p=L->next;
      while (p!=NULL)
      {
        printf("%d ",p->data);
        p=p->next;
      }
      printf("\n");
}
// 获取尾部节点
Node* get_tail(Node *L){
    Node *p=L;
    while (p->next!=NULL)
    {
        p=p->next;
    }
    return p;
}
// 尾插法
Node* insertTail(Node *tail,ElemType e){
    Node *p=(Node*)malloc(sizeof(Node));
    p->data=e;
    p->prev=tail;
    tail->next=p;
    p->next=NULL;
    return p;
}
// 指定位置插入
int insertNode(Node *L,int pos,ElemType e){
    Node *p=L;
    int i=0;
    while (i<pos-1)
    {
        p=p->next;
        i++;
        if (p==NULL)
        {
            return 0;
        }
    }
    Node *q= (Node*)malloc(sizeof(Node));
    q->data=e;
    q->prev=p;
    q->next=p->next;
    p->next->prev=q;
    p->next=q;
    return 1;
}

// 删除节点
int deleteNode(Node *L,int pos){
    Node *p=L;
    int i=0;
    while (i<pos-1)
    {
        p=p->next;
        i++;
        if (p==NULL)
        {
            return 0;
        }
    }
    if (p->next==NULL)
    {
        printf("要删除的位置错误\n");
        return 0;
    }
    Node *q=p->next;
    p->next=q->next;
    q->next->prev=p;
    free(q);
    return 1;
}

// 释放链表
void freeList(Node *L){
    Node *p=L->next;
    Node *q;
    while (p!=NULL)
    {
        q=p->next;
        free(p);
        p=q;
    }
    L->next=NULL;
}

int main(){
    Node *list=initList();
    insertHead(list,10);
    insertHead(list,20);
    insertHead(list,30);
    listNode(list);

    Node *tail=get_tail(list);
    tail=insertTail(tail,10);
    tail=insertTail(tail,20);
    tail=insertTail(tail,30);
    listNode(list);

    insertNode(list,2,15);
    listNode(list);

    deleteNode(list,2);
    listNode(list);
}

至此,线性表已全部讲完

顺序表VS链表

比较项目存储结构顺序表链表
空间存储空间预先分配，会出现闲置或溢出现象动态分配，不会出现存储空间闲置或溢出现象
存储密度不用为表示节点间的逻辑关系而增加额外的存储，存储密度等于1需要借助指针来体现元素间的逻辑关系，存储密度小于1
时间存取元素随机存取，按位置访问元素的时间复杂度为 O(1)顺序存取，按位置访问元素时间复杂度为 O(n)
插入、删除平均移动约表中一半元素，时间复杂度为 O(n)不需要移动元素，确定插入、删除位置后，时间复杂度为 O(1)
适用情况1）表长变化不大，且能事先确定变化的范围； 2）很少进行插入或删除操作，经常按位置查找元素序号访问数据元素。1）长度变化较大； 2）频繁进行插入或删除操作。

做个题

  1. 第一题

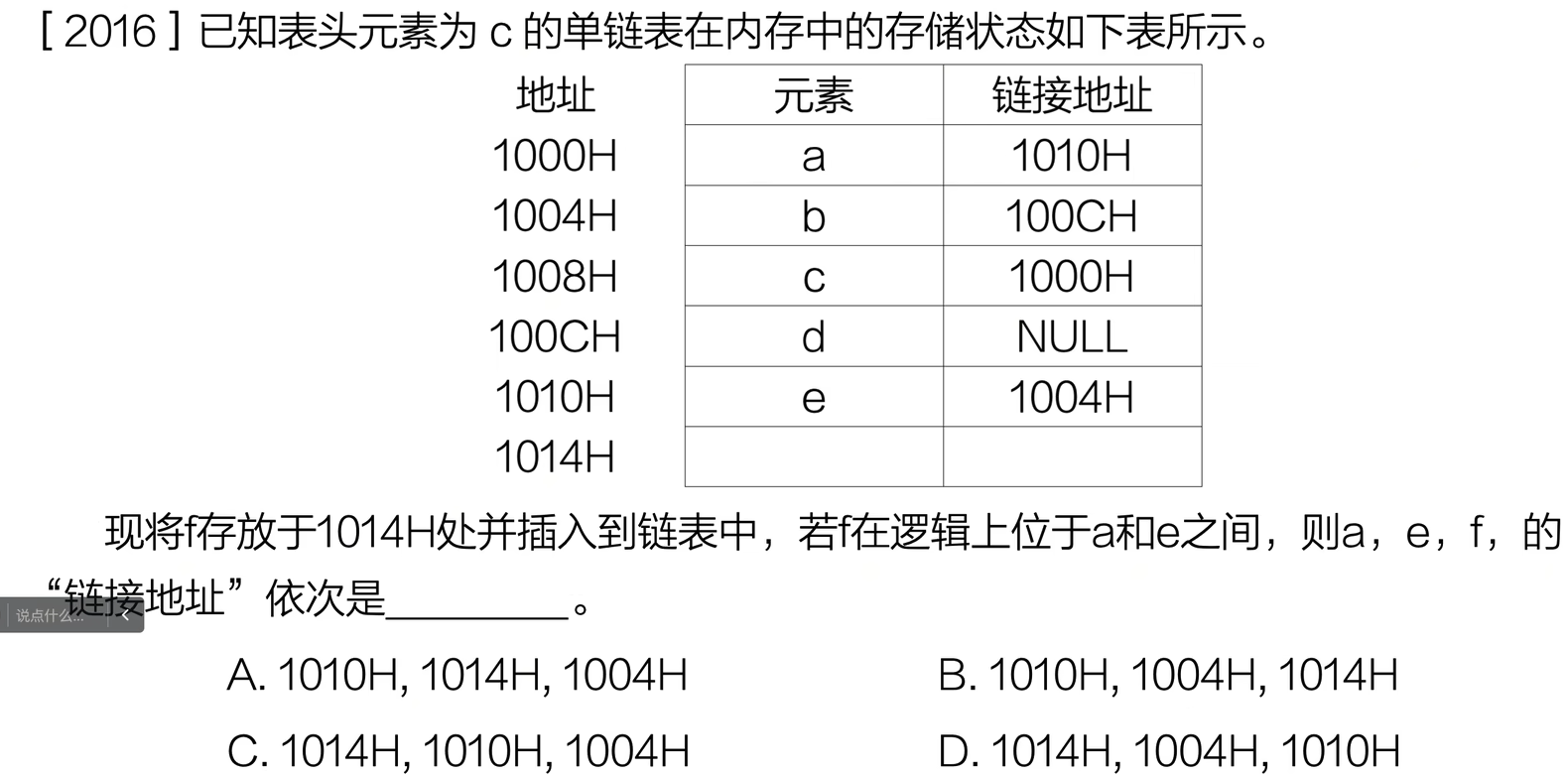
链接地址就是next

答案是D

  1. 第二题

答案:D

  1. 第三题

注意!链表可能就一个头节点一个尾节点

答案:D

!!!也可能p和q是同一个节点


3.栈

栈（stack）是限定仅在表尾进行插入或删除操作的线性表。因此对栈来说，表尾端有其特殊含义，称为栈顶（top），相应地，表头端称为栈底（bottom）。不含元素的空表称为空栈

假设 S = (a₁, a₂, ⋯, aₙ)，则称 a₁ 为栈底元素，aₙ 为栈顶元素。栈中元素按 a₁, a₂, ⋯, aₙ 的次序进栈，退栈的第一个元素应为栈顶元素。换句话说，栈的修改是按照后进先出的原则进行的。因此，栈又称为后进先出（Last In First Out，LIFO）的线性表

先进后出,后进先出

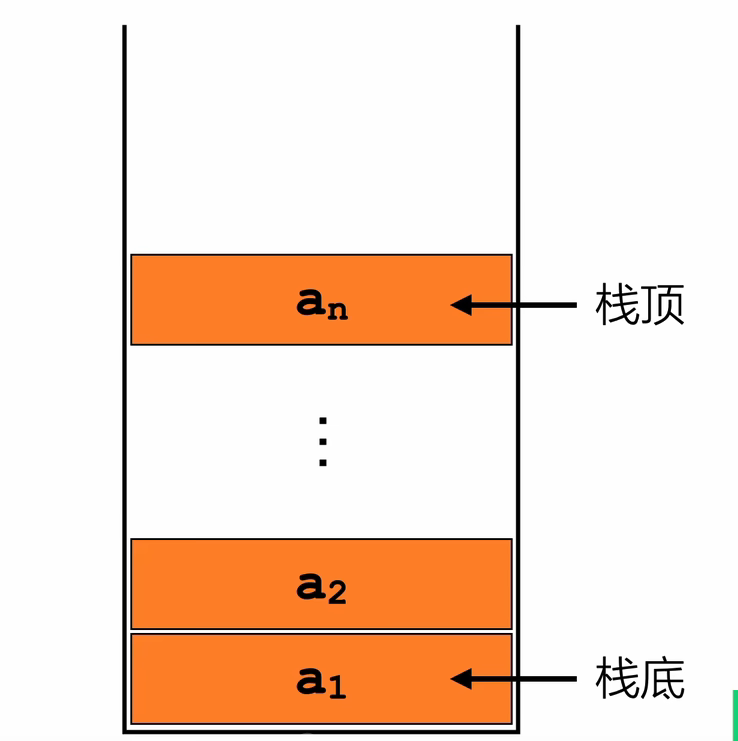
栈是限制插入和删除操作只能在一个位置进行的表,该位置是表的末端,叫做栈顶(top).对栈的基本操作有进栈(push)和出栈(Pop),前者表示插入,后者则是删除最后插入的元素

栈的顺序结构实现

  1. 初始化
#define MAXSIZE 100
typedef int ElemType;
typedef struct 
{
    ElemType data[MAXSIZE];
    int top;
}Stack;
void initStack(Stack *s){
    s->top=-1;
}

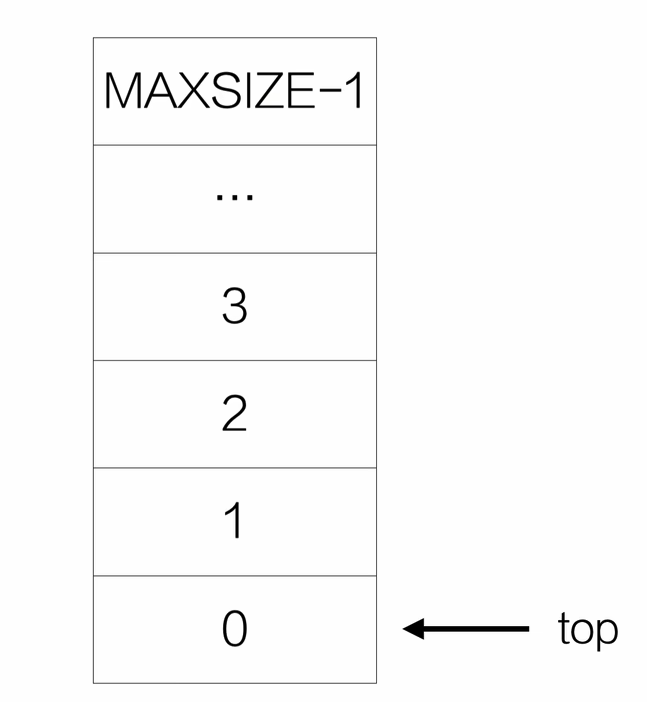
  1. 判断栈是否为空
int isEmpty(Stack *s){
    if (s->top==-1)
    {
        printf("空的\n");
        return 1;
    }
    else{
        return 0;
    }
}
  1. 进栈/压栈
int push(Stack *s,ElemType e){
    if (s->top>=MAXSIZE-1)
    {
        printf("满了\n");
        return 0;
    }
    s->top++;
    s->data[s->top]=e;
    return 1;
}
  1. 出栈

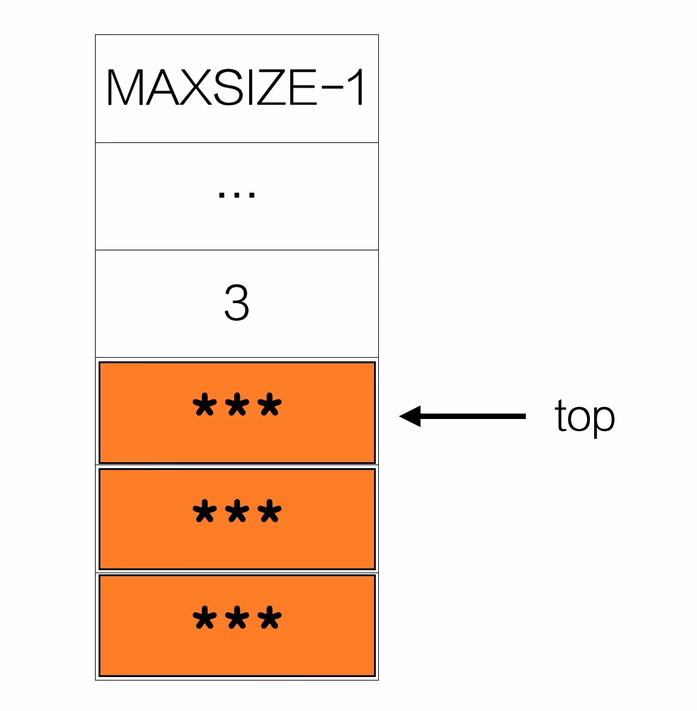
ElemType pop(Stack *s,ElemType *e){
    if (s->top==-1)
    {
        printf("空的\n");
        return 0;
    }
    *e=s->data[s->top];
    s->top--;
    return 1;
}
  1. 获取栈顶元素
int getTop(Stack *s,ElemType *e){
    if (s->top==-1)
    {
        printf("空的\n");
        return 0;
    }
    *e=s->data[s->top];
    return 1;
}

汇总

#include <stdio.h>
#include <stdlib.h>
#define MAXSIZE 100
typedef int ElemType;
typedef struct 
{
    ElemType data[MAXSIZE];
    int top;
}Stack;
void initStack(Stack *s){
    s->top=-1;
}
// 判断栈是否为空
int isEmpty(Stack *s){
    if (s->top==-1)
    {
        printf("空的\n");
        return 1;
    }
    else{
        return 0;
    }
}
// 压栈
int push(Stack *s,ElemType e){
    if (s->top>=MAXSIZE-1)
    {
        printf("满了\n");
        return 0;
    }
    s->top++;
    s->data[s->top]=e;
    return 1;
}

// 出栈
ElemType pop(Stack *s,ElemType *e){
    if (s->top==-1)
    {
        printf("空的\n");
        return 0;
    }
    *e=s->data[s->top];
    s->top--;
    return 1;
}


// 获取栈顶元素
int getTop(Stack *s,ElemType *e){
    if (s->top==-1)
    {
        printf("空的\n");
        return 0;
    }
    *e=s->data[s->top];
    return 1;
}

int main(){
    Stack s;
    initStack(&s);
    push(&s,10);
    push(&s,20);
    push(&s,30);
    ElemType e;
    pop(&s,&e);
    printf("%d\n",e);
    getTop(&s,&e);
    printf("%d\n",e);
}
  1. 栈的顺序结构的初始化
#define MAXSIZE 100
typedef int ElemType;
typedef struct 
{
    ElemType *data;  //指针指向堆内存一片连续的空间
    int top;
}Stack;

Stack* initStack(){
    Stack *s=(Stack*)malloc(sizeof(Stack));
    s->data=(ElemType*)malloc(sizeof(ElemType)*MAXSIZE);
    s->top=-1;
    return s;
}

栈的链式实现

typedef int ElemType;
typedef struct stack
{
    ElemType data;
    struct stack *next;
}Stack;

尾节点是栈底

头节点的下一个节点就是栈顶

压栈其实就是头插法

栈空就是只有一个头节点,也就是头节点的next是否为NULL

获取栈顶数据—找头节点的下一个节点的data

  1. 初始化

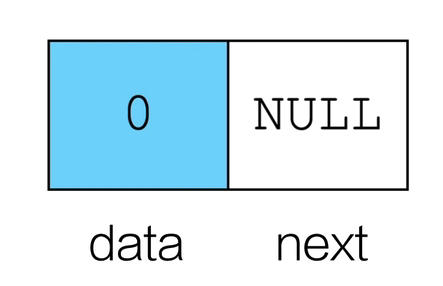
Stack* initStack(){
    Stack* s=(Stack*)malloc(sizeof(Stack));
    s->data=0;
    s->next=NULL;
    return s;
}
  1. 判断栈是否为空
int isEmpty(Stack *s){
    if (s->next==NULL)
    {
        printf("空的\n");
        return 0;
    }
    else{
        return 0;
    }
}
  1. 进栈/压栈

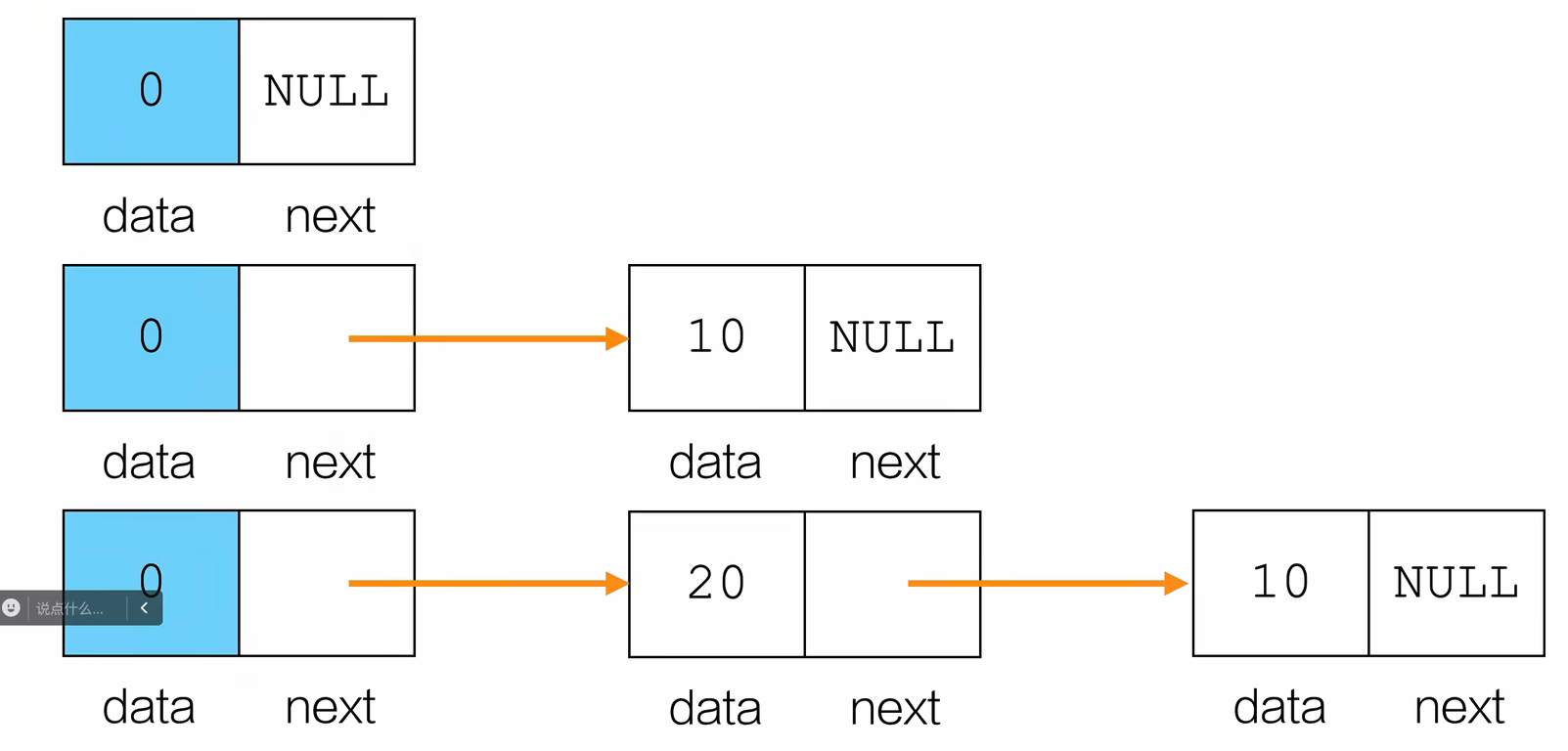
int push(Stack *s,ElemType e){
    Stack *p=(Stack*)malloc(sizeof(Stack));
    p->data=e;
    p->next=s->next;
    s->next=p;
    return 1;
}
  1. 出栈

删除头节点后的那一个节点的数据：

  • 找到头节点p
  • 用指针q记录要出栈的节点
  • 通过改变q的后继节点实现出栈

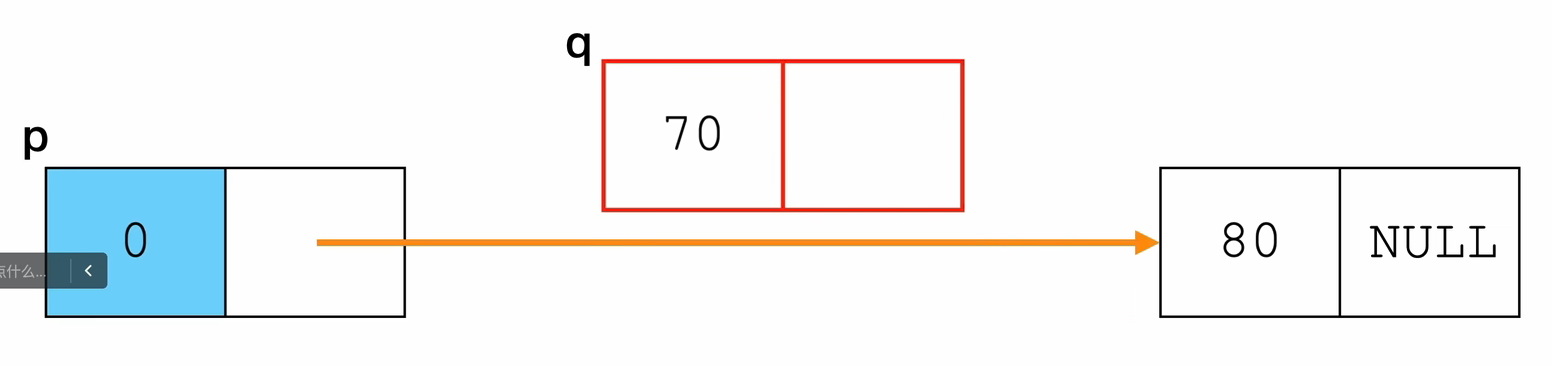
int pop(Stack *s,ElemType *e){
    if (s->next==NULL)
    {
        printf("空的\n");
        return 0;
    }
    *e=s->next->data;
    Stack *q=s->next;
    s->next=q->next;
    free(q);
    return 1;
}
  1. 获取栈顶元素
int getTop(Stack *s,ElemType *e){
    if (s->next==NULL)
    {
        printf("空的\n");
        return 0;
    }
    *e=s->next->data;
    return 1;
}

汇总：

// 栈的链式结构实现
#include <stdio.h>
#include <stdlib.h>
typedef int ElemType;
typedef struct stack
{
    ElemType data;
    struct stack *next;
}Stack;

Stack* initStack(){
    Stack* s=(Stack*)malloc(sizeof(Stack));
    s->data=0;
    s->next=NULL;
    return s;
}

// 判断栈是否为空
int isEmpty(Stack *s){
    if (s->next==NULL)
    {
        printf("空的\n");
        return 0;
    }
    else{
        return 0;
    }
}

//  进栈/压栈
int push(Stack *s,ElemType e){
    Stack *p=(Stack*)malloc(sizeof(Stack));
    p->data=e;
    p->next=s->next;
    s->next=p;
    return 1;
}

// 出栈
int pop(Stack *s,ElemType *e){
    if (s->next==NULL)
    {
        printf("空的\n");
        return 0;
    }
    *e=s->next->data;
    Stack *q=s->next;
    s->next=q->next;
    free(q);
    return 1;
}

// 获取栈顶元素
int getTop(Stack *s,ElemType *e){
    if (s->next==NULL)
    {
        printf("空的\n");
        return 0;
    }
    *e=s->next->data;
    return 1;
}

int main(){
    Stack *s=initStack();
    push(s,10);
    push(s,20);
    push(s,30);
    ElemType e;
    pop(s,&e);
    printf("%d\n",e);

    getTop(s,&e);
    printf("%d\n",e);
}

4.队列

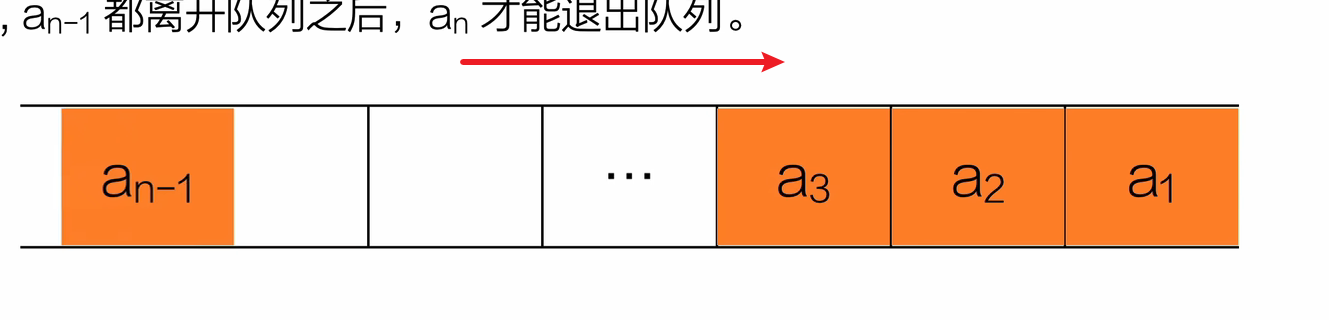
队列（queue）是一种先进先出（First In First Out，FIFO）的线性表。它只允许在表的一端进行插入，而在另一端删除元素。在队列中，允许插入的一端称为队尾（rear），允许删除的一端则称为队头（front）。假设队列为 q = (a₁, a₂, ⋯, aₙ)，那么，a₁ 就是队头元素，aₙ 就是队尾元素。队列中的元素是按照 a₁, a₂, ⋯, aₙ 的顺序进入的，退出队列也只能按照这个次序依次退出，也就是说，只有在 a₁, a₂, ⋯, aₙ₋₁ 都离开队列之后，aₙ 才能退出队列。

  1. 初始化

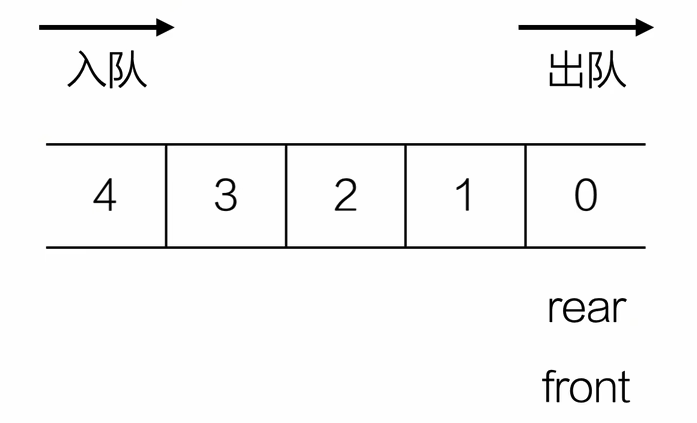
typedef int ElemType;
typedef struct 
{
    ElemType data[MAXSIZE];
    int front;
    int rear;
}Queue;

void initQueue(Queue *Q){
    Q->front=0;
    Q->rear=0;
}
  1. 判断队列是否为空

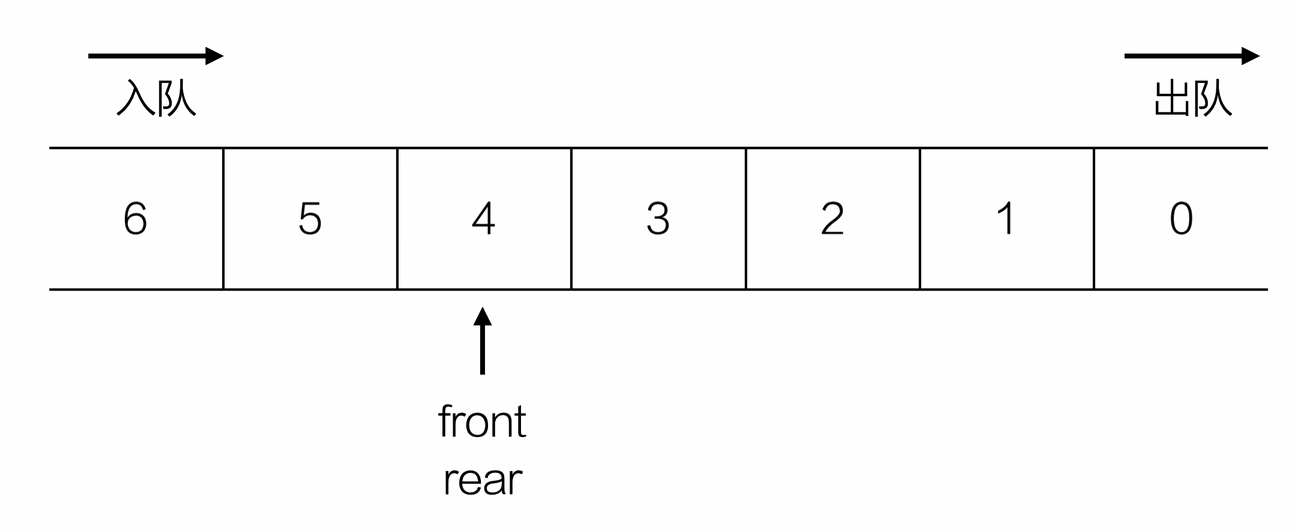
int isEmpty(Queue *Q){
    if (Q->front==Q->rear)
    {
        printf("空的\n");
        return 1;
    }
    else{
        return 0;
    }
}
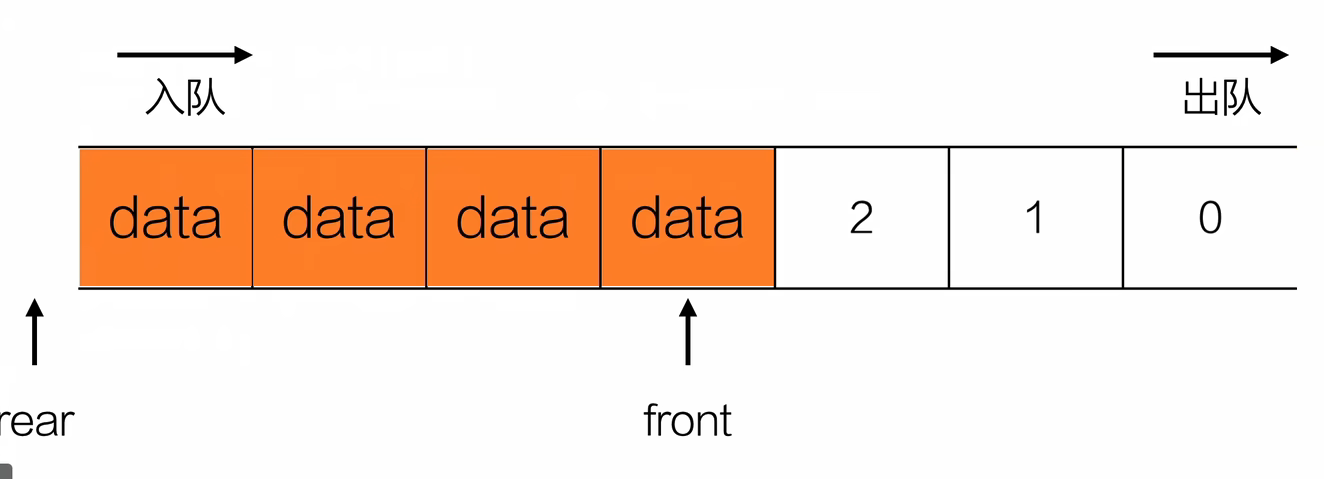
  1. 入队

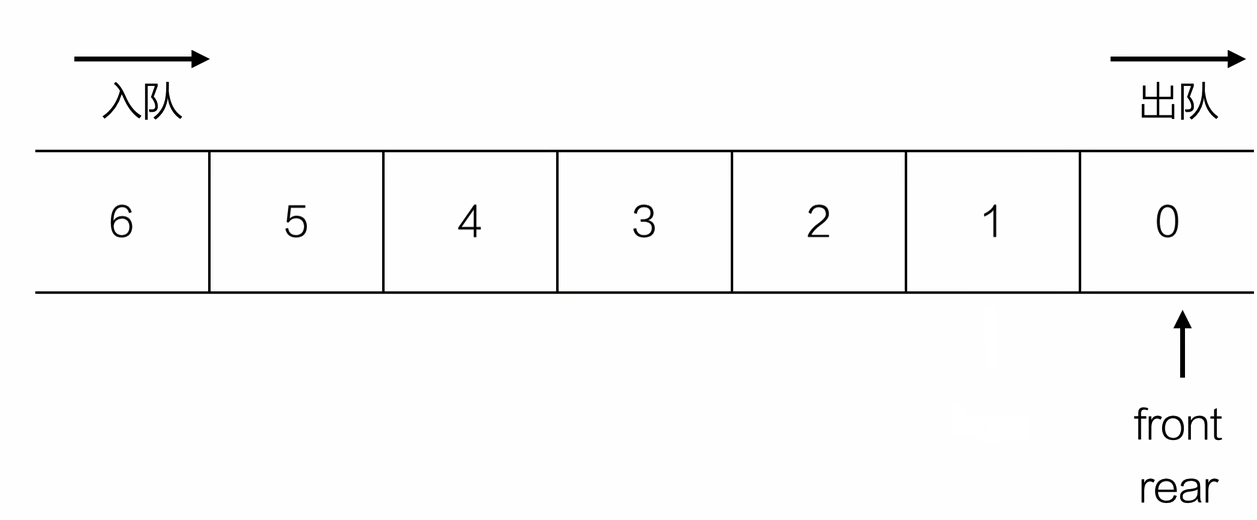
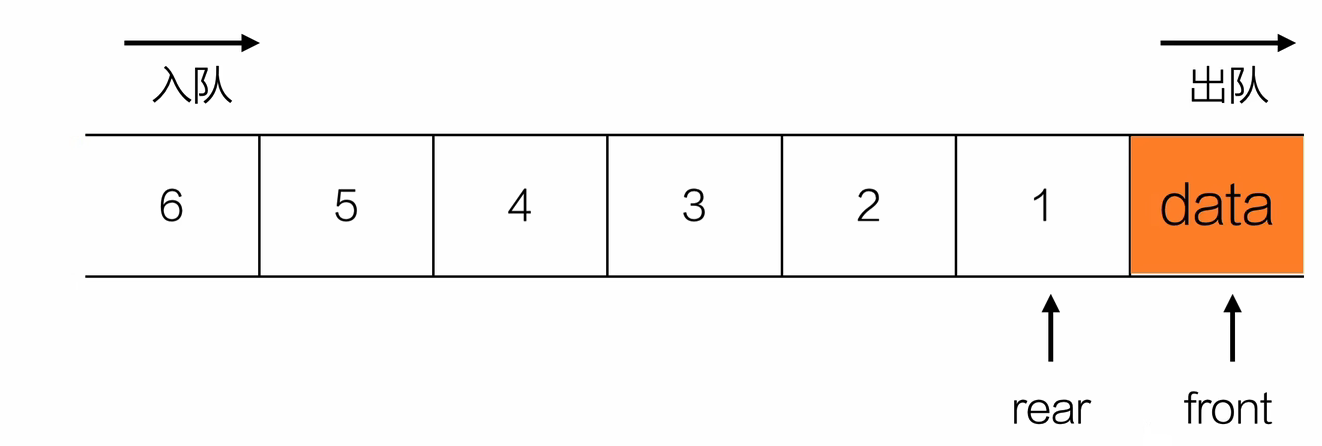
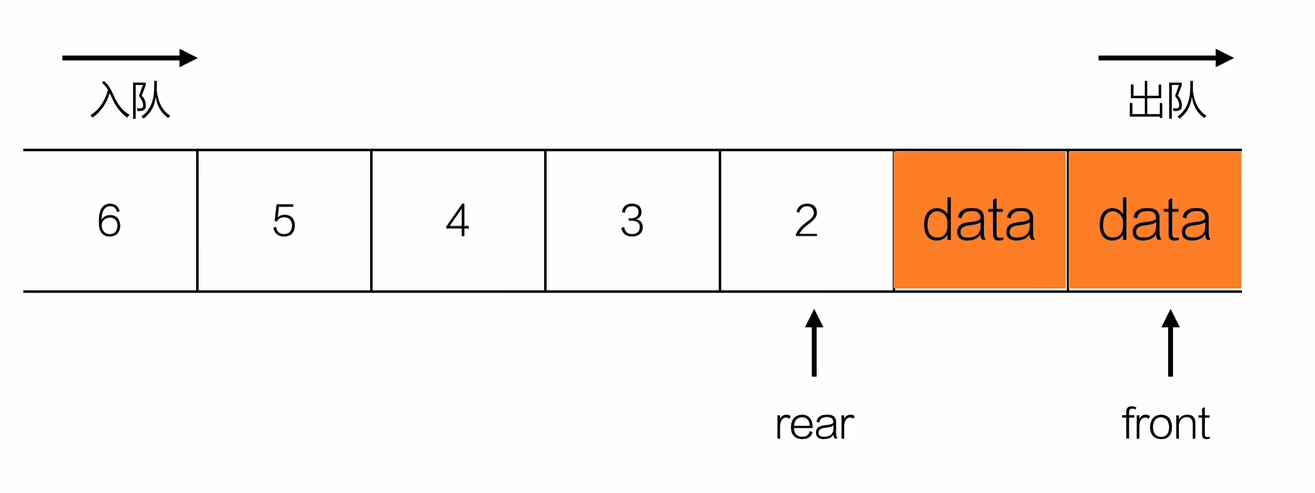
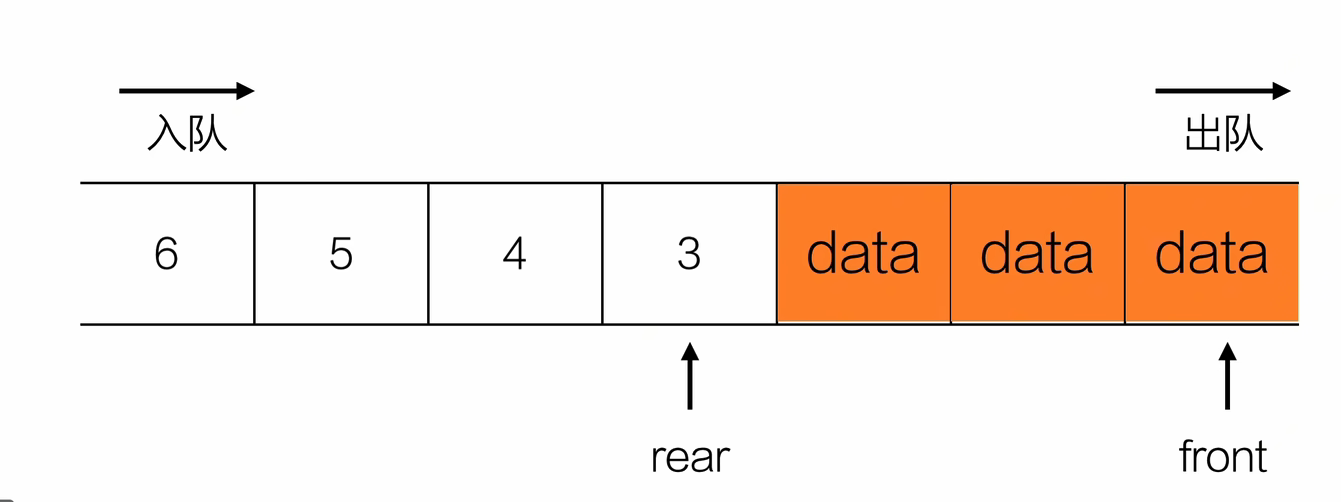
int equeue(Queue *Q,ElemType e){
    if (Q->rear>=MAXSIZE)
    {
        // 发现对尾到头了
        if (!queueFull(Q))
        {
            return 0;
        }
    }
    Q->data[Q->rear]=e;
    Q->rear++;
    return 1;
}
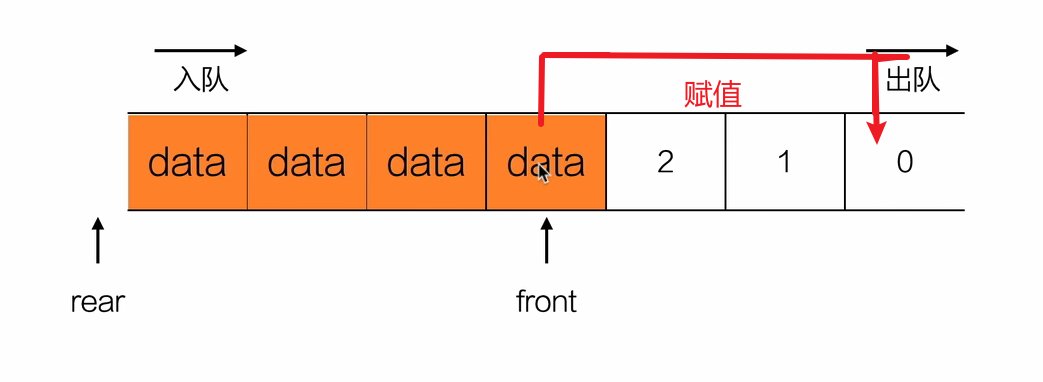
  1. 出队

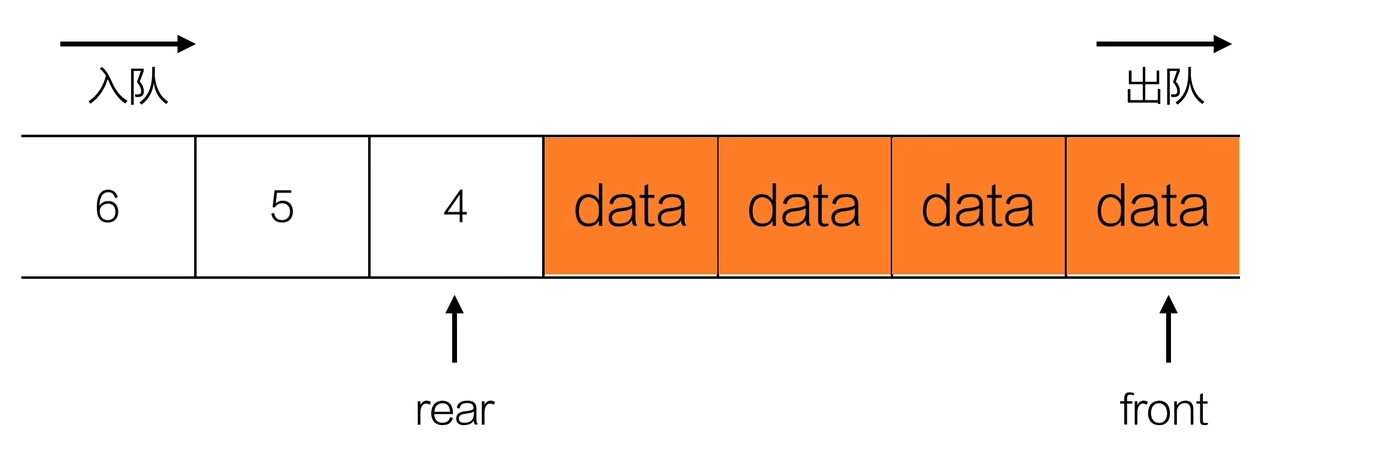
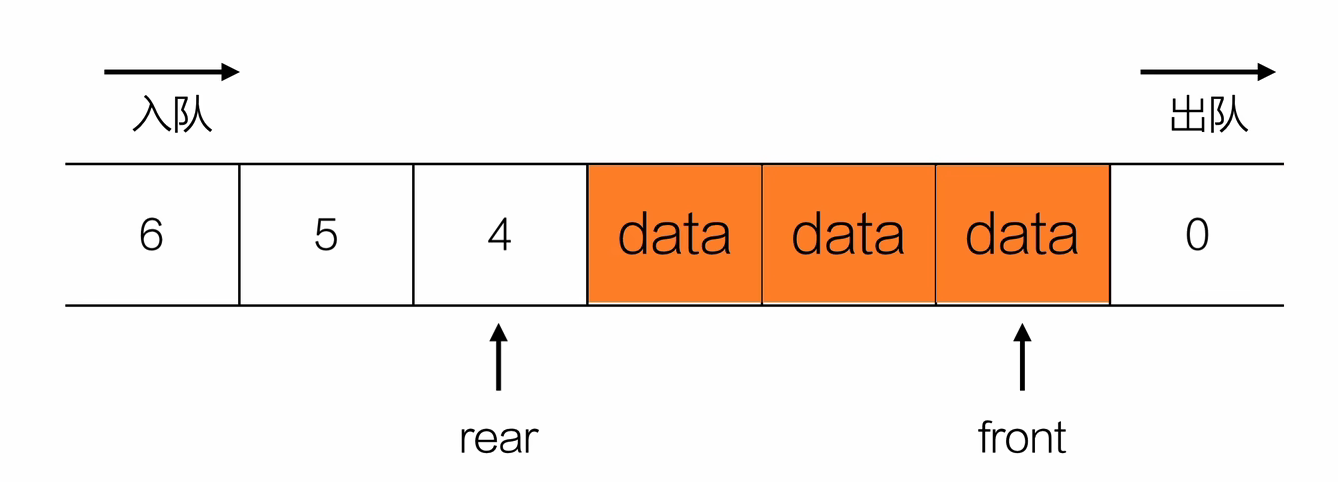
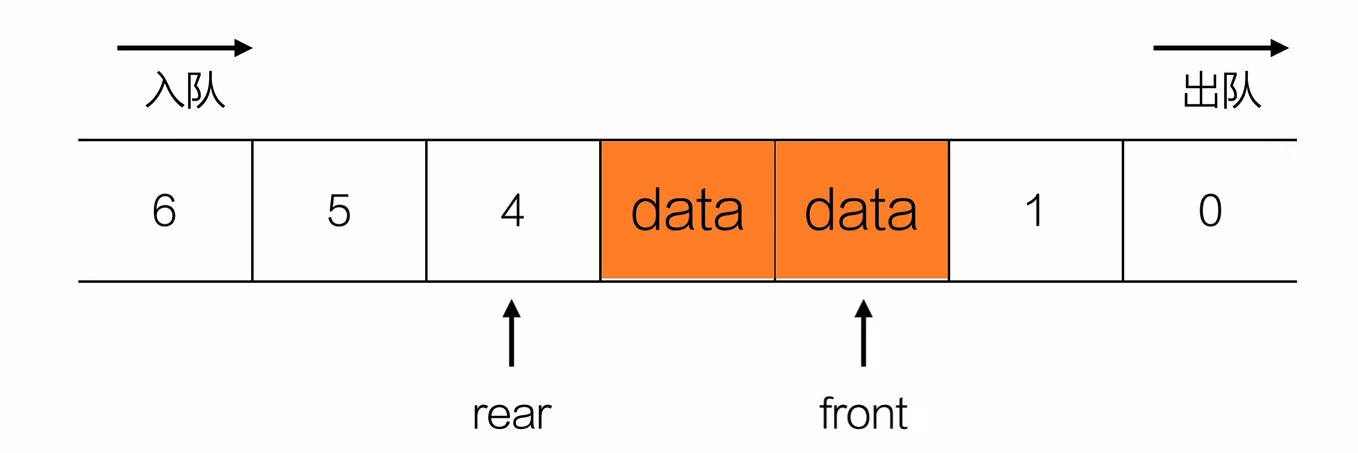
ElemType dequeue(Queue *Q){
    if (Q->front==Q->rear)
    {
        printf("空的\n");
        return 0;
    }
    ElemType e=Q->data[Q->front];
    Q->front++;
    return e;
}
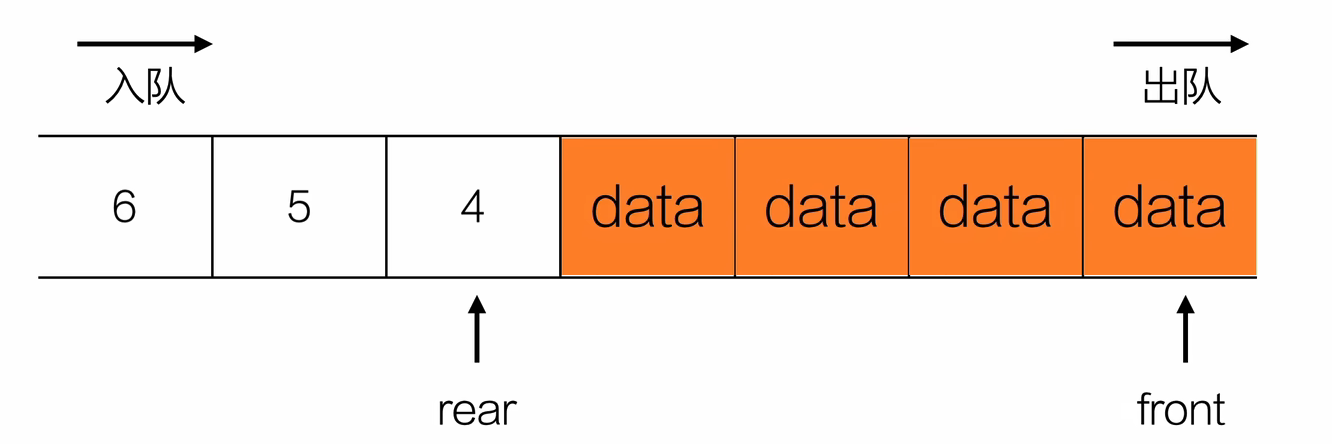
  1. 对尾满了，调整队列
int queueFull(Queue *Q){
    if (Q->front>0)
    {
        int step=Q->front;
        for (int i = Q->front; i <= Q->rear; ++i)
        {
            Q->data[i-step]=Q->data[i];
        }
        Q->front=0;
        Q->rear=Q->rear-step;
        return 1;
    }
    else{
        printf("真的满了\n");
        return 0;
    }
}

  1. 获取对头元素
int getHead(Queue *Q,ElemType *e){
    if (Q->front==Q->rear)
    {
        printf("空的\n");
        return 0;
    }
    *e=Q->data[Q->front];
    return 1;
}

汇总：

#include <stdio.h>
#include <stdlib.h>
#define MAXSIZE 100
typedef int ElemType;
typedef struct 
{
    ElemType data[MAXSIZE];
    int front;
    int rear;
}Queue;

void initQueue(Queue *Q){
    Q->front=0;
    Q->rear=0;
}
// 预声明，避免隐式声明告警
int queueFull(Queue *Q);


// 判断队列是否为空
int isEmpty(Queue *Q){
    if (Q->front==Q->rear)
    {
        printf("空的\n");
        return 1;
    }
    else{
        return 0;
    }
}


// 出队
ElemType dequeue(Queue *Q){
    if (Q->front==Q->rear)
    {
        printf("空的\n");
        return 0;
    }
    ElemType e=Q->data[Q->front];
    Q->front++;
    return e;
}

// 入队
int equeue(Queue *Q,ElemType e){
    if (Q->rear>=MAXSIZE)
    {
        if (!queueFull(Q))
        {
            return 0;
        }
    }
    Q->data[Q->rear]=e;
    Q->rear++;
    return 1;
}

// 队尾满了，调整队列
int queueFull(Queue *Q){
    if (Q->front>0)
    {
        int step=Q->front;
        for (int i = Q->front; i <= Q->rear; ++i)
        {
            Q->data[i-step]=Q->data[i];
        }
        Q->front=0;
        Q->rear=Q->rear-step;
        return 1;
    }
    else{
        printf("真的满了\n");
        return 0;
    }
}

// 获取队头元素
int getHead(Queue *Q,ElemType *e){
    if (Q->front==Q->rear)
    {
        printf("空的\n");
        return 0;
    }
    *e=Q->data[Q->front];
    return 1;
}

int main(){
    Queue q;
    initQueue(&q);

    equeue(&q,10);
    equeue(&q,20);
    equeue(&q,30);
    equeue(&q,40);
    equeue(&q,50);
    printf("%d\n",dequeue(&q));
    printf("%d\n",dequeue(&q));
    ElemType e;
    getHead(&q,&e);
    printf("%d\n",e);
}
数据结构与算法--（链表，栈，队列）
qq_43710889的博客
04-22 1261
数据结构与算法–（链表，栈，队列） 文章目录数据结构与算法--（链表，栈，队列）链表定义单向链表功能:1.头部添加元素2.尾部添加元素3.指定位置添加元素4.删除节点5.查找节点是否存在6.判断链表是否为空7.当前链表的长度8.遍历链表全部代码粘贴双向链表功能:1.头部添加元素2.尾部添加元素3.指定位置添加元素4.删除节点5.查找节点是否存在6.判断链表是否为空7.当前链表的长度8.遍历链表全部代码粘贴栈（stack）栈的实现队列（queue）队列的实现 链表 定义 链表：是一种常见的数据结构，是一种线性
算法与数据结构python实现-栈、链表、队列
Sun123234的博客
01-17 890
算法与数据结构python实现-栈、链表、队列
数据结构与算法--链表
m0_71155220的博客
08-04 1581
* 链表存放数据的类型 *//* 链表节点类型 *///存放数据空间//存放下一个节点地址}linknode。
数据结构与算法-双向链表
m0_62988332的博客
02-27 1681
总之，双向链表作为一个既有单链表的动态特性又增加了双向访问能力的数据结构，其在实际应用中扮演着举足轻重的角色。通过对双向链表的深入理解和熟练运用，开发者能够更好地优化算法性能，提高程序设计的灵活性和效率。
【数据结构】链表--双向链表
Skrrapper的博客
05-21 1110
双向链表每个元素都是一个对象，每个对象包括一个数据域和两个指针域next和prev。我们知道，单链表可以从后往前轻松的前进，但是它很难实现后退。它一般只能从头到尾或者从尾到头。那么当我们需要实现更加灵活的操作时，就可以使用双向链表：拥有两个指针域，一个指向前驱节点，一个指向后继节点，在操作时既可以前进也可以后退，灵活性大大提高。双向链表的操作普遍上比单向链表简单，因为它多了一个指针域所以操作的灵活性大大提高。如果头指针指向自己，那么此时的链表就自然是一个空表，完成双向链表的初始化。
数据结构与算法学习笔记
热门推荐
ityqing的博客
09-25 34万+
本文是王争老师的《算法与数据结构之美》的学习笔记，详细内容请看王争的专栏。有不懂的地方指出来，我做修改。 数据结构与算法思维导图 数据结构指的是“一组数据的存储结构”，算法指的是“操作数据的一组方法”。 数据结构是为算法服务的，算法是要作用再特定的数据结构上的。 最常用的数据结构预算法: 数据结构：数组、链表、栈、队列、散列表、二叉树‘、堆、跳表、图、Tire树 算法： 递归...
C语言实现基础数据结构：链表、栈与队列详解
vvilkin的学习备忘
04-30 1257
数据结构是计算机科学的核心基础之一，它决定了数据的组织、存储和操作方式。在C语言中，我们可以通过指针和结构体等特性灵活地实现各种数据结构。本文将详细介绍三种基础数据结构——链表、栈和队列的C语言实现，包括它们的原理、实现方式以及应用场景。
Python数据结构与算法-数据结构(列表、栈、队列、链表)
little_limin的博客
04-04 4149
python的数据结构与算法
【Go 数据结构】链表，栈与队列
weixin_55818116的博客
05-05 1582
Go语言实现常见的数据结构，这一系列你一定不要错过，快来学习吧，教你如何使用Go语言实现链表，队列和栈。
数据结构：栈、队列、链表
Made In SQL
07-15 675
栈是一种遵循**后进先出（LIFO）**原则的线性数据结构。
算法-数据结构和算法-8-双向链表.rar
09-16
本资源"算法-数据结构和算法-8-双向链表.rar"聚焦于一种常用的数据结构——双向链表。双向链表是链式存储结构的一种，与单向链表相比，它具有更多的灵活性和便利性。 双向链表的每个节点不仅包含数据元素，还包含两...
数据结构算法集---C++语言实现.rar_queue stack_堆栈 栈_数据结构 队列_链表_队列
07-15
在这个C++实现的数据结构算法集中，主要涉及了几个核心概念：队列、堆栈和链表，这些都是数据组织和操作的基本工具。 首先，让我们来看看堆栈（Stack）。堆栈是一种后进先出（LIFO）的数据结构，它的操作类似于日常...
Java算法实例-双向链表操作
08-22
在编程领域，数据结构与算法是基础且至关重要的部分，它们直接影响到程序的效率和设计。本实例聚焦于Java中的一个重要数据结构——双向链表，它在很多场景下都有着广泛的应用。双向链表与单链表相比，其独特之处在于...
《算法与数据结构》第四章：栈与队列-链队列C语言实现
01-08
算法与数据结构是计算机科学的基础，其中栈与队列作为两种重要的数据结构，在软件开发与系统设计中扮演着关键角色。栈是一种后进先出（LIFO）的数据结构，而队列则是一种先进先出（FIFO）的数据结构。在C语言实现中...
java学习：四大排序
t2786024916的博客
10-03 490
开始的时候我们定义一个最小值j，j指针指向该值的序号如图j=0；定义一个新指针i去寻找剩余的值中的最小值。2.对每一对相邻元素做同样的工作，从开始第一对到结尾的最后一对；从数组第二个元素开始，将其视为待插入的元素，我们用j来指代，让改元素于前边的元素进行对比；开始定义一个最小值的位置，然后遍历剩余的n-1给元素找到一个小于这个值的与之交换。现在数组arr[0],arr[1]有序，将待排顺序数组arr[2]于前两个经行对比。3.重复以上步骤，直至完成。j自增1，这时就有一个有序的数，接下来重复该过程。
数据结构——优先级队列（堆）
最新发布
weixin_74163692的博客
10-04 985
优先级队列是一种特殊的队列，它根据元素的优先级决定出队顺序，优先级高的元素先出队。
数据结构预算法与图论
_realyin_的博客
10-02 250
数据结构是计算机存储、组织数据的方式，它直接决定了数据操作的效率与资源的利用率。更为复杂的结构如哈希表通过散列函数实现了近似常数时间的查找，而平衡二叉搜索树则在动态数据集中保持了元素的有序性与操作稳定性。理解不同数据结构的特性及其时间、空间复杂度，是设计高效算法的基础，能够帮助开发者针对特定问题选择最合适的工具，避免不必要的性能瓶颈。图的遍历算法，如广度优先搜索和深度优先搜索，是探索图结构的基础。动态规划通过存储子问题的解来避免重复计算，有效解决了具有最优子结构特点的问题，例如背包问题和最长公共子序列。
【数据结构】从零到精通：图解栈和队列的基本操作与应用！
persevereX的博客
10-03 867
想在面试中脱颖而出？ 掌握栈和队列是关键！本文将带你一站式精通这两大基础数据结构——栈 (LIFO) 和 队列 (FIFO)。涵盖顺序栈、链式栈、链队列和循环队列的完整代码，深入剖析它们的底层原理和设计权衡。从括号匹配到 BFS 算法，彻底理清它们的实战应用。如果你想用 O(1) 的效率解决问题，并用最健壮的代码巩固基础，这篇技术干货你绝不能错过！
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值