【数据结构与算法 | 灵神题单 | 遍历链表篇】力扣1290， 2058

1. 力扣1290：二进制链表转整数

1.1 题目：

给你一个单链表的引用结点 head。链表中每个结点的值不是 0 就是 1。已知此链表是一个整数数字的二进制表示形式。

请你返回该链表所表示数字的 十进制值 。

示例 1：

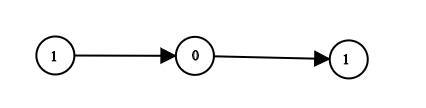
输入：head = [1,0,1]
输出：5
解释：二进制数 (101) 转化为十进制数 (5)

示例 2：

输入：head = [0]
输出：0

示例 3：

输入：head = [1]
输出：1

示例 4：

输入：head = [1,0,0,1,0,0,1,1,1,0,0,0,0,0,0]
输出：18880

示例 5：

输入：head = [0,0]
输出：0

提示：

• 链表不为空。
• 链表的结点总数不超过 30。
• 每个结点的值不是 0 就是 1。

1.2 思路：

用栈来记录链表的元素，由于栈的性质，最先弹栈的元素是末位，转换成10进制需要*1，其次弹栈的元素转换成10进制需要*2...直到栈空，将所有的值加起来返回。

1.3 题解：

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public int getDecimalValue(ListNode head) {
        Deque<Integer> stack = new LinkedList<>();
        while (head != null) {
            stack.push(head.val);
            head = head.next;
        }
        int m = 1;
        int sum = 0;
        while (!stack.isEmpty()){
            sum += m * stack.pop();
            m *= 2;
        }
        return sum;
    }
}

2. 力扣2058：找出临界点之间的最小和最大距离

2.1 题目：

链表中的 临界点 定义为一个 局部极大值点 或 局部极小值点 。

如果当前节点的值 严格大于 前一个节点和后一个节点，那么这个节点就是一个  局部极大值点 。

如果当前节点的值 严格小于 前一个节点和后一个节点，那么这个节点就是一个  局部极小值点 。

注意：节点只有在同时存在前一个节点和后一个节点的情况下，才能成为一个 局部极大值点 / 极小值点 。

给你一个链表 head ，返回一个长度为 2 的数组 [minDistance, maxDistance] ，其中 minDistance 是任意两个不同临界点之间的最小距离，maxDistance 是任意两个不同临界点之间的最大距离。如果临界点少于两个，则返回 [-1，-1] 。

示例 1：

输入：head = [3,1]
输出：[-1,-1]
解释：链表 [3,1] 中不存在临界点。

示例 2：

输入：head = [5,3,1,2,5,1,2]
输出：[1,3]
解释：存在三个临界点：
- [5,3,1,2,5,1,2]：第三个节点是一个局部极小值点，因为 1 比 3 和 2 小。
- [5,3,1,2,5,1,2]：第五个节点是一个局部极大值点，因为 5 比 2 和 1 大。
- [5,3,1,2,5,1,2]：第六个节点是一个局部极小值点，因为 1 比 5 和 2 小。
第五个节点和第六个节点之间距离最小。minDistance = 6 - 5 = 1 。
第三个节点和第六个节点之间距离最大。maxDistance = 6 - 3 = 3 。

示例 3：

输入：head = [1,3,2,2,3,2,2,2,7]
输出：[3,3]
解释：存在两个临界点：
- [1,3,2,2,3,2,2,2,7]：第二个节点是一个局部极大值点，因为 3 比 1 和 2 大。
- [1,3,2,2,3,2,2,2,7]：第五个节点是一个局部极大值点，因为 3 比 2 和 2 大。
最小和最大距离都存在于第二个节点和第五个节点之间。
因此，minDistance 和 maxDistance 是 5 - 2 = 3 。
注意，最后一个节点不算一个局部极大值点，因为它之后就没有节点了。
示例 4：

输入：head = [2,3,3,2]
输出：[-1,-1]
解释：链表 [2,3,3,2] 中不存在临界点。

提示：

• 链表中节点的数量在范围 [2, 105] 内
• 1 <= Node.val <= 105

2.2 思路：

开始想到的是用while循环遍历做题，运行一下发现超时了。随后又换了递归的方法，不过跑起来的性能太差，但总归也能跑起来。

用栈来存储临界点的位置（索引），如果满足条件就入栈。栈中元素刚好是有序的，因为k是依次递增的。就方便了计算最小距离和最大距离。最小距离即求解相邻元素间的差值的最小值。最大距离即最后一个元素与第一个元素的差值。

递归的基准条件是last为null，此时now节点位于倒数第二个节点的位置。因为倒数第一个节点不可能成为临界点（由题）。

2.3 题解：

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    List<Integer> list = new ArrayList<>();
    int[] arr = new int[2];
    public int[] nodesBetweenCriticalPoints(ListNode head) {
        // 节点的个数少于4个的时候，临界点肯定少于两个
        if(head == null || head.next == null || head.next.next == null){
            arr[0] = arr[1] = -1;
            return arr;
        }
        recursion(head, head.next, head.next.next, 0);
        //临界点少于两个，则返回 [-1，-1] 。
        if(list.size() < 2){
            arr[0] = arr[1] = -1;
            return arr;
        }
        int min = list.get(1) - list.get(0);
        for(int i = 0; i < list.size() - 1; i++) {
            int diff = list.get(i + 1) - list.get(i);
            if(diff < min){
                min = diff;
            }
        }
        arr[0] = min;
        // 最大值肯定就是
        arr[1] = list.get(list.size() - 1) - list.get(0);
        return arr;
    }
    private void recursion(ListNode prev, ListNode now, ListNode last, int k) {
        // prev == null头节点情况
        //last == null最后一个节点情况
        // 这两种情况不可能得到极值点的
        if(prev == null || last == null){
            return;
        }
        if(now.val > prev.val && now.val > last.val || now.val < prev.val && now.val < last.val){
            list.add(k);
        }
        recursion(now, last, last.next, k+1);
    }
}