图解AVLTree

本篇文章我们将通过模拟实现AVLTree的插入来帮助大家理解AVLTree的原理。

AVLTree简单介绍    

 AVLTree即高度平衡二叉搜索树，其本质上是带了平衡功能的二叉搜索树，与普通二叉搜索树不同之处在于AVL树中任何节点的两个子树的高度最大差别为1，因为其高度平衡的特点使得其搜索的时间复杂度稳定在O(logN)。优化了普通的二叉搜索树在数据接近有序的情况下搜索的时间复杂度接近于O(N)的缺陷。

AVLTree的结点

AVLTrees的结点是由一个三叉链结构，由三个指针分别指向左子树，右子树和父节点。其数据域为pair类型。我们利用pair储存键值对，键值对（“key = value”），顾名思义，每一个键会对应一个值。pair有两个成员first,second,我们用frist储存key,second储存value。在排序时我们只关注key的大小。同时为了保证AVLTree的平衡我们引入一个概念——平衡因子。平衡因子是该节点的左子树高度与右子树高度之差。平衡因子有且仅有五个值{-2，-1，0，1，2}，当平衡因子为-2或2时代表该结点失去平衡需要调整.

//定义节点
template<class K, class V>
struct AVLTreeNode
{
	//节点的构造
    AVLTreeNode(const std::pair<K, V> kv)
		:_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
		,_kv(kv)
		,_bf(0)
	{}
	AVLTreeNode* _left;   //左子树
	AVLTreeNode* _right;  //右子树
	AVLTreeNode* _parent;//父节点 

	int _bf; //平衡因子balance factor

	std::pair<K, V> _kv; 

};

AVLTree的插入

接下来我们讨论AVLTree的插入，我们将AVLTree的插入分为三步

一，按照二叉搜素树的逻辑进行插入。

二，更新平衡因子。

三，对失衡处进行旋转处理。

1. 插入

首先我们将插入结点按照二叉搜索树逻辑进行插入。代码如下：

bool insert(const std::pair<K, V>& kv)
{
    //插入
	if (_root == nullptr)
	{
		_root = new Node(kv);
		return true;
	}
    
	Node* cur = _root;
	Node* parent = nullptr;
    //寻找结点应该在的位置
	while (cur)
	{
		if (cur->_kv.first < kv.first)
		{
			parent = cur;
			cur = cur->_right;
		}
		else if (cur->_kv.first > kv.first)
		{
			parent = cur;
			cur = cur->_left;
		}
        //树中存在相同结点插入失败
		else 
		{
			return false;
		}
	}
	cur = new Node(kv);
    //插入
	if (parent->_kv.first > kv.first)
	{
		parent->_left = cur;
		cur->_parent = parent;
	}
	else
	{
		parent->_right = cur;
		cur->_parent = parent;
	}
    //更新平衡因子
    ......
}
    

我们对该代码进行分析，首先我们处理树为空的情况，当根节点为空时该二叉树为空，此时我们将待插入结点设为根结点

if (_root == nullptr)
{
	_root = new Node(kv);
	return true;
}

接下来我们处理树不为空的情况，我们定义两个指针cur和parent。cur首先指向根节点，parent指向空。我们将待插入pair对象的frist与cur指向结点的pair的frist比较，按照二叉搜索树的规则（左子树上所有结点的值均小于它的根结点的值，右子树上所有结点的值均大于它的根结点的值）当kv.first < cur->_kv.first时，kv应该在cur的左子树上插入，当kv.first > cur->_kv.first时，kv应该在cur的右子树上插入。根据比较的结果我们让cur指向它的左子树或右子树，并用parent记录cur的父节点。循环该操作，当cur指向空时，parent就是待插入结点的父结点，接下来我们通过比较kv.frist与parent->_kv.first,确定结点的最终位置。代码如下：

Node* cur = _root;
Node* parent = nullptr;
//寻找结点应该在的位置
while (cur)
{
    if (cur->_kv.first < kv.first)
	{
		parent = cur;
		cur = cur->_right;
	}
	else if (cur->_kv.first > kv.first)
	{
		parent = cur;
		cur = cur->_left;
	}
    //树中存在相同结点插入失败
	else 
	{
		return false;
	}
}
cur = new Node(kv);
//插入
if (parent->_kv.first > kv.first)
{
	parent->_left = cur;
	cur->_parent = parent;
}
else
{
	parent->_right = cur;
	cur->_parent = parent;
}

2.更新平衡因子

现在我们对平衡因子进行更新，代码如下：

//按二叉搜索树逻辑插入
     ........
//更新平衡因子
while (parent)
{
	if (cur == parent->_left)
	{
		parent->_bf--;
	}
	else
	{
		parent->_bf++;
	}

	if (parent->_bf == 0)
	{
		break;
	}
	else if (parent->_bf == 1 || parent->_bf == -1)
	{
		cur = parent;
		parent = parent->_parent;
	}
	else if (parent->_bf == -2 || parent->_bf == 2)
	{
	    //处理失衡部分	
        ......
    }
		
}

我们对此代码进行解释，当我们在空位插入结点时只会影响根结点到插入结点路径上结点的平衡因子，其他结点的平衡因子不会改变，如图：

我们通过判断cur在parent的左子树还是右子树来对平衡因子进行修改，因为_bf=左子树高度-右子树高度；所以当cur == parent->_left时，parent->_bf--; 当cur == parent->_right时,parent->_bf++;
接下我们对parent的平衡因子，当_bf==0时，说明更新前后该结点的左右子树中的最大高度没有变化，其对祖先结点的平衡因子无影响，更新停止，跳出循环。当_bf=1/-1则说明左右子树中的最大高度改变了，应继续向上更新，于是我们让”  cur = parent;    parent = parent->_parent; “进行迭代处理。当_bf==-2/2说明该节点的左右子树高度差大于1，我们对其进行旋转处理，处理后该节点的左右子树最大高度与插入前相同，于是我们停止更新，跳出循环。

3.旋转处理

在该步骤我们将失衡状态归纳为四种：

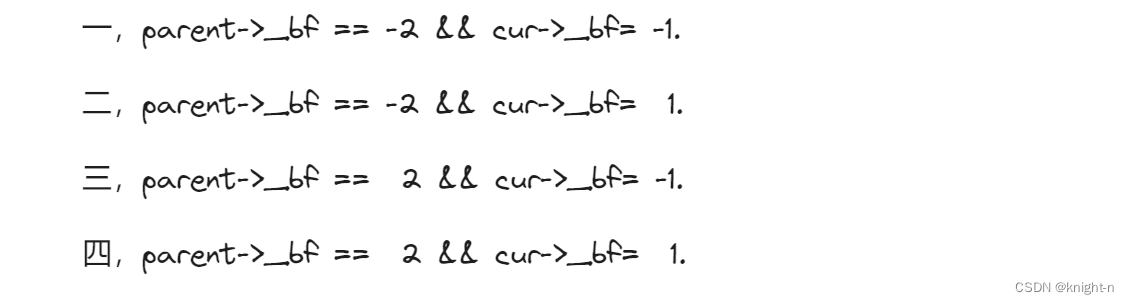
这四种情况我们分别进行左单旋处理，右单旋处理 ，左右旋处理和右左旋处理。

(1).左单旋

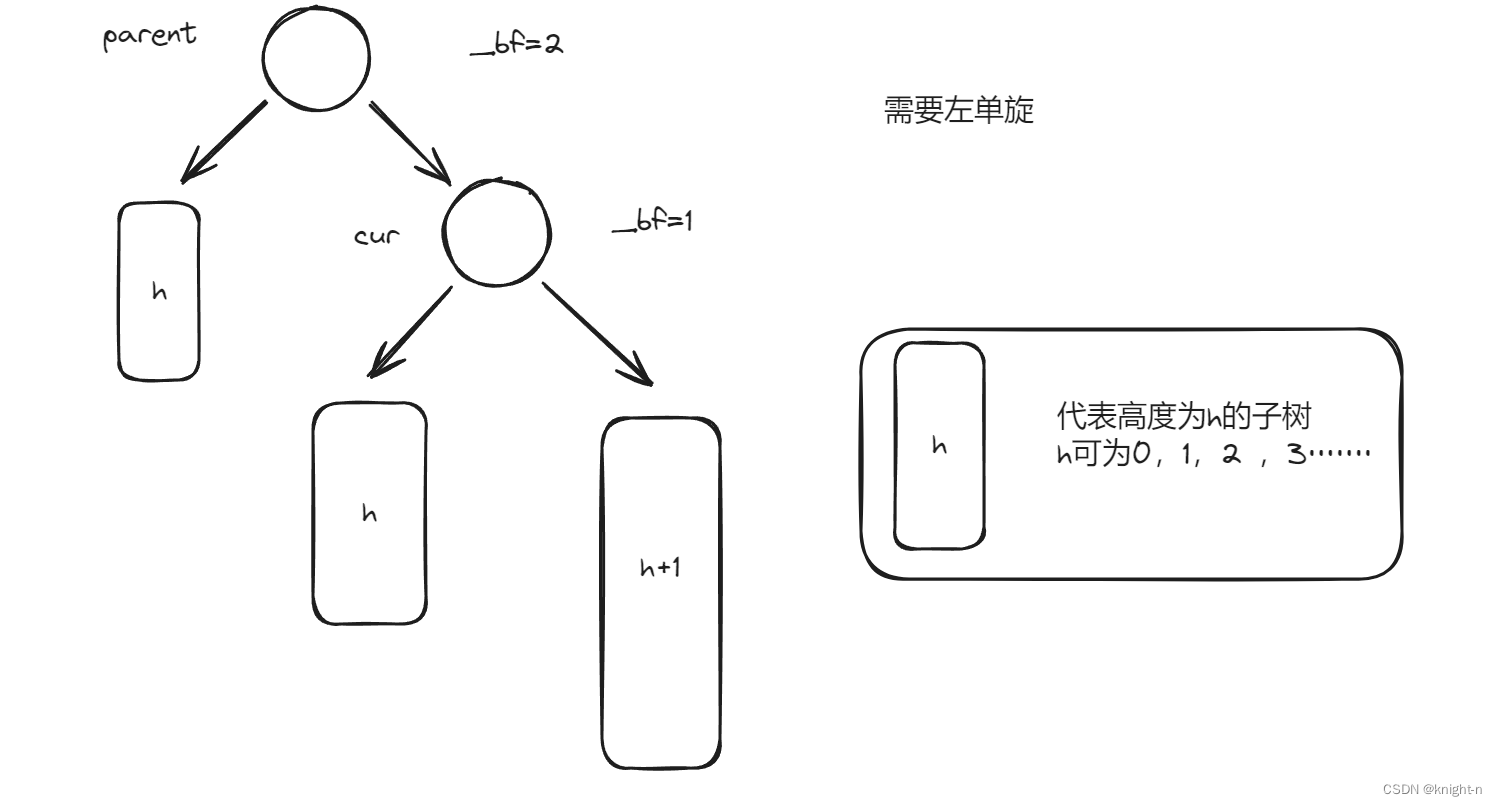
我们将所有需要左单旋的情况抽象为下图：

   

当parent的平衡因子为2，cur的平衡因子为1时，我们对其进行左旋处理。左旋分为三步：

1.让cur的左子树成为parent的右子树。

2.让parent成为cur的左子树。

3.让parent的父节点指向cur。

代码如下：

//左单旋
void RotateL(Node* parent)
{
	Node* subR = parent->_right;
	Node* ppnode = parent->_parent;
	Node* subRL = subR->_left;
	parent->_right = subRL;
	if (subRL)
	{
		subRL->_parent = parent;

	}
	subR->_left = parent;
	parent->_parent = subR;
	if (parent == _root)
	{
		_root = subR;
		subR->_parent = nullptr;
	}
	else
	{
		if (parent == ppnode->_left)
		{
			ppnode->_left = subR;
			subR->_parent = ppnode;
		}
		else
		{
			ppnode->_right = subR;
			subR->_parent = ppnode;
		}
	}
	subR->_bf = parent->_bf = 0;
}

我们让subR指向parent的右子树,用subRL指向subR的左子树，用ppnode记录parent的父节点。首先我们让parent->_right = subRL;如果subRL不为空，则让subLR的_parent指向parent。若为空则不处理，第一步完成。然后让subR的_left指向parent，让parent的_parent指向subR，第二步完成。第三步有两种情况，parent为根节点，和parent不为根结点。当parent为根节点时，让subR的_parent指向空，当parent不为根节点时，将ppnode与subR进行链接。左单旋完成后parent的_bf与subR的_bf均为0。图解：

 (2).右单旋

我们将所有需要左单旋的情况抽象为下图：

 当parent的平衡因子为-2，cur的平衡因子为-1时，我们对其进行右旋处理。右旋分为三步：

1.让cur的右子树成为parent的左子树。

2.让parent成为cur的右子树。

3.让parent的父节点指向cur。

代码如下：

//右单旋
void RotateR(Node* parent)
{
	Node* subL = parent->_left;
	Node* subLR = subL->_right;
	Node* ppnode = parent->_parent;
	parent->_left = subLR;
	if (subLR)
	{
		subLR->_parent = parent;
	}
	subL->_right = parent;
	parent->_parent = subL;
	if (parent == _root)
	{
		_root = subL;
		subL->_parent = nullptr;
	}
	else
	{
		if (parent == ppnode->_left)
		{
		    ppnode->_left = subL;
			subL->_parent = ppnode;
		}
		else
		{
			ppnode->_right = subL;
			subL->_parent = ppnode;
		}
	}
	subL->_bf = parent->_bf = 0;
		
}

其代码逻辑参考左单旋，在此不过多赘述。图解：

(3).左右双旋

我们将所有需要左右双旋的情况抽象为下图：

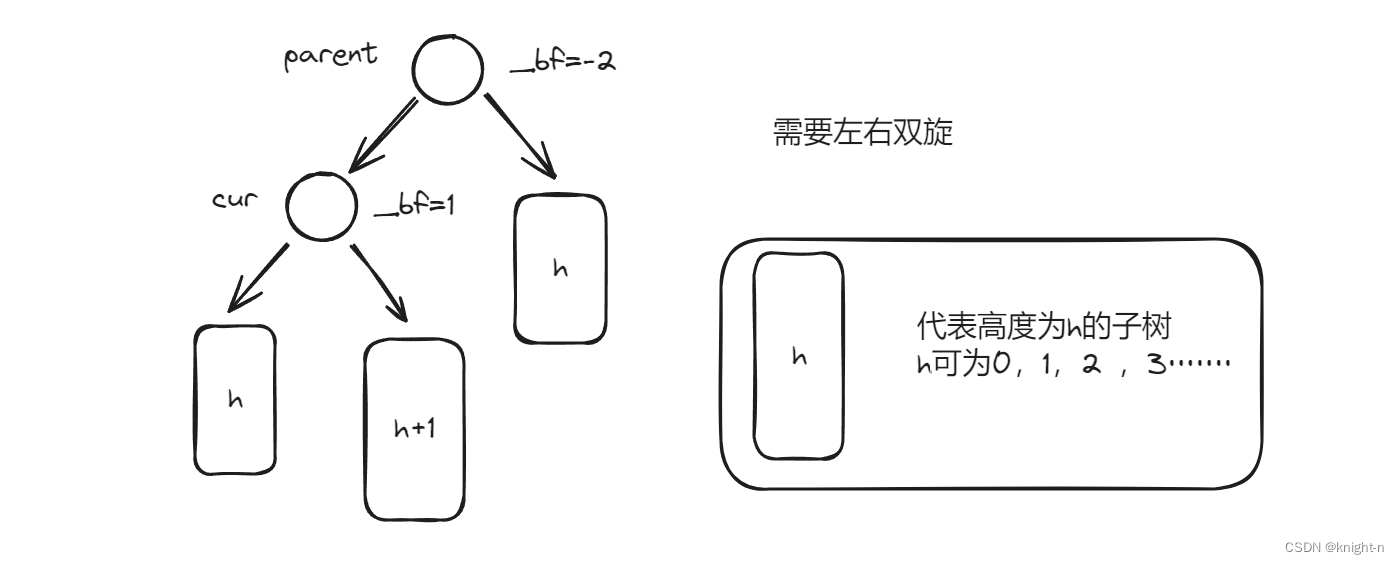
当parent的平衡因子为-2，cur的平衡因子为1时，我们对其进行左右双旋处理。左右双旋分三步：

一，对cur进行左旋。

二，对parent进行右旋。

三，更新平衡因子。

代码如下：

//左右双旋
void RotateLR(Node* parent)
{
	Node* subL = parent->_left;
	Node* subLR = subL->_right;
	int bf = subLR->_bf;
	RotateL(subL);
	RotateR(parent);
	if (bf == 1)
	{
		subL->_bf = -1;
	}
	else if (bf == -1)
	{
		parent->_bf = 1;
	}

}

前两步我们不过多介绍，我们着重介绍第三步。更新平衡因子时有三种情况。一，subLR->_bf=1.

二，subLR->_bf=-1。三，subLR的平衡因子为0即subLR为新插入结点。这三种情况下更新后的subL的和parent的平衡因子不同。参考下图：

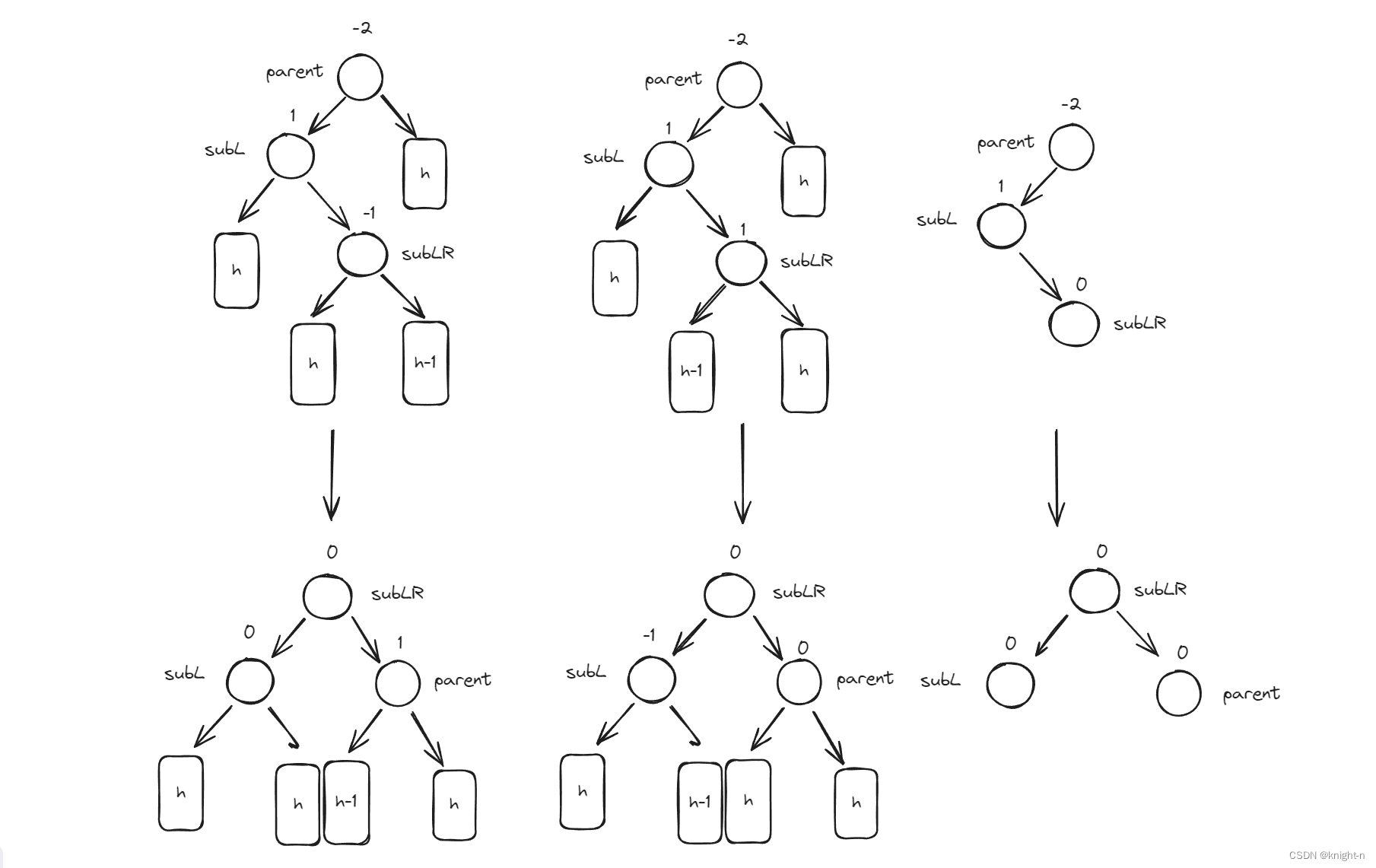
 (4).右左双旋

我们将所有需要右左双旋的情况抽象为下图：

当parent的平衡因子为2，cur的平衡因子为-1时，我们对其进行右左双旋处理。右左双旋分三步：

一，对cur进行右旋。

二，对parent进行左旋。

三，更新平衡因子。

代码如下：

//右左双旋
void RotateRL(Node* parent)
{
	Node* subR = parent->_right;
	Node* subRL = subR->_left;
	int bf = subRL->_bf;
	RotateR(subR);
	RotateL(parent);
	if (bf == -1)
	{
		subR->_bf = 1;
	}
	else if (bf == 1)
	{
		parent->_bf = -1;
	}
}

代码逻辑同左右双旋。

小结

我们对所有代码进行整合：

bool insert(const std::pair<K, V>& kv)
{
			if (_root == nullptr)
			{
				_root = new Node(kv);
				return true;
			}

			Node* cur = _root;
			Node* parent = nullptr;
			while (cur)
			{
				if (cur->_kv.first < kv.first)
				{
					parent = cur;
					cur = cur->_right;
				}
				else if (cur->_kv.first > kv.first)
				{
					parent = cur;
					cur = cur->_left;
				}
				else
				{
					return false;
				}
			}
			cur = new Node(kv);
			if (parent->_kv.first > kv.first)
			{
				parent->_left = cur;
				cur->_parent = parent;
			}
			else
			{
				parent->_right = cur;
				cur->_parent = parent;
			}
			
			while (parent)
			{
				if (cur == parent->_left)
				{
					parent->_bf--;
				}
				else
				{
					parent->_bf++;
				}

				if (parent->_bf == 0)
				{
					break;
				}
				else if (parent->_bf == 1 || parent->_bf == -1)
				{
					cur = parent;
					parent = parent->_parent;
				}
				else if (parent->_bf == -2 || parent->_bf == 2)
				{
					if (parent->_bf == 2)
					{
						if (cur->_bf == 1)
						{
							RotateL(parent);
						}
						else  if (cur->_bf == -1)
						{
							RotateLR(parent);
						}
					}
					if (parent->_bf == -2)
					{
						if (cur->_bf == 1)
						{
							RotateR(parent);
						}
						else if(cur->_bf == -1)
						{
							RotateRL(parent);

						}
					}
					break;
				}
				
			}

			return true;
}

总结

以上是我们对AVLTree插入的讲解，感谢您的观看！！！！