高斯光束大气传播特性的仿真与测量设计

一、高斯光束的理论公式

1. 光强分布

高斯光束在横截面上的光强分布为：

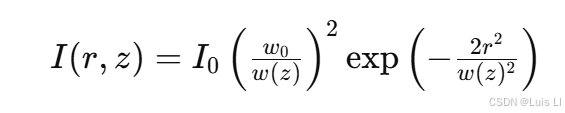
其中：

• I0：束腰处的最大光强。
• r：离光轴的径向距离。
• w(z)：在距离 zzz 处的光斑半径。
• w0​：束腰处的最小光斑半径。

1. 光斑半径变化

光斑半径随传播距离的变化为：

其中，瑞利长度 Zr定义为：

λ为光的波长。

1. 相位分布

高斯光束的相位分布为：

其中：

• k=2π/λ​：波数。
• ：波前曲率半径。

---

二、大气衰减的朗伯定律

当光束在大气中传播时，光强按照朗伯定律呈指数衰减：

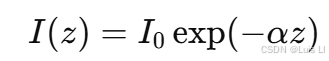
其中：

• α：大气衰减系数。
• I0​：入射光强。
• z：传播距离。

---

三、模型的建立与线性化

1. 综合模型

结合高斯光束的传播特性和大气衰减，得到光强随距离的综合模型：

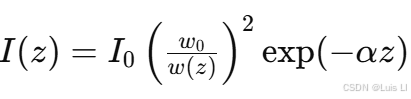
1. 模型线性化

为了使用最小二乘法，需要将模型线性化。取自然对数：

如果在束腰附近，，则：

这样，模型变为关于 z的线性关系。

---

四、最小二乘法拟合

1. 数据准备

• 测量：在不同距离 zi处测量光强 Ii​。
• 线性化：

1. 建立线性方程

1. 计算最小二乘解

目标是最小化残差平方和：

% 参数设定
w0 = 1e-3; % 光束束腰半径 (m)
lambda = 6.328e-9; % 波长 (m)
zR = pi * w0^2 / lambda; % 瑞利长度 (m)
alpha_true = 0.01; % 大气衰减系数 (1/m)
I0 = 1; % 入射光强

% 生成距离数据
z = linspace(0, 50, 100); % 传播距离 (m)

% 计算光斑半径
w_z = w0 * sqrt(1 + (z / zR).^2);

% 计算接收光强
I_z = I0 * (w0 ./ w_z).^2 .* exp(-alpha_true * z);

% 加入测量噪声
noise_level = 0.05; % 噪声水平
I_z_noisy = I_z .* (1 + noise_level * randn(size(I_z)));

% 数据线性化
y = log(I_z_noisy);

% 最小二乘法拟合
p = polyfit(z, y, 1);
alpha_fit = -p(1);
ln_I0_fit = p(2);

% 绘制结果
figure;
scatter(z, y, 'b', 'DisplayName', '测量数据');
hold on;
plot(z, polyval(p, z), 'r-', 'DisplayName', '线性拟合');
xlabel('传播距离 z (m)');
ylabel('ln(I)');
title('大气衰减的最小二乘法拟合');
legend;
grid on;

% 显示拟合结果
fprintf('真实大气衰减系数 alpha = %.4f 1/m\n', alpha_true);
fprintf('拟合大气衰减系数 alpha = %.4f 1/m\n', alpha_fit);
fprintf('相对误差 = %.2f%%\n', abs((alpha_fit - alpha_true) / alpha_true * 100));

六、结果分析

• 拟合精度：通过比较拟合得到的α 和真实值，可以评估拟合的准确性。
• 误差来源：噪声、模型近似（忽略 w(z）的变化）都会影响结果。
• 改进方法：若发现误差较大，可考虑非线性拟合，或者在模型中保留w(z) 的变化。

---

七、注意事项

1. 模型精确性：当传播距离较大时，不能忽略w(z) 对光强的影响，需使用非线性拟合方法。

2. 数据质量：实验数据的准确性直接影响拟合结果，需确保光功率计和测距仪的精度。

3. 环境因素：大气参数可能随环境变化（如湿度、温度），在实验中应尽量控制或记录这些因素。

4. Matlab仿真：代码中参数可根据实际情况调整，注意单位一致性。

---

八、总结

通过结合高斯光束的传播特性和大气衰减的朗伯定律，我们建立了光强随传播距离变化的数学模型。利用最小二乘法对模拟数据进行了拟合，成功估计了大气衰减系数。该仿真过程不仅验证了理论模型，也为实际实验的数据处理和分析提供了参考。

MWORK代码（清除注释%，更换为#，注意单双引号）

% 参数设定
w0 = 1e-3; % 光束束腰半径 (m)
lambda = 532e-9; % 波长 (m)
zR = pi * w0^2 / lambda; % 瑞利长度 (m)
alpha_true = 0.01; % 大气衰减系数 (1/m)
I0 = 1; % 入射光强

% 生成距离数据
z = linspace(0, 50, 100); % 传播距离 (m)

% 计算光斑半径
w_z = w0 * sqrt(1 + (z / zR).^2);

% 计算接收光强
I_z = I0 * (w0 ./ w_z).^2 .* exp(-alpha_true * z);

% 加入测量噪声
noise_level = 0.05; % 噪声水平
I_z_noisy = I_z .* (1 + noise_level * randn(size(I_z)));

% 数据线性化
y = log(I_z_noisy);

% 最小二乘法拟合
p = polyfit(z, y, 1);
alpha_fit = -p(1);
ln_I0_fit = p(2);

% 绘制结果
figure;
scatter(z, y, 'b', 'DisplayName', '测量数据');
hold on;
plot(z, polyval(p, z), 'r-', 'DisplayName', '线性拟合');
xlabel('传播距离 z (m)');
ylabel('ln(I)');
title('大气衰减的最小二乘法拟合');
legend('show');
grid on;

% 显示拟合结果
fprintf('真实大气衰减系数 alpha = %.4f 1/m\n', alpha_true);
fprintf('拟合大气衰减系数 alpha = %.4f 1/m\n', alpha_fit);
fprintf('相对误差 = %.2f%%\n', abs((alpha_fit - alpha_true) / alpha_true * 100));