动态规划入门之线性递推DP（爬梯类问题）

原创

于 2024-11-13 20:20:29 发布 · 952 阅读

17 ·

CC 4.0 BY-SA版权

文章标签：

#动态规划 #算法

动态规划整体上模板性不强，甚至很隐晦。因此我写了这个专题，从动态规划入门到废弃。我所使用的题单一部分是灵茶山艾府的，一部分是平时刷题遇到的。这里我是对解题思路的一些细节补充，便于理解。如果觉得我的补充比较啰嗦，可以去看灵茶山艾府的原版解题。

这一类入门的动态规划，其实本质上是高中的排列组合+递推数列（甚至高中生会比很多大学生有更清晰的思路。）包括我们最熟悉的斐波那契数列，也是一个递推数列。广义上来说，所有于递推有关的，都属于动态规划。

为了方便阅读我将题目都copy下来了（包括中英文题目和测试样例）

70. 爬楼梯

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？
示例 1：
输入： n = 2
输出： 2
解释： 有两种方法可以爬到楼顶。

1 阶 + 1 阶
2 阶
示例 2：
输入： n = 3
输出： 3
解释： 有三种方法可以爬到楼顶。
1 阶 + 1 阶 + 1 阶
1 阶 + 2 阶
2 阶 + 1 阶
提示：

1 <= n <= 45

Analysis

在这里插入图片描述

这其实是一道高中排列组合之数列递推问题。
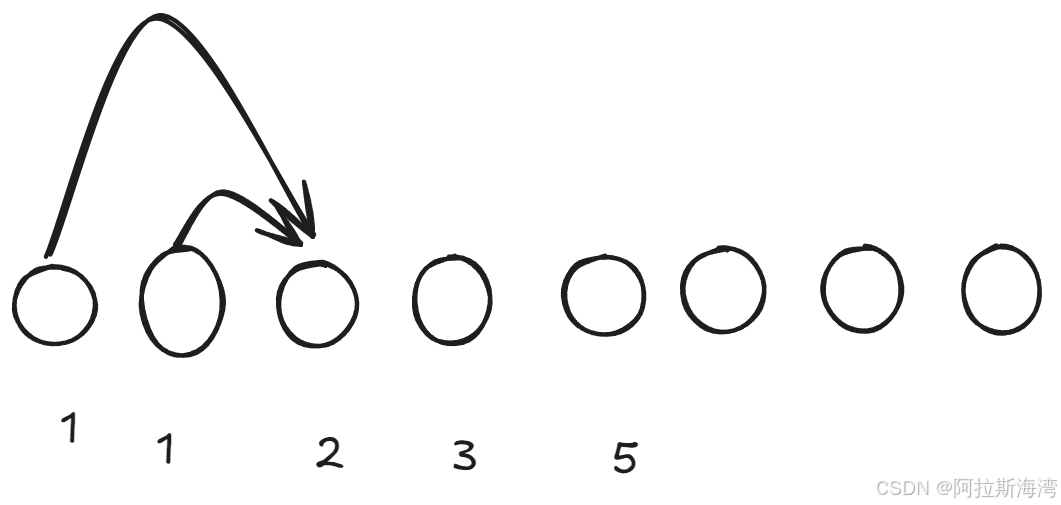
要想爬上第i个楼梯，只有两条路径：

爬到第i-2个楼梯，再爬两格
爬到第i-1个楼梯，再爬一格。
设 $a_{i}$ 为爬到第i个楼梯的方案数。则 $a_{i} = a_{i-1} + a_{i-2}$ 。

Solution

from functools import cache  
  
class Solution:  
    @cache  
    # 记忆化递归  
    def fibonacci_cache(self, n: int) -> int:  
        if n == 0:  
            return 0  
        elif n == 1 or n == 2:  
            return 1  
        else:  
            return self.fibonacci(n-1) + self.fibonacci(n-2)  
    # 非递归，迭代  
    def fibonacci(self, n: int) -> int:  
        a, b = 1, 1  
        for i in range(2, n+1):  
            a, b = b, a+b  
        return a  
    def climbStairs(self, n: int) -> int:  
        return self.fibonacci_cache(n+1)  
        # return self.fibonacci(n+1)  
  
if __name__ == '__main__':  
    s = Solution()  
    print(s.climbStairs(1))

#include <iostream>  
#include <cstring>  
  
using namespace std;  
  
class Solution {
   
     
private:  
    int *cache;  
public:  
    int climbStairs(int n) {
   
     
        cache = new int [n+1];  
        memset(cache, 0, sizeof(int ) * (n+1));  
        int rst =  this->fibonacci_cache(n+1);  
        delete []cache;  
        return rst;  
    }  
  
    int fibonacci_cache(int x) {
   
     
        if (x == 1 or x == 2) return 1