计算机组成原理知识点汇总（五）计算机运算方法

原创已于 2025-06-03 20:36:06 修改

· 817 阅读

14 ·

版权

文章标签：

#计算机组成原理 #计算机组成 #硬件架构

于 2025-06-03 20:35:34 首次发布

计算机组成原理专栏收录该内容

6 篇文章

订阅专栏

一、无符号数和有符号数

（1）概念

无符号数：只能表示非负数值。假如一个 8 位的无符号整数，其取值范围是从 0（二进制 0000 0000）到 255（二进制 1111 1111）

有符号数：能表示正、负和零。为了表示符号，计算机通常会用二进制的最高位作为符号位，0 代表正数，1 代表负数。其余位表示数值大小。例如 8 位有符号整数，取值范围是 -128 到 127 。常见的表示方法有原码、反码和补码。

（2）有符号数详解

机器数：将符号数字化的数，如将负号变为1，将正号变为0，如10001表示-1

真值：带+、-的值，如+100

表示方法有如下三种：

原码表示法

用最高位表示符号（0 为正，1 为负），剩余位表示数值的绝对值。

整数符号位与数值位用逗号分隔，如：0，1110表示+1110

小数符号位与数值位用点号分割，如：1.1110表示-0.1110

设机器字长为 n 位，真值为 X，则：

正数原码：符号位为 0，数值部分为 X 的二进制表示。
负数原码：符号位为 1，数值部分为 |X| 的二进制表示。

注意，0 的原码有两种表示：+0 = 00000000，-0 = 10000000

优点：直观易懂，与真值转换简单。
缺点：
1. 符号位需单独处理，加减运算复杂（需判断符号和绝对值大小）。
2. 0 的表示不唯一，浪费编码空间。

补码表示法

通过引入 “模运算” 将负数转换为正数，从而将减法运算转化为加法运算，解决原码加减的缺陷。

设机器字长为 n 位，真值为 X，则：

正数补码：与原码相同，符号位为 0，数值部分不变。
负数补码：符号位为 1，数值部分为原码数值位取反（按位非）后加 1（末位加 1）。

例（8 位补码）：

十进制5 = 00000101
十进制-5：原码 10000101 → 取反 11111010 → 加 1 得11111011
0 的补码唯一：00000000 不存在-0

优点：
1. 符号位参与运算，加减运算统一为加法（无需判断符号）。
2. 0 的表示唯一，编码空间利用率高。
3. 可表示范围更大：n 位补码范围为-2^{n-1}到 2^{n-1}-1（如 8 位补码为-128到+127）。
缺点：真值与补码的转换需计算（负数需取反加 1）。

补充：

补码有一位符号数和两位符号数

其中两位符号数补码，又叫变形补码

在双符号位补码中，数值的符号由两个符号位表示：

第一个符号位：表示数值的实际符号，0表示正数，1表示负数。
第二个符号位：作为数值的一部分，随着数值的移位而变化。

例如：

正数：00xxxxxx
负数：11xxxxxx

移码表示法

主要用于表示浮点数的阶码（指数部分），通过给真值加上一个固定偏移量，使编码后的数值全为正数，便于快速比较大小。

简单来说，就是-1001和-1003不好比较大小，所以都给他们加1000，就成了-1和-3比大小

现在，对于移码表示法来说，就是都加2的n次方

即，设机器字长为 n 位，真值为 X，则移码为：移码 = X + 2^{n-1}

例（8 位移码，偏移量2的7次方，即128 ）：

+5十进制 = 5 + 128 = 133十进制 = 10000101
-5十进制 = -5 + 128 = 123十进制 = 01111011
0 的移码：0 + 128 = 128十进制= 10000000（唯一表示）。

优点：
1. 编码后的二进制数大小直接反映真值大小（无需考虑符号，可直接按无符号数比较）。
2. 0 的表示唯一，且移码与补码数值部分相同（符号位相反）。
缺点：仅用于特定场景（如浮点数阶码），不用于一般数值运算。
应用：IEEE 754 浮点数标准中阶码的表示（8 位移码偏移量为 127，需注意与上述定义的偏移量差异）。

二、数的定点表示和浮点表示

（1）定点表示

定点数分为定点整数和定点小数。

所谓定点表示，简单来说，就是小数点按约定方式给出·的数。

约定方式有以下两种：

对于定点整数来说，小数点按约定放在最后

对于定点小数来说，小数点按约定放在符号位后

（2）浮点表示

浮点表示：把数的范围和精度分别表示的方法，相当于数的小数点位置随比例因子的不同而在一定的范围内可以自由浮动。

机器浮点数由以下部分组成：

尾数（符号为M）：以定点小数形式存储，决定数值的精度（有效位数越多，精度越高）。例如，尾数位数越多，能表示的细节越精细。
阶码（指数，符号为e）：以定点整数形式存储，决定数值的范围（指数越大，数值范围越广）。例如，阶码位数越多，可表示的数值范围越大。
符号位：
- 数符：表示整个浮点数的正负（如0为正，1为负）。
- 阶符：单独表示指数的正负。

举个例子：

假设其结构为：1位阶符 + 3位阶码（指数） + 1位数符 + 4位尾数，总长度共9位。

现在我们用浮点数来表示十进制数 -5.5

十进制数 5.5 的二进制形式为 101.1

将二进制数 101.1 转换为科学计数法形式（规格化）：

得到：

尾数（M）：0.1011（小数点后4位，即纯小数部分）。
指数（e）：3（即小数点需右移3位）。

然后再确定符号位：

数符：因数值为负数，数符位为1。
阶符：指数为正3，阶符位为0（假设阶符0表示正，1表示负）。

然后确定编码阶码和尾数：

阶码（3位）：指数值3的二进制为 11，补足3位为 011。
尾数（4位）：取规格化后的纯小数部分 1011（即小数点后的4位）。

最后组合各部分，得到：

（3）IEEE 754标准

早期不同厂商（如IBM、DEC、Cray等）的浮点数格式互不兼容，所以有了IEEE 754标准

制定如下常用三个标准格式：

32位浮点数的标准格式

64浮点数的标准格式

80浮点数的标准格式

另外，要知道

在 IEEE 754 浮点数标准中，阶码是用移码表示的（移码的定义：移码 = 真值 + 偏移值）

原因：移码将所有指数转换为无符号数，使得阶码的二进制值可以直接按大小排序，无需考虑符号。且通过偏置值，将实际指数 E，平移到无符号数范围。从而支持正负指数的统一表示。

所以要知道，将浮点数的指数真值e变成阶码E时，应将指数e加上一个固定的偏移值

偏移值计算公式如下：

对于 n 位的阶码，偏置值为：

单精度（32位浮点数）：阶码占 8 位 →127。
双精度（64位浮点数）：阶码占 11 位 → 1023。

三、定点运算

（1）移位运算

意义：当某计算机没有乘除法运算线路时，可借助移位和加法结合，实现乘除运算

规则如下：

对于有符号数（算术移位）

左移1位：机器数对应真值的绝对值变为原来2倍

右移1位：机器数对应真值的绝对值变为原来1/2倍

关于空位填谁，规则如下：

对于正数：移位时空位填0
对于负数：
是原码时移位后空位填0
是补码左移时空位填0，右移时空位填1
是反码时移位后空位填0

对于无符号数（逻辑移位）

无符号数只有正数

无符号数的移位时，不区分正负，移位时空位都填充为0，无论是左移还是右移。

（2）加法与减法运算

在计算机内部，数值通常是以补码形式存储的，所以这里采用补码加减法。

补充知识点：mod运算

模运算（mod） 是一个数学运算，它表示一个数除以另一个数后所得到的余数。

例如，7mod 3=17mod3=1，因为7除以3商为2，余数为1。

1.补码加法

整数加法：

对于两个整数 A和 B，它们的补码表示分别为 A补和 B补，加法的公式为：

简单解释来说，就是：直接将两个补码相加，得到的结果也就是 A+B的补码，而如果其进位超出范围，进位就会被丢弃。

比如A=0.1011 B=-0.0101

A补 +B补=10.0110

产生了进位1，直接丢掉就好

所以最后结果为0.0110

小数加法：

处理小数时，实际操作也类似于整数加法，直接对补码加法进行操作，最后将溢出部分抛掉。

2.补码减法

整数减法：

补码减法实际上是通过将被减数转为其补码后加上减数的补码来完成的，所以

对于两个整数 A 和 B，其补码表示分别为 A补和 B补，减法的公式为：

同样最后将溢出部分抛掉

小数减法：

减法的公式为：

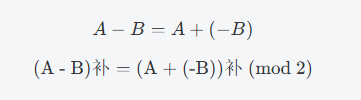
同样最后将溢出部分抛掉

（3）溢出判断

溢出指的是在进行加法、减法等运算时，结果超出了计算机用来表示数值的位数范围。即如果运算结果的数值部分侵占了符号位的位置，从而导致符号位发生改变或者产生不符合预期的结果 ，就发生了溢出。

比如两个负数的二进制X和Y：

X：-10010

Y：-10101

二者转换成补码后，相加得1 010001

位数多了一位，机器上最后只显示010001

所以两个负数相加，最后得到了正数？？？

肯定不对，这就是因为前面得那个1溢出了。

数有一位符号数和两位符号数，判断如下：

对于一位符号的数们来说：

对于，谁可能会溢出，现在有定论：

对于加法，只有正数加正数、负数加负数两种情况下可能溢出

对于负数，只有正数减负数，负数减正数两种情况下可能溢出

总结一下，有如下定论：

无论加法还是减法，只要参加运算的两个数符号相同，结果又与原那两个数符号不同，即为溢出。

对于两位符号数们来说：

2位符号的补码，即变形补码。

有如下定论：

当2位符号位不同时，则溢出，否则，无溢出。且无论是否溢出，最高位符号位永远代表真正的符号。

几个例子：

A= - 0.1000 B= - 0.1000 求【A+B】补

A补=1.1000 B补=1.1000

【A+B】补=1 1.0000

红1多出来了，直接丢掉，最终为1.0000 结果符号同原操作数符号，故无溢出。

（注：前面多出来的这个“1”并不代表溢出，因为最终结果是正确的，关于溢出定义见上文有写）

设x= - 11/16 y= - 7/16 计算x+y

x= - 0.1011 y= - 0.0111

x补=11.0101 y补=11.1001

x补+y补=1 10.1110

红1多出来了，直接丢掉，最终为10.1110 符号为10，故溢出

（注：如果溢出，最前面符号为1则是负溢出，最前面符号为0则是正溢出）

补充：

两个正数相加，结果大于机器所能表示的最大正数，称为上溢。
两个负数相加，结果小于机器所能表示的最小负数，称为下溢。

（4）乘法运算

计算机中没有乘法，其本质是加法和移位两种运算共同作用的结果。

原因：比如计算0.1101x0.1011

在手动计算中，其就是先算加法，然后移一位，以此类推的计算。计算机效仿此过程

计算机中的乘法：

原码一位乘法规则

乘积符号由两原码符号位异或结果
乘积数值由两数绝对值相乘

知道了这个规则，就可以进行计算，那么对于计算机内部是怎样进行的呢？

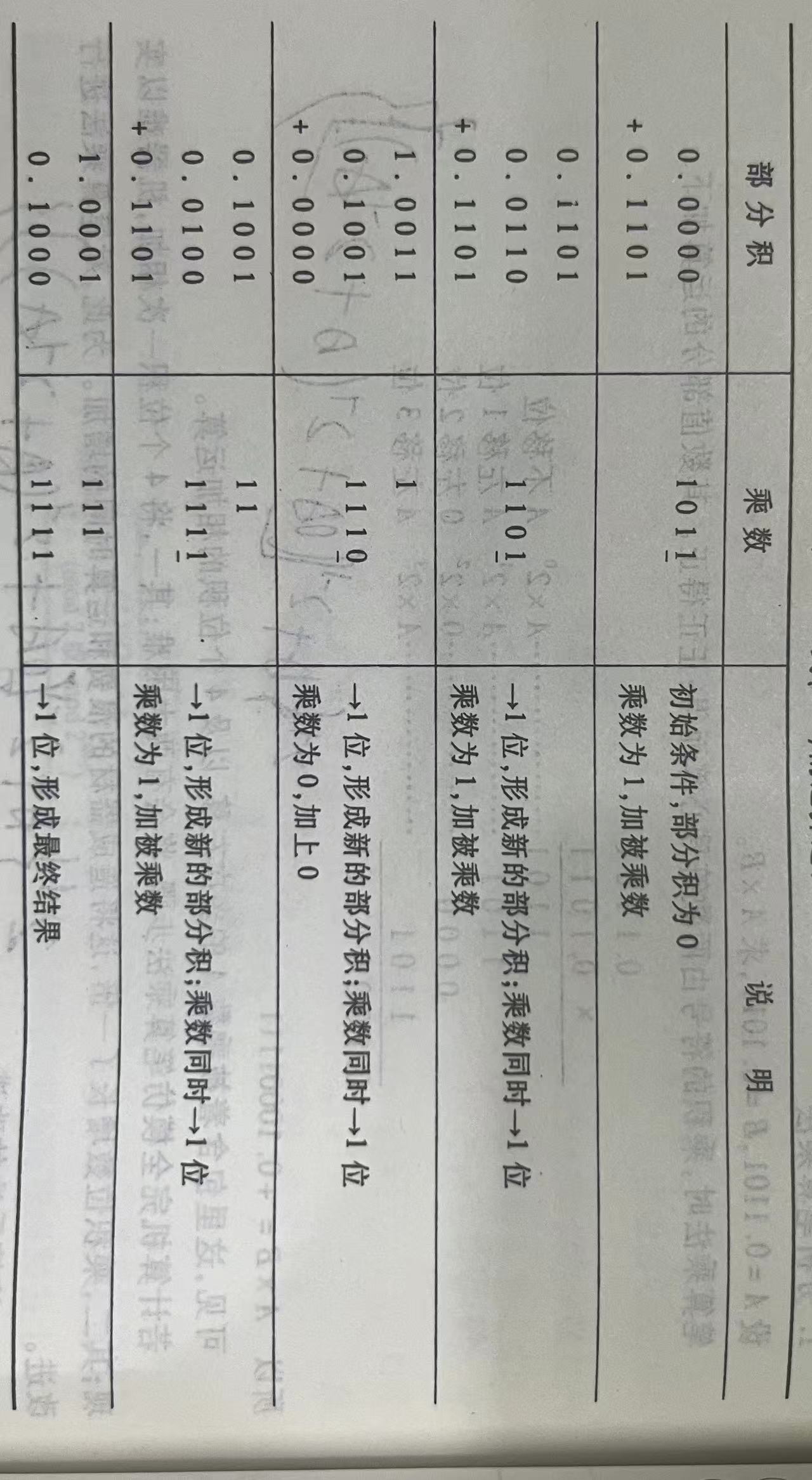
比如

A=0.1101 B=0.1011 两数相乘

书上是这么写的：

详细解释：

原值： A=0.1101 B=0.1011

符号位： A为0 B为0

数值位： A为1101 B为1011

计算符号位：0异或0=0

计算数值位：（重在看懂图表）

第一行：

最开始，我们要从0开始往上加，就是初始值0.0000 （对应蓝圈）

把A数值位拿过来与B的最低位相乘，B是1011，最低位是1 （对应红圈）

得到0.1101x1=0.1101，放到初始值下面，准备与初始值相加（对应绿圈）

第二行：

与初始值相加后，得到：0.1101写到第二行部分积部分（对应蓝圈）

此时整行数为：0.1101 1011（1011在第一行）（对应绿圈）

将其整体右移一位，多的数扔掉，空的位置用0补齐

得到新数：0.01101101 （对应红圈）

将此时乘数部分（1101）的最低位乘原A的数值位

得到数：0.1101，准备与得到的新数相加（对应黑圈）

第三行

相加得到的数位1.0011 （对应蓝圈）

此时整行数为：1.0011 1101 （对应绿圈）

将其整体右移一位，多的数扔掉，空的位置用0补齐

得到新数：0.10011110 （对应红圈）

将此时乘数部分（1110）的最低位乘原A的数值位

得到数：0.0000，准备与得到的新数相加（对应黑圈）

第四行同理

第五行：

最终得到数：1.0001                           （对应蓝圈）

此时整行数为：1.0001 1111                           （对应绿圈）

将其整体右移一位，多的数扔掉，空的位置用0补齐

得到新数：0.1000 1111    （对应红圈）

此时新数的右半部分1111是初始值0000再经过运算后

向右移了四位得到的，至此左半部分数，全移到了右边，可以结束了。

得到最终数0.1000 1111

注：乘法运算依靠移位和加法实现，两个4位数相乘，需要进行4次加法和4次移位

所以最终结果为：0.1000 1111

明白以上过程，再看书中总结的东西，就懂了：

原码两位乘法（了解即可）

原码两位乘法与原码一位乘法一样，符号位运算和数值位分开进行

规则也大差不差，都是依靠移位和加法实现，过程也同原码一位乘法一样

唯几点不同如下：

在原码一位乘法中，我们是乘数的最低位乘A数值位，然后右移一位

在原码两位乘法中，要加某倍数的原部分积，再移两位

在原码一位乘法中，移位后最高位一直是补0

在原码两位乘法中，还要看乘数的最低两位（乘数判断位），和部分积的最高位（标志位）

将其总结成下图，原码两位乘法规则：

举例如下：

x=0.111111 y= - 0.111001 求x*y

符号位： x为0 y为1

数值位： x为111111 y为111001

然后我们在最前面补上两位0（为了将符号位和数值位分开处理，不懂记住就可）

得到： x为00111111 y为00111001

然后部分积记得加上标志位，初始值为0

所以此时第一行完整数为 000. 000000 00111001

于是有如下运算过程：

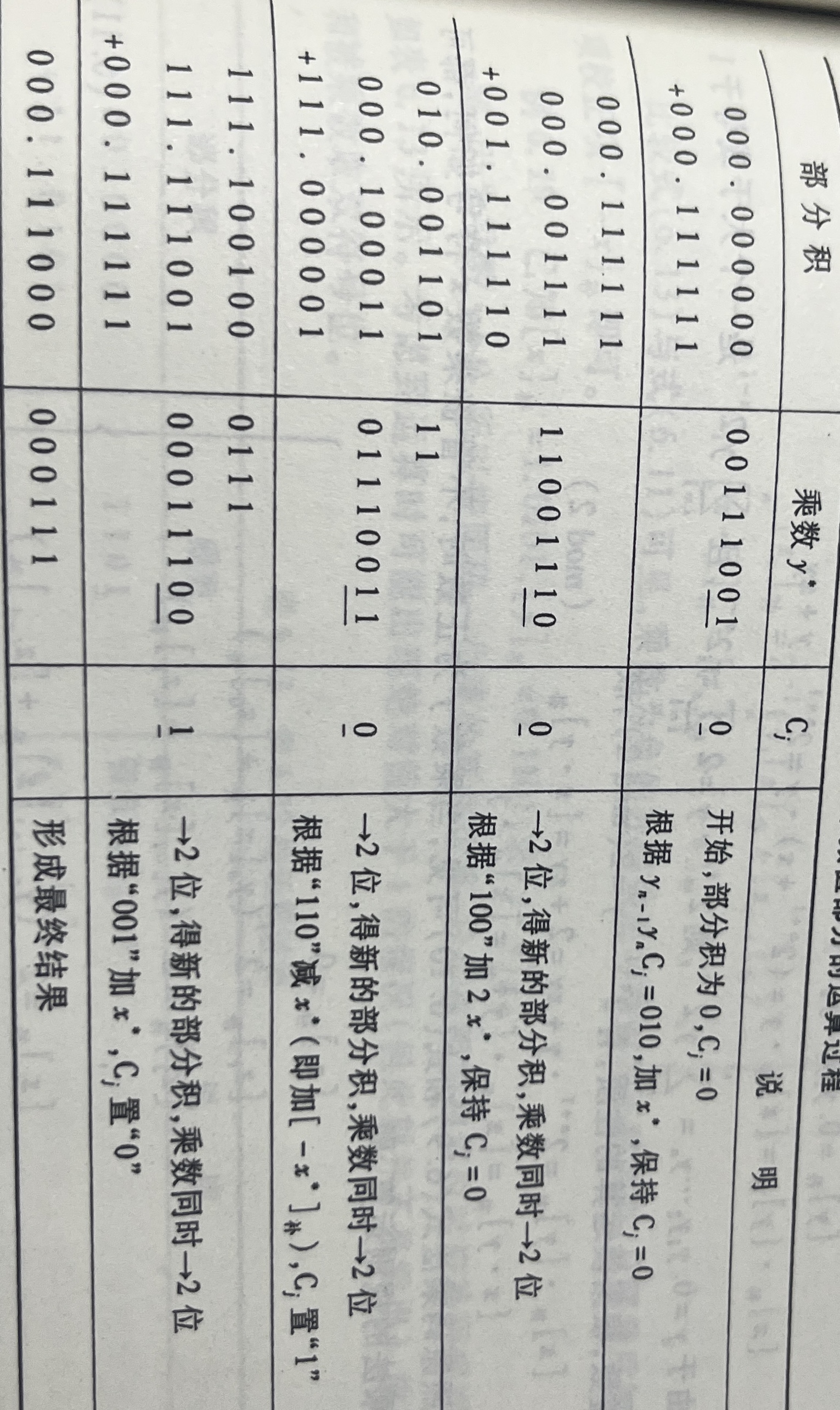
第一行

最低两位01，最高位0——所以部分积加|x|，然后右移两位，补0

得到第二行数：000.001111 11001110

第二行

最低两位10，最高位0——所以部分积加2|x|，右移两位，补0

得到第三行数：000.100011 01110011

第三行

最低两位11，最高位0——所以部分积加3|x|，右移两位，补1

得到第四行数：111.111001 00011100

第四行

最低两位00，最高位1——所以部分积加|x|，右移两位，补0 （溢出数扔掉）

得到第五行数：000.111000 000111

至于到底移位几次？

答：对乘数的位数 n 除以 2 后向上取整。

计算符号位：

0异或1得到1

所以最终结果为1.111000 000111

补码一位乘法

补码一位乘法分为两种：校正法和Booth算法

校正法

如果y>0，那么计算过程同原码一位过程一样
如果y<0，那么只需按照原码一位规则计算后，再加上-x补即为最终结果

举个例子

x补=1.0101 y补0.1101 求[x·y]补

此时乘数y>0，所以按照计算过程同原码一位过程一样：

唯一一点，这里取双符号位（考虑运算时出现绝对值大于1情况）

所以此时x补=11.0101

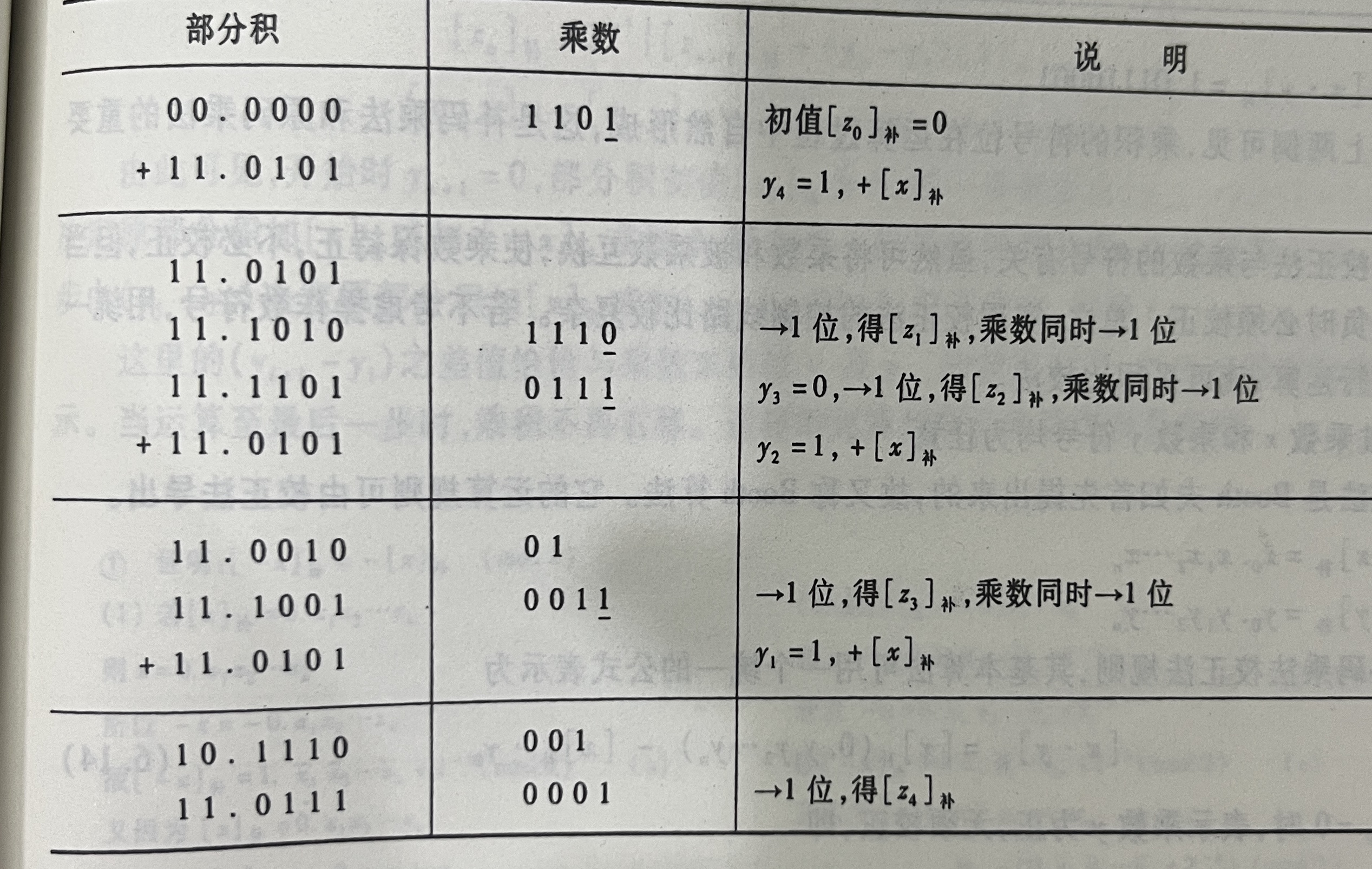
第一行

初始值00.0000 乘数1101

所以直接+x补后，向右移一位

得到第二行数11.1010 1110 （注：符号位保持不变还是11，详细说明在后面）

第二行

乘数最低位为0，所以加0后，直接右移一位

得到下面的数：11.1101 0111

乘数最低位为1，所以加x补后，直接右移一位

得到第三行数：11.1001 0011

第三行、第四行同理，最后即可得出最终结果

（注：关于移位，一般都是数值位有几位，就移位几次，此次数值位4位，所以总共移位4次后即可结束）

关于符号位在移位时不变的说明：

比如

数：00.0101 它向右移位时直接补0即可
数：11.0101 它向右移位时，要保持符号位不变，所以无论移几位，开头都是11。比如移1位，它应该变成11.1010；移2位，它应该变成11.1101。即，相当于开头要补1。
数10.1101 它向右移位时，要保持符号位不变，跟上面一样，相当于开头要补1。所以，移1位之后，它应该变成11.0110

总结一下，开头到底补什么？

最高位是什么就补什么
是1补1，是0补0

Booth 算法

遵循规则如下：

首先在乘数最低位后填一个附加位0
移位时，符号位保持不变
然后遵循以下规则即可

另外：

在整个运算过程中依据乘数末位和附加位进行(n + 1)步操作（n为乘数数值位位数），最后一步不移位，得到的部分积即为最终结果，无需对附加位做额外处理来得到乘积的补码。

举个例子：

x补=0.1101 y补0.1011 求[x·y]补

因为x补=00.1101 所以-x补=11.1101

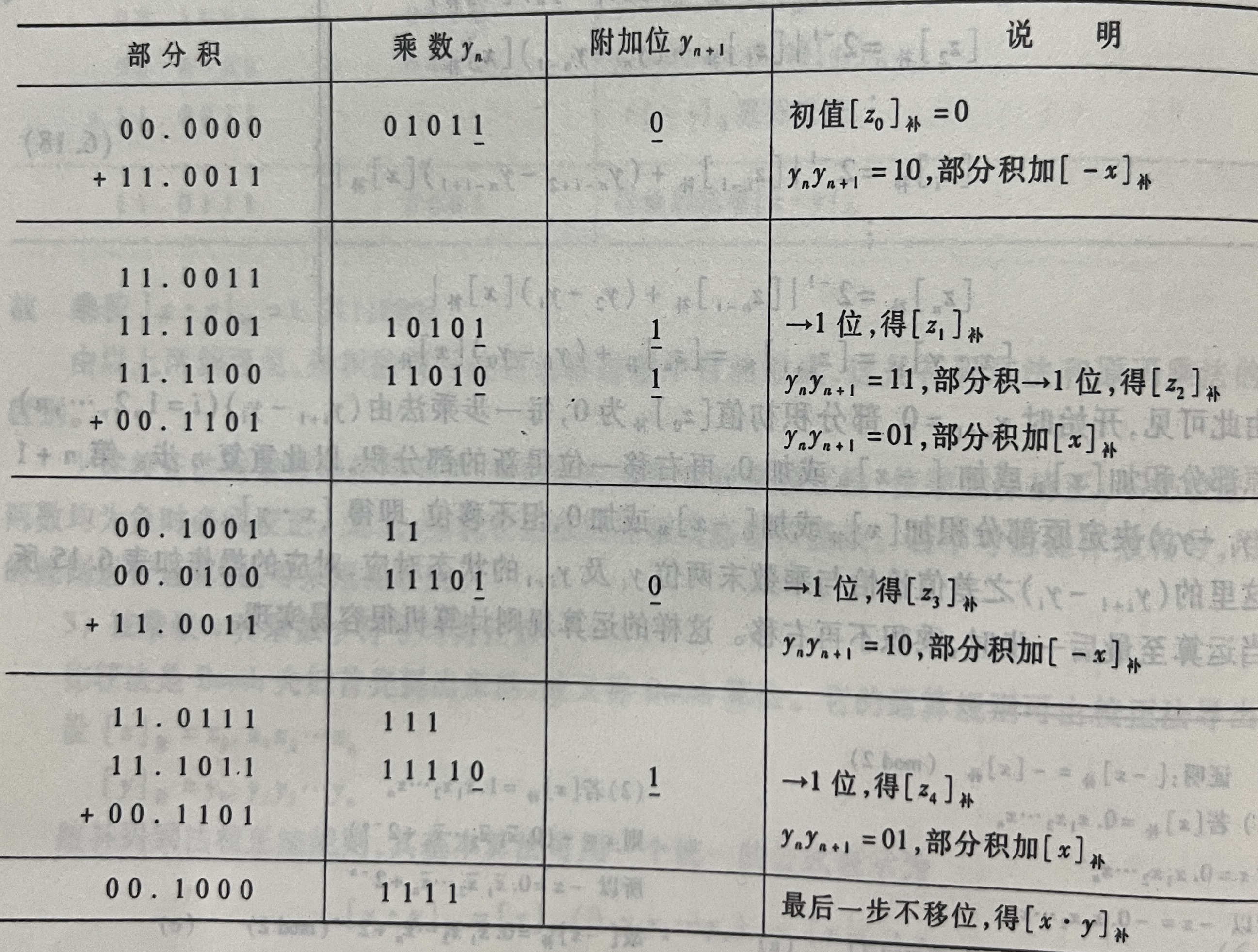
第一行

初始值00.0000 乘数01011 附加位0

所以进行操作：部分积加-x补，右移一位

得到第二行数：11.1001 10101 1 （符号位11不变）

第二行

数：11.1001 10101 1 乘数最低位1 附加位1

所以进行操作：部分积右移一位

得到数：11.1100 11010 1

此时乘数最低位0 附加位1

所以进行操作：部分积加x补，右移一位

得到第三行数：00.0100 11101 0

第三行

数：00.0100 11101 0 乘数最低位1 附加位0

所以进行操作：部分积加-x补，右移一位

得到第四行数：11.1011 1110 1

第四行

数：11.1011 1110 1 乘数最低位0 附加位1

所以进行操作：部分积加x补，右移一位

但由于是最后一步，所以不进行移位

得到第五行数：00.1000 1111

所以最终结果为：0.1000 1111

（5）除法运算

原码除法

原码除法也分两种：恢复余数法和不恢复余数法

同样遵循规则：

商的符号位单独处理x与y异或运算
数值部分为绝对值相除|x|/| y|

恢复余数法

具体规则：

x补+ [-y*]补后

当余数>0时（可上商1），将该数左移一位后，加 [- y]*补
当余数<0时（可上商0），将该数加上y*补，左移一位，加 [- y]*补
最终结果，即为依次上商组成的数

余数，即最高位

y*，即y的数值位

举个例子：

x= - 0.1011 y= - 0.1101 求[x/y]原

x原=1.1011 x*=0.1011

y原=1.1101 y*=0.1101 y*补=0.1101 [-y*]补=1.0011

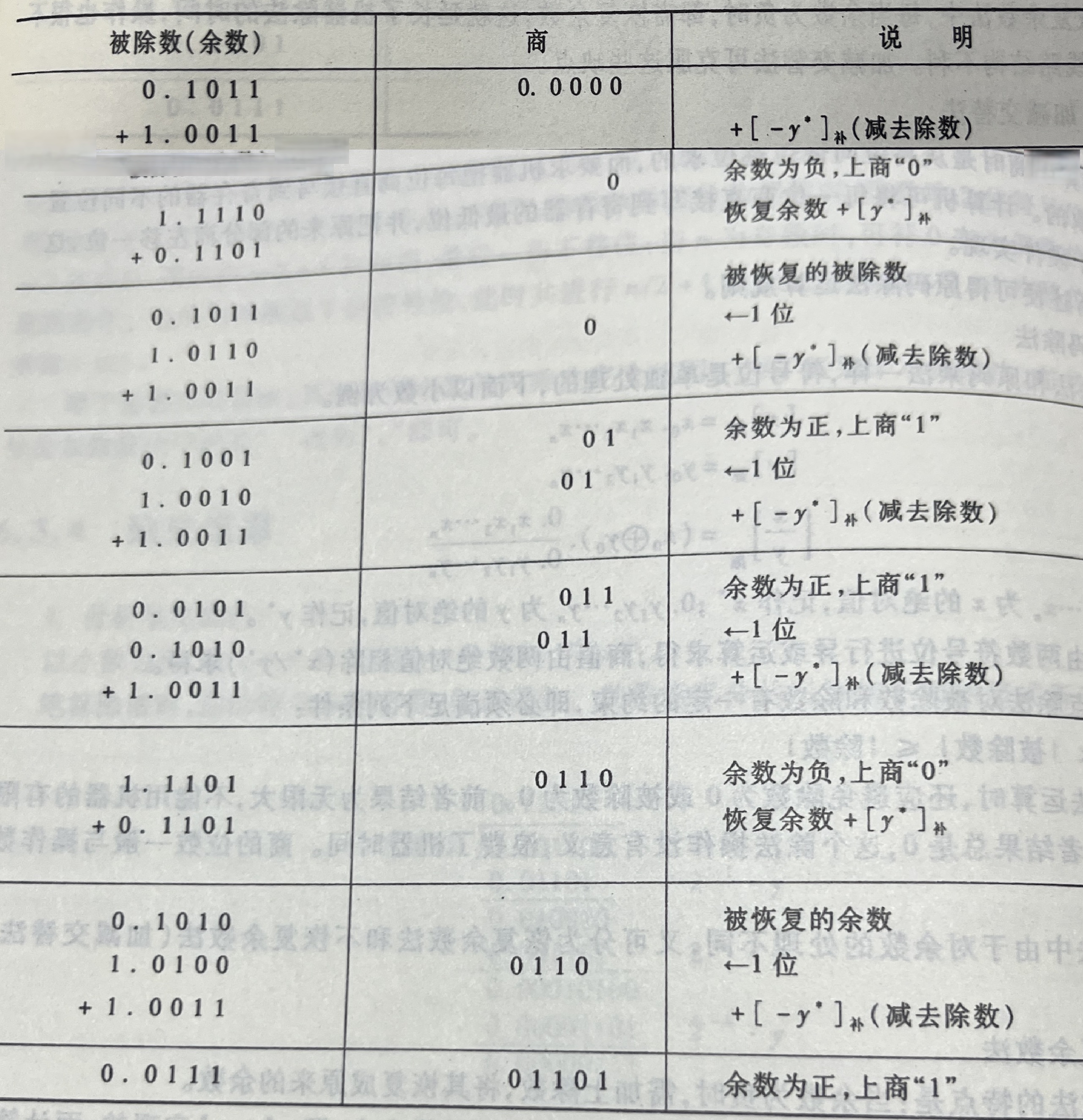
第一行

x补+ [-y*]补

得到第二行数：1.1110

第二行

数：1.1110 余数（最高位）为1，所以是负 上商0

所以进行操作：将该数加上y*补，左移一位，加 [- y]*补

得到第四行数：0.1001

第四行

数：0.1001 余数>0 上商1

所以进行操作：将该数左移一位后，加 [- y]*补

得到第五行数：0.0101

第五行

数：0.0101 余数>0 上商1

所以进行操作：将该数左移一位后，加 [- y]*补

得到第六行数：1.1101

第六行

数：1.1101 余数（最高位）为1，所以是负 上商0

所以进行操作：将该数加上y*补，左移一位，加 [- y]*补

得到第八行数：0.0111

第八行

数：0.0111 余数>0 上商1

此时商位=xy的位数，结束

数值位最终结果为商位组成的数：01101

符号位=1异或1=0

所以最终结果为0.1101

不恢复余数法（加减交替法）

具体规则：

x补+ [-y*]补后

结果为负，直接左移加[y*]补
结果为正，加[-y*]补

举个例子：

x= - 0.1011 y=0.1101 求[x/y]原

x原=1.1011 x*=0.1011

y原=0.1101 y*=0.1101 y*补=0.1101 [-y*]补=1.0011

如果看懂了恢复余数法的例子，再看这个例子应该就很好懂了

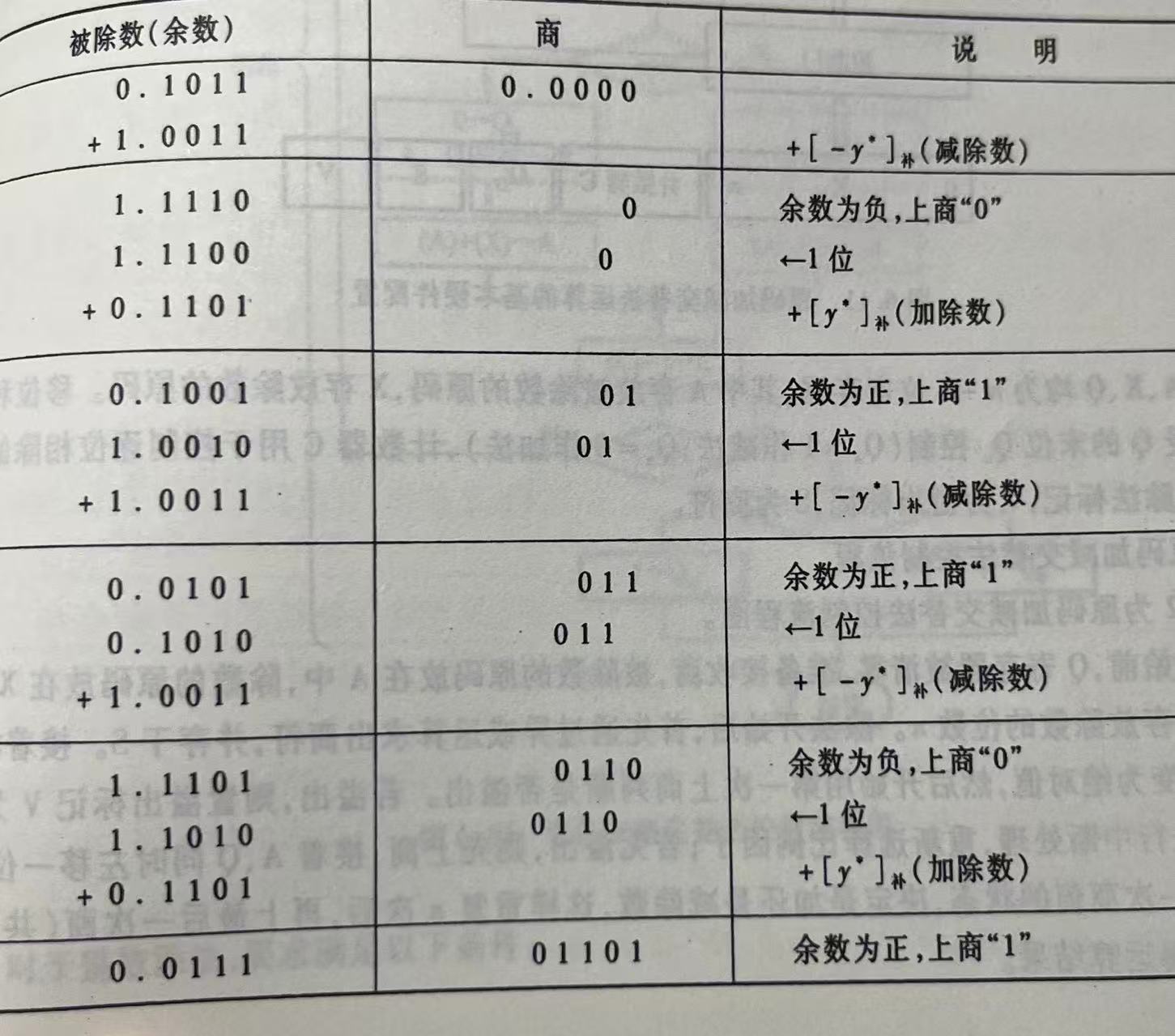
商位依次为01101

符号位计算：1异或0=1

所以最终结果为：1.1101

四、浮点运算

（1）加减运算

对于两个浮点数，其计算名称及步骤如下：

对阶：让两个小数点对齐
尾数求和：将两个小数的尾数按定点运算加减规则求和（求差）
规格化：增加有效数字位数，提高精度
舍入：为提高精度，考虑尾数右移时丢失的数值位
溢出判断：判断结果是否溢出

举个例子：

两浮点数：和分别为x和y，计算x+y=？

对于x，已经是规格化形式，阶码Ex=01，尾数Mx = 0.1101

对于y，已经是规格化形式，阶码Ey = 11，尾数My=- 0.1010

按步骤：

第一步：对阶

求阶差ΔE=Ey−Ex=11 - 01 = 10 （这里是二进制减法）

二进制10即为十进制2，所以须将x的尾数右移2位，即阶码加2

x右移后，阶码Ex'=01 + 10=11 Mx′=0.001101 （右移时，高位补0）

第二步：尾数求和

因为计算机中用补码进行加法运算

所以事先求得：[Mx']补=0.001101 My补=1.0110

所以[Mx']补+[My]补=0.001101 + 1.0110=1.100101

第三步：规格化处理

得到的结果1.100101是非规格化形式，所以需进行规格化调整

（注：何为规格化数，后文详细说明）

这里采用左规

左移 1 位：尾数变为 1.001001（符号位不变，低位补 0），

阶码减 1：从 11变为 10

左规后结果： 1.001001

第四步：舍入（0舍1入法）

数值位有6位，超过精度值4位，故需舍弃最低两位01

舍弃的最低两位的最高位为0，所以直接舍弃即可

（注：舍入规则，后文详细说明）

第五步：溢出判断

指数为10，在 2 位指数范围内（00 到 11，对应十进制 0 到 3），所以无溢出。

（注：溢出规则，后文详细说明）

最终结果为1.0010

转化为原码=1.1110

故

附录：何为规格化数？

在补码表示下，规格化尾数的形式为：

对于正数，是0.1xx……
对于负数，是1.0xx……

主要是开头一个必须是0.1一个必须是1.0，原因如下：

比如，若不进行规格化，都表示同一个数，但形式不唯一。而规格化后，统一写成0.1xx……这种形式，消除了这种不唯一性。

如果不是这样的形式，就需要进行规格化处理

处理方法如下：

左规

定义：当浮点数运算结果的尾数出现特定形式，如在补码表示下为00.0××××（正数）或11.1××××（负数）时，需要进行左规操作。操作方式是将尾数左移一位，同时阶码减1 。
举例：若得到的尾数为00.0101，左移一位变为00.1010，阶码减1 。可能需多次左规，直到尾数符合规格化要求。

右规

定义：当浮点数运算结果的尾数出现溢出情况，即补码表示下为01.××××（正数）或10.××××（负数）时，要进行右规。操作是将尾数右移一位，同时阶码加1 。
举例：若尾数运算结果为01.0101，右移一位变为00.10101，阶码加1 ，右规一般只需进行一次。

舍入规则

两种常用方法

0舍1入法（类似二进制"四舍五入"）

规则：

若被舍去部分的最高位为0 → 直接截断（舍去）。
若被舍去部分的最高位为1 → 向最低有效位进位（+1）

示例（4位尾数，舍入第5位及以后）：
- 0.1101 | 0xx... → 舍去后 0.1101（最高位为0）
- 0.1101 | 1xx... → 进位 0.1110（最高位为1）

恒置1法

规则：
- 无论舍去部分的值如何，强制将结果的最低有效位设为1

示例（4位尾数）：
- 0.1100 | xxx... → 置1 → 0.1101
- 0.1101 | xxx... → 置1 → 0.1101（不变）

溢出判断

上溢

下溢

无溢出

2位指数系统中，若 E=0,1,2（移码01~11）均有效。

五、ALU电路

（1）什么是ALU

ALU即算术逻辑单元，简称ALU，是计算机里负责运算的组件。

在 CPU 中负责执行算术运算（如加减乘除）和逻辑运算（如与、或、非、异或）的核心部件。

它长这个样：

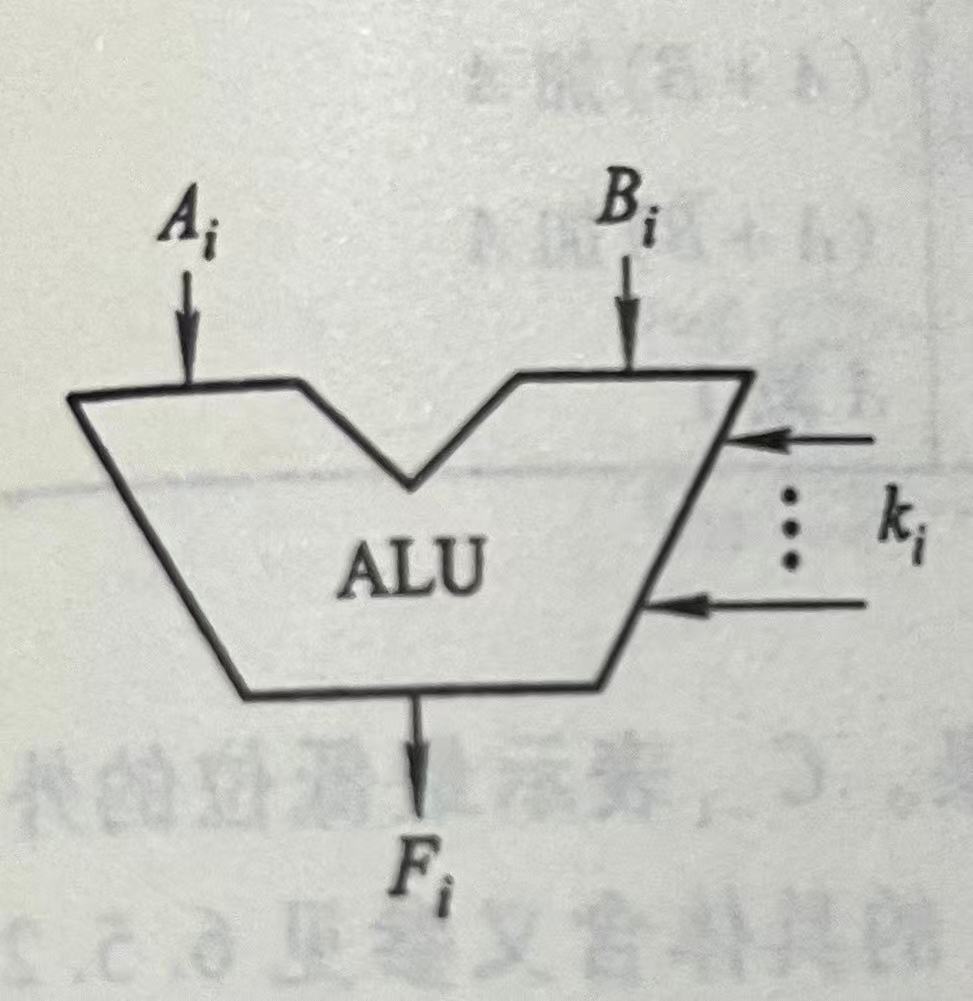
A和B为输入端口

K为控制信号

F为输出端口

ALU的加法、减法、乘法、除法都是需要加法器完成的，因此为了提高加法器的速度，最好的办法就是所有位数能够并行运算，而高位两个数加法需要加上低位的进位，所以现在的问题就是如何快速计算出每一位的进位出来

这就用到了下方的知识：

（2）快速进位链

前言：并行加法器

并行加法器是指所有位的加法运算同时进行的电路，由多个全加器并行连接而成。

根据加法器的不同结构，有了两种截然不同的进位信号处理方式：串行进位链和并行进位链

串行进位链

核心原理

逐位依赖：每一位的进位信号必须等待前一位的进位计算完成后才能产生，像多米诺骨牌一样依次传递。
硬件实现：由多个全加器串联组成，每位全加器的进位输出连接到下一位的进位输入。

典型特点

优点：
- 电路结构简单，仅需串联全加器，硬件成本极低。
- 设计复杂度低，适合小规模电路。
缺点：
- 速度极慢：进位延迟随位数呈线性增长。例如，32 位加法器的进位需从第 1 位逐位传到第 32 位，每级全加器产生约 1 个门延迟，总延迟为 32 个门延迟。
- 位数越多，延迟越显著，无法满足高速计算需求。

应用场景

低速、低功耗场景：如简单嵌入式系统、低速外设接口、教学用计算器。
位数极少的场景：如 4 位加法器（早期计算机或实验电路）。

并行进位链

核心原理

并行计算所有进位：通过数学推导，将进位信号分解为进位生成信号（G）和进位传播信号（P），直接用原始输入信号（Ai, Bi）和初始进位C-1计算出所有位的进位，无需逐位等待。
- 进位生成信号（G）：，表示当前位无需低位进位即可产生进位
- 进位传播信号（P）：，表示当前位可将低位进位传递到高位
- 所有进位信号可通过逻辑门并行计算，仅需 \(O(1)\) 级门延迟（与位数无关）。

典型特点

优点：
- 速度极快：进位延迟固定，不随位数增加而显著增长。
- 适合高速计算场景，如 CPU 的算术逻辑单元（ALU）。
缺点：
- 硬件复杂度极高：需额外逻辑门计算所有 Gi, Pi和各级进位表达式，逻辑门数量随位数呈指数增长（需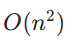个门）。
- 位数较多时（如 64 位），电路规模庞大，功耗较高。