关于带权并查集的总结-CSDN博客

本文链接：https://blog.csdn.net/2301_81888203/article/details/140896569

~~~加油！~~~

先由一道经典题说起：

问题 B: 【并查集】食物链II

时间限制: 1.000 Sec 内存限制: 128 MB

题目描述

动物王国中有三类动物A,B,C，这三类动物的食物链构成了有趣的环形。A吃B， B吃C，C吃A。
现有N个动物，以1－N编号。每个动物都是A,B,C中的一种，但是我们并不知道它到底是哪一种。
有人用两种说法对这N个动物所构成的食物链关系进行描述：
第一种说法是"1 X Y"，表示X和Y是同类。
第二种说法是"2 X Y"，表示X吃Y。
此人对N个动物，用上述两种说法，一句接一句地说出K句话，这K句话有的是真的，有的是假的。当一句话满足下列三条之一时，这句话就是假话，否则就是真话。
1）当前的话与前面的某些真的话冲突，就是假话；
2）当前的话中X或Y比N大，就是假话；
3）当前的话表示X吃X，就是假话。
你的任务是根据给定的N（1 <= N <= 50,000）和K句话（0 <= K <= 100,000），输出假话的总数。

输入

第一行是两个整数N和K，以一个空格分隔。
以下K行每行是三个正整数 D，X，Y，两数之间用一个空格隔开，其中D表示说法的种类。
若D=1，则表示X和Y是同类。
若D=2，则表示X吃Y。

输出

只有一个整数，表示假话的数目。

样例输入

样例输出

那么，这种类型题，我一开始想到它可能和并查集有关，不过由于这是带指向的，所以我们不能停留在普通的并查集，即“属于一个集合”。这时，这道题就可以用带权值的并查集来算。（当然还有一种方法叫 种类并查集）

不过，我觉得光想着两个东西的权值加加减减很难理解，所以我会用距离来理解权值。设置一个数组d[N]，来表示每个节点到跟节点的距离。那么，如果a->b，就不难理解d[a]-d[b]=1；不过，以防万一这个式子左边可能是负的，我们写代码时要多加一些处理，即取模。

（顺带一提取模这个东西。今天才发现它很神奇。比如一个100位的数a（当然给的是字符串），要求a%b，我们可以取a的每一位...~~算了写下来吧~~。

string a;
int n;//要求a%n的值
int t=0;
for(auto i:a){
    t=(t*10+i-'0')%n;//感觉余数是有点“传递性”的
}
cout<<t<<endl;

扯远了...不过余数这部分我还很蒙www，渴望有大佬来指点...跪谢）

那么，根据“距离”这个概念，我们可以轻易得出，da=db:同类；da-db=1:a吃b；db-da=1:b吃a；

思路为：1.判断a，b是否已经在一个集合

2.若不在一个集合，合并，并更新d[fa_a]的值（d[fa_b]也ok）

3.若在一个集合，判断即可

所以，这个并查集与普通并查集不同的区别大概有：1.find要更新d

2.unit的方式有多种

下面就看看代码吧：

#include<iostream>
using namespace std;
int n,k,s,x,y;
int fa[1000010],d[1000010];
int find(int i){
	if(fa[i]==i){
		return i;
	}
	int t=fa[i];
	fa[i]=find(fa[i]);
	d[i]=((d[i]+d[t])%3+3)%3;
	return fa[i];
}
int main()
{
	cin>>n>>k;
	for(int i=1;i<=n;i++){
		fa[i]=i;
	}
	int ans=0;
	while(k--){
		cin>>s>>x>>y;
		if(x>n||y>n){
			ans++;
			continue;
		}
		if(s==2&&x==y){
			ans++;
			continue;
		}
		int fa_x=find(x),fa_y=find(y);
		if(s==1){
			if(fa_x==fa_y){
				if((d[x]-d[y]+3)%3!=0){
					ans++;
				}
			}else{
				fa[fa_x]=fa_y;
				d[fa_x]=(d[y]-d[x]+3)%3;
			}
		}else{
			if(fa_x==fa_y){
				if((d[x]-d[y]+3)%3!=1){
					ans++;
				}
			}else{
				fa[fa_x]=fa_y;
				d[fa_x]=(d[y]-d[x]+4)%3;
			}
		}
//		cout<<ans<<endl;
	}
	cout<<ans;
	return 0;
}

综上所述，感觉带权值的并查集主要应用方面为：给出的多个物件成“环”，或有明确指向关系。

题型可以为判断加入的关系是否正确。

补充：现在再补充一道可以用带权值的并查集来做的：

五行学说的基本观点如下：
。。。（删掉了，废话）
下图可以更快地理解相生相克的关系：

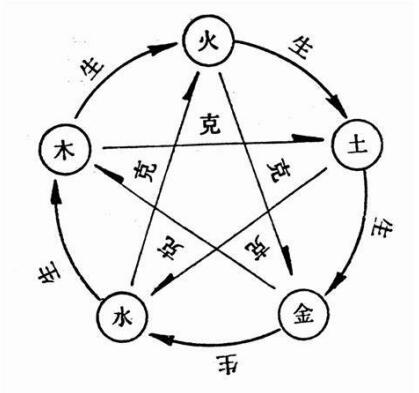
小爱的身边有的 n 个物品，每个物品都应该具有五行中的一种属性。小爱对这些物品进行了 m 次观察，每次观察都是会发现两种物质之间的相生或相克关系。但这些观察不一定可靠，如果本次观察与之前的记录没有矛盾，则将这条观察记录下来；否则，直接忽视该条观察。
请你帮助小爱统计一下，有多少条观察是被忽略的。

输入

第一行：两个整数表示 n 和 m；
第二行到第 m 行：每行表示一条观察，首先有一个字符，然后有两个整数参数 x 和 y：

+ 相生关系以字母 `s` 开头，表示 x 生 y；
+ 相克关系以字母 `k` 开头，表示 x 克 y；

输出

单个整数：表示输入中出现矛盾的记录条数。

样例输入

样例输出

提示

+ 对于 30% 的数据，1≤n,m≤10；
+ 对于 60% 的数据，1≤n,m≤103；
+ 对于 100% 的数据，1≤n,m≤105。

那么，一开始可能会疑惑，这是两个环，难道要设计两个环的并查集来单独做吗？但又会发现，这两个环又是有一定的关系的。所以这时候的带权并查集就要加入一点巧思：相克的两者d只差若为1，相生的两者d只差就为2。所以还是只要用一个环来维护就好，只不过d的表达可能要略微改变。

代码：

#include<iostream>
using namespace std;
//const int N=1000010;
int n,m,fa[1000010],d[1000010];
char s;
int x,y;
int find(int i){
    if(fa[i]==i){
        return fa[i];
    }
    int t=fa[i];
    d[i]=(d[i]+d[t])%5;
    fa[i]=find(fa[i]);
    return fa[i];
}
int main()
{
    cin>>n>>m;
    int ans=0;
    for(int i=1;i<=n;i++){
        fa[i]=i;
    }
    while(m--){
        cin>>s>>x>>y;
        int fa_x=find(x),fa_y=find(y);
        if(s=='s'){
            if(fa_x==fa_y){
                if((d[x]-d[y]+5)%5!=1){
                    ans++;
                }
            }else{
                fa[fa_x]=fa_y;
                d[fa_x]=(d[y]-d[x]+1+5)%5;
            }
        }else{
            if(fa_x==fa_y){
                if((d[x]-d[y]+5)%5!=2){
                    ans++;
                }
            }else{
                fa[fa_x]=fa_y;
                d[fa_x]=(d[y]-d[x]+2+5)%5; 
            }
        }
    }
    cout<<ans;
    return 0;
}

注意，这里关于距离，都要保证是正的，所以都要有先加再取模的操作。