统计方形（数据加强版）

题目描述：统计方形（数据加强版）

有一个 n m 方格的棋盘，求其方格包含多少正方形、长方形（不包含正方形）。

输入格式：

一行，两个正整数 n,m（n <= 5000,m <= 5000）。

 输出格式：

一行，两个正整数，分别表示方格包含多少正方形、长方形（不包含正方形）。

 样例输入 1
2 3

样例输出 1
8 10

解题思路：

矩形数=正方形数+长方形数

矩形数的计算公式（长为m，宽为n）：（1+2+3+....+n）*(1+2+3+....+m)

上面公式的推导过程：

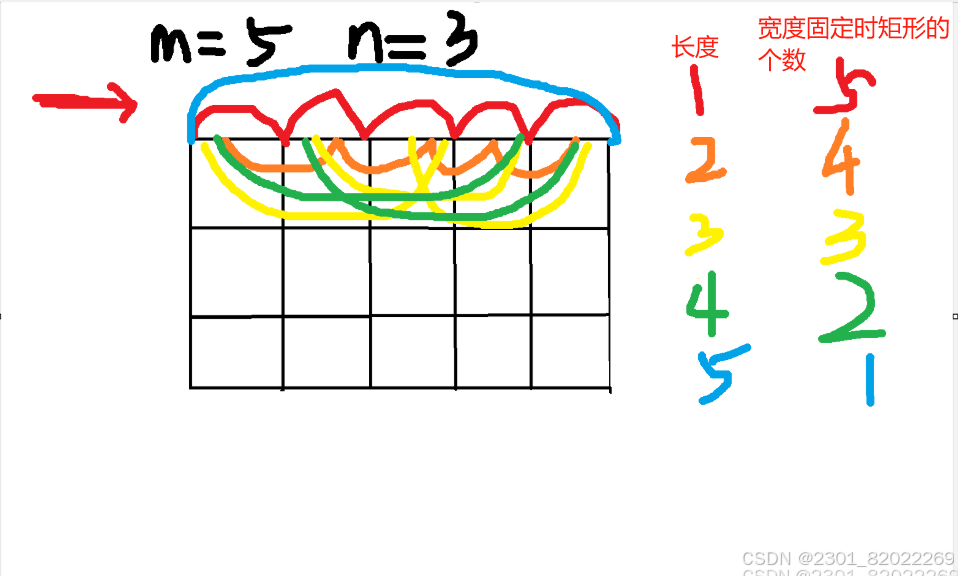
1.从水平方向上看，以长度为1个单位的线段为矩形长的矩形个数有m个；以长度为2个单位的线段为矩形长的矩形个数有m-1个；以长度为3个单位的线段为矩形长的矩形个数有m-2个；……；以长度为m个单位的线段为矩形长的矩形个数有1个。那么水平方向上确定矩形长的不同组合方式总数为1+2+3+....+m.

2.在垂直方向上，以宽度为1个单位的线段为矩形宽的矩形个数有n个；以宽度为2个单位的线段为矩形宽的矩形个数有n-1个；以宽度为3个单位的线段为矩形宽的矩形个数有n-2个；……；以宽度n为个单位的线段为矩形宽的矩形个数有1个。所以垂直方向上确定矩形宽的不同组合方式总数为1+2+3+....+n.

3.因为确定一个矩形需要从水平方向确定长和从垂直方向确定宽这两个独立的过程。根据乘法原理，矩形的总数就是水平方向确定矩形长的方法数与垂直方向确定矩形宽的方法数的乘积。所以矩形的总数为（1+2+3+....+n）*(1+2+3+....+m)。

边长为k的正方形数的计算公式：（n-(k-1)）*（m-(k-1)）

对于正方形数量的推导:

1. 边长为1的正方形数量
   • 边长为1的正方形，在长为m，宽为n（假设m>n，不影响一般性）的矩形网格中，每行有m个，一共有n行，所以边长为的正方形数量是m*n个。
2. 边长为2的正方形数量
   • 边长为2的正方形，在水平方向上，要形成边长为的正方形，其起始位置从左到右能放置的数量为m-1个（因为要保证右边还有一个单位长度形成边长为2的正方形），举例如下图所示
   • 同理，在垂直方向上，能放置的数量为n-1个（保证下边还有一个单位长度形成边长为的正方形）。所以边长为的正方形数量是（m-1）*(n-1)个。

长方形数=矩形数-正方形数

由于计算矩形数和正方形数时超过了int的取值范围所以采取long long类型（输入输出格式均为%lld）

代码展示：

#include<stdio.h>
int main(){
	long long n,m,min;
	long long squre,rectant,sum;
	scanf("%lld %lld",&n,&m);
	sum=(((1+n)*n)/2)*(((1+m)*m)/2);
	squre=0;
	if(m>n)min=n;
	else min=m;
	for(int i=0;i<min;i++){
		squre+=(n-i)*(m-i);
	}
	rectant=sum-squre;
	printf("%lld %lld\n",squre,rectant);
	return 0;
}