【C++】AVL树的模拟实现

最新推荐文章于 2024-06-13 23:56:26 发布

枫挽月

最新推荐文章于 2024-06-13 23:56:26 发布

阅读量728

点赞数 17

文章标签：数据结构

本文链接：https://blog.csdn.net/2302_76142697/article/details/138856018

版权

一、AVL树的概念：

在前面二叉搜索树中我们讲到过，在进行查找操作时：理想状态下只需搜索高度次即可完成查找，也就是时间复杂度O(logn) 。但是如果表中数据本来就是有序或者接近有序的话，此时的二叉搜索树就会退化成单支树，就相当于在顺序表中搜索元素，效率就会变得非常低下O(n)，如图:

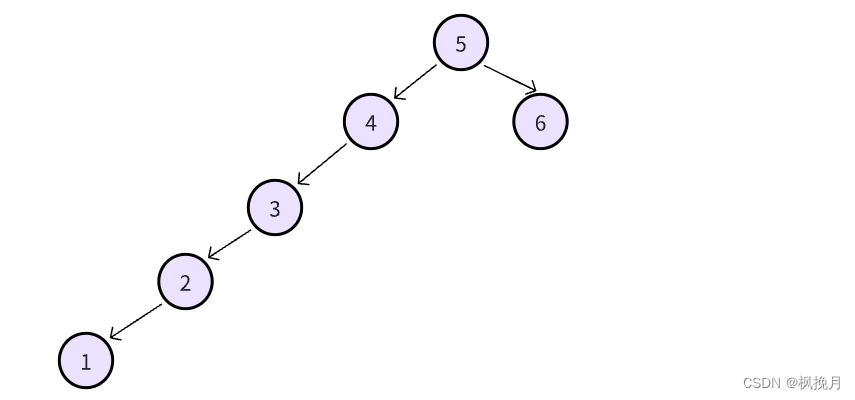
为了解决这个问题，此时就“诞生”了AVL树，AVL树的特性就是：

它的左子树和右子树的高度之差的绝对值不能超过 1 。
它的左右子树也都是AVL树。

左右子树的高度差也被简称为平衡因子，那么怎么更新平衡因子呢？

以下设定为新插入节点为cur，cur指向的父节点为parent。

1、设置每个新插入的节点的平衡因子为0。

2、当插入节点cur时，如果是在parent节点的左边插入，那么parent节点的平衡因子-1，如果是在parent的右边插入，则parent的平衡因子+1。

3、更新完平衡因子后如果parent的平衡因子为2或-2时就违反了AVL树的规则（左右子树的高度差的绝对值不超过 1），此时就要进行旋转操作，至于旋转操作等到后面实现的时候再讲。

4、如果没有违反规则，那么就看一下parent的平衡因子否等于 0 ，（因为平衡因子只有-1、0、1三种情况），如果等于则结束并完成了插入操作，如果不等于则要继续往上更新，就要检查一下parent的父节点的平衡因子是否违法了规则以此反复，也就是cur变成parent，parent变成parent的父节点。

下面看一下一个AVL树图（每个节点的平衡因子用红字标注）：

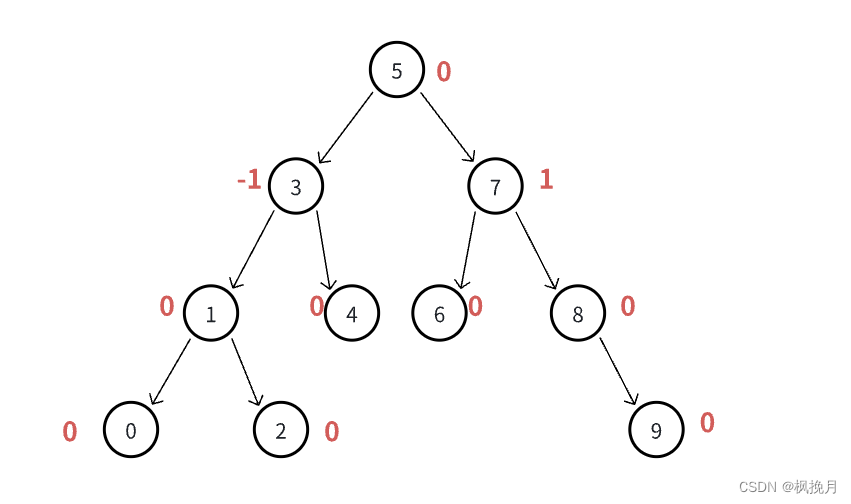
此时我们可以看到，虽然数据有序，但是该树并没有退化成单支树，而是一颗AVL树，它的高度是平衡的，保持在O(logn)，此时的搜索效率就非常高了。

二、AVL树的模拟实现：

1、定义树节点：

对于AVL树的节点，我们可以使用一个三叉链表来控制父节点与左右孩子节点的链接，然后将每一个新插入节点的平衡因子_bf置为零。

template<class K, class V>
struct AVLTreeNode
{
	AVLTreeNode<K, V>* _left;    // 左孩子
	AVLTreeNode<K, V>* _right;   // 右孩子
	AVLTreeNode<K, V>* _parent;  // 父节点
	pair<K, V> _kv; // <key, value> 键值对

	int _bf; // 平衡因子

    // 节点的构造函数
	AVLTreeNode(const pair<K, V>& kv)
		:_left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _kv(kv)
		, _bf(0)
	{}

};

2、AVL树的插入操作：

对于AVL树的插入，如果插入节点后并没有违反规则（也就是导致有节点的平衡因子为2 / -2），则直接插入结束，如果说违反了规则那么树就会失衡，需要进行旋转操作，失衡情况有如下四种：

（下面表示：红色节点为插入节点cur，绿色节点为插入节点的父节点parent，黄色节点为父节点的父节点grandfather。平衡因子为2 / -2 统称为失衡节点）

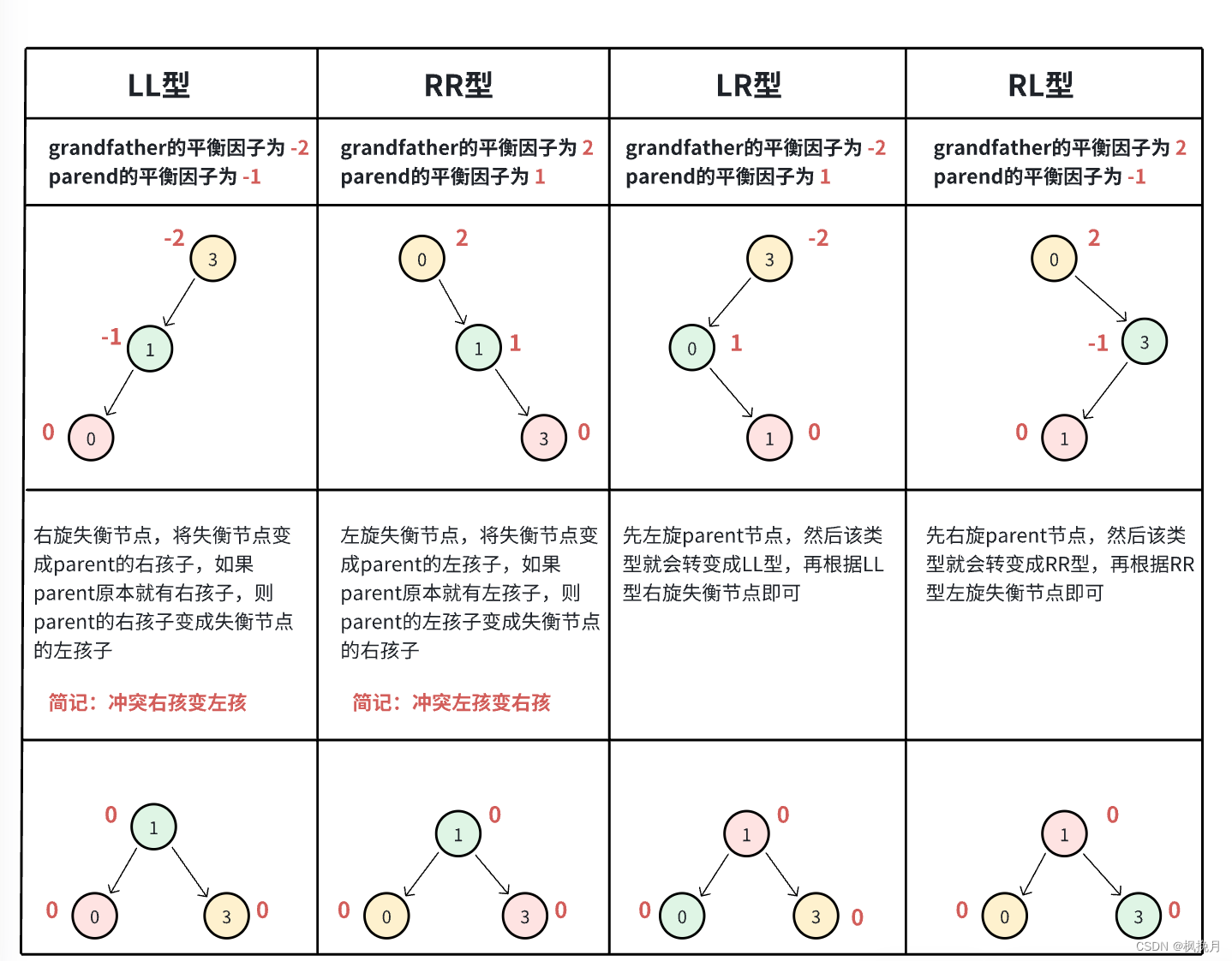
将以上情况转换成代码形式如下：

// 插入删除效率其实就是查找效率logN
bool Insert(const pair<K, V>& kv)
{
	if (_root == nullptr) // 如果树为空，那么插入节点就是根节点
	{
		_root = new Node(kv);
		return true;
	}

	// 设置插入节点与其父节点
	Node* parent = nullptr;
	Node* cur = _root;

	while (cur)// 将cur节点遍历到空位置（也就是插入位置）
	{
		if (cur->_kv.first < kv.first)
		{
			parent = cur;
			cur = cur->_right;
		}
		else if (cur->_kv.first > kv.first)
		{
			parent = cur;
			cur = cur->_left;
		}
		else // cur->_kv.first == kv.first 
		{
			return false; // 插入重复值不做处理
		}
	}

	// 更新cur节点是parent的左节点还是右节点
	cur = new Node(kv);
	if (parent->_kv.first < kv.first) { parent->_right = cur; }
	else { parent->_left = cur; }
	cur->_parent = parent;

	// 更新平衡因子直到为0或者到根节点
	while (parent)
	{
		if (cur == parent->_left) { parent->_bf--; }
		else { parent->_bf++; }

		// 如果平衡因子为 0 则证明当前平衡
		if (parent->_bf == 0) { break; }

		// 如果平衡因子为1 / -1则继续往上更新
		else if (parent->_bf == 1 || parent->_bf == -1)
		{
			cur = parent;
			parent = parent->_parent;
		}

		// 平衡因子为 2 / -2，判别是四种情况的哪一种，然后根据情况进行旋转操作
		else if (parent->_bf == 2 || parent->_bf == -2)
		{
			if (parent->_bf == -2 && cur->_bf == -1) // LL型
			{
				RotateR(parent);
			}
			else if (parent->_bf == 2 && cur->_bf == 1)// RR型
			{
				RotateL(parent);
			}
			else if (parent->_bf == -2 && cur->_bf == 1) // LR型
			{
				RotateLR(parent);
			}
			else if (parent->_bf == 2 && cur->_bf == -1) // RL型
			{
				RotateRL(parent);
			}
			break;
		}

		// 正常来讲就只有以上情况，如果平衡因子不在 [-2 ~ 2]的区间内就证明有问题，直接在这做个保险
		else
		{
			assert(false);
		}
	}
	return true;
}

3、AVL树的旋转操作：

注意：如下函数的参数传入的是失衡节点，也就是parent参数不是插入节点的父节点，而直接是失衡节点，请注意这两者的不同！！！

LL型：

LL型失衡，就是对失衡节点进行右单旋操作：

void RotateR(Node* parent)
{
	// 记录旋转点位置，旋转点也就是失衡节点的左孩子
	Node* subL = parent->_left;

	// 旋转点右孩子位置
	Node* subLR = subL->_right;

	// 冲突右孩变左孩
	parent->_left = subLR;

	// 如果这个节点存在，则将它的父节点设置为失衡节点
	if (subLR)
		subLR->_parent = parent;

	// 将失衡节点设置为旋转点的右孩子
	subL->_right = parent;

	// 记录失衡节点的父节点，要将旋转点的父节点设置为ppNode，但如果失衡节点为根节点，则ppNode为空
	Node* ppNode = parent->_parent;
	parent->_parent = subL;

	// 如果失衡节点是根节点，则将根节点设置为旋转点
	if (parent == _root)
	{
		_root = subL;
		_root->_parent = nullptr;
	}
	else // 失衡节点不是根节点，则更新ppNode的关系
	{
		if (ppNode->_left == parent)
		{
			ppNode->_left = subL;
		}
		else
		{
			ppNode->_right = subL;
		}

		subL->_parent = ppNode;
	}

	// 将平衡因子置为 0
	parent->_bf = subL->_bf = 0;
}

RR型：

RR型失衡，就是对失衡节点进行左单旋操作：

void RotateL(Node* parent)
{
	// 记录旋转点位置，旋转点也就是失衡节点的右孩子
	Node* subR = parent->_right;

	// 旋转点左孩子位置
	Node* subRL = subR->_left;

	// 冲突左孩变右孩
	parent->_right = subRL;

	// 如果这个节点存在，则将它的父节点设置为失衡节点
	if (subRL)
		subRL->_parent = parent;

	// 将失衡节点设置为旋转点的左孩子
	subR->_left = parent;

	// 记录失衡节点的父节点，要将旋转点的父节点设置为ppNode，但如果失衡节点为根节点，则ppNode为空
	Node* ppNode = parent->_parent;

	parent->_parent = subR;

	// 如果失衡节点是根节点，则将根节点设置为旋转点
	if (parent == _root)
	{
		_root = subR;
		_root->_parent = nullptr;
	}
	else // // 失衡节点不是根节点，则更新旋转点与ppNode的关系
	{
		if (ppNode->_right == parent)
		{
			ppNode->_right = subR;
		}
		else
		{
			ppNode->_left = subR;
		}
		subR->_parent = ppNode;
	}

	// 将平衡因子置为 0
	parent->_bf = subR->_bf = 0;
}

LR型：

LR型失衡，就是对失衡节点的左孩子进行左单旋操作，再对失衡节点进行右单旋操作（完成操作后请注意参与旋转的节点的平衡因子的更新，并不一定说平衡因子为 0）：

上面的图画的都是简单版本，实际上还有两种情况（注意看红色节点）

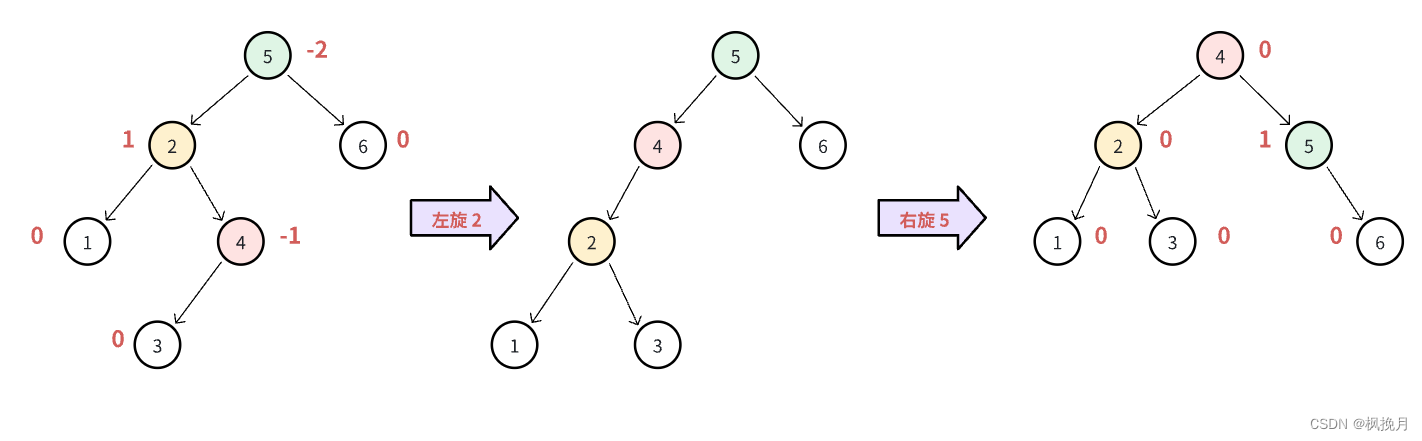
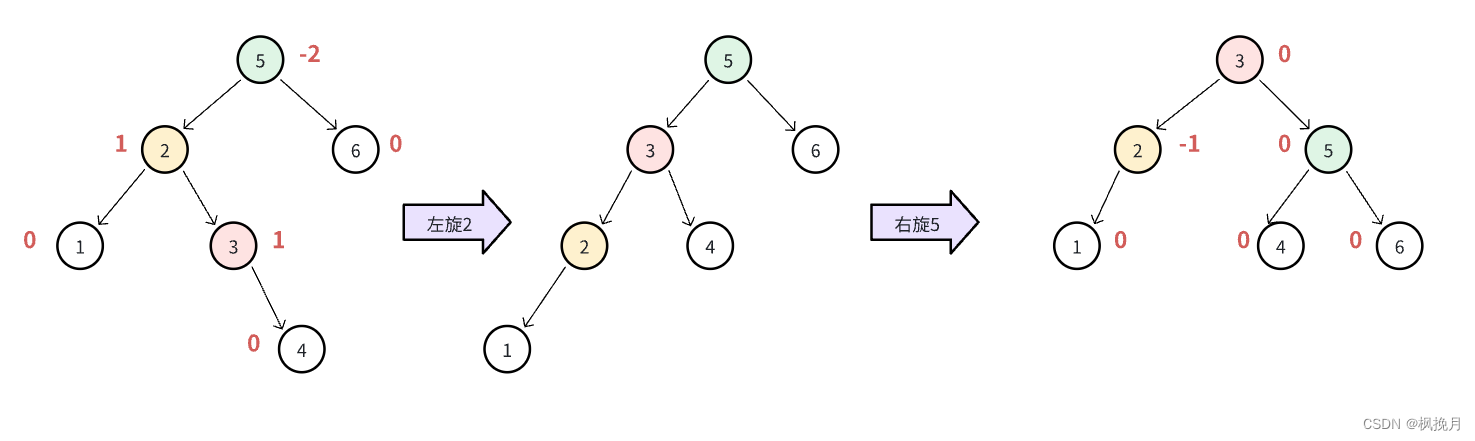
以上两种情况均属于LR型旋转，但是我们可以看到，参与旋转的三个有颜色的节点旋转完之后并不是全部的平衡因子都会归零，红色节点的平衡因子会影响到绿色和黄色节点的平衡因子，这是因为旋转完之后红色节点的左边会变成黄色节点的右边，红色节点的右边会变成绿色节点的左边，因此我们要特别记录下这个红色节点的平衡因子，在进行完旋转后要更新绿色 / 黄色节点的平衡因子：

void RotateLR(Node* parent)
	{
		// 失衡节点的左孩子节点
		Node* subL = parent->_left;

		// 左孩子节点的右孩子节点
		Node* subLR = subL->_right;

		// 记录subLR(红色节点)的平衡因子
		int bf = subLR->_bf;

		// 先左单旋失衡节点的左孩子(subL)，再有单旋失衡节点
		RotateL(parent->_left);
		RotateR(parent);

		// 根据subLR的平衡因子更新参与旋转节点（绿色 / 黄色节点）的平衡因子
		// 这里注释掉的最好写上，不写也没关系，因为对应左旋和右旋函数里是写了将全部平衡因子更新为0的
		// 写上是为了提高可读性和降低与左右旋函数的依赖性
		if (bf == -1)
		{
			/*subLR->_bf = 0;
			subL->_bf = 0;*/

			parent->_bf = 1;
		}
		else if (bf == 1)
		{
			/*parent->_bf = 0;
			subLR->_bf = 0;*/

			subL->_bf = -1;
		}
		else if (bf == 0)
		{
			/*parent->_bf = 0;
			subL->_bf = 0;
			subLR->_bf = 0;*/
		}
		else
		{
			assert(false); // 除这三种情况外没有其他情况
		}
	}

RL型：

RL型失衡，就是对失衡节点的右孩子进行右单旋操作，再对失衡节点进行左单旋操作（完成操作后请注意参与旋转的节点的平衡因子的更新，并不一定说平衡因子为 0）：

跟上面LR型介绍的情况应用，还有两种情况，其实本质上是一样的，只不过换了一种方向，这里就只给出图了，就不再重复介绍了。

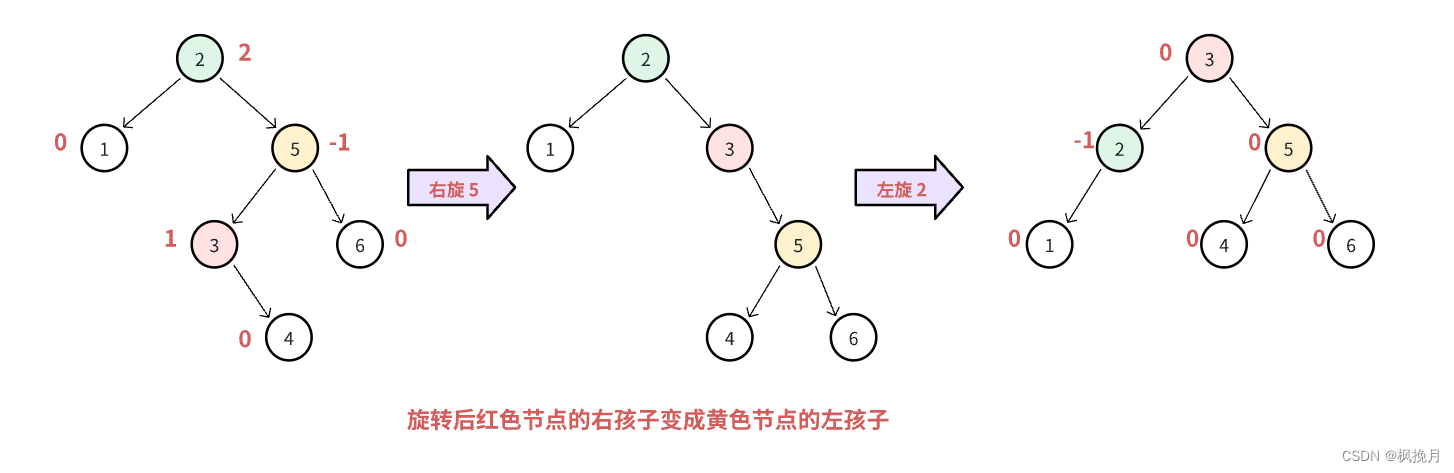
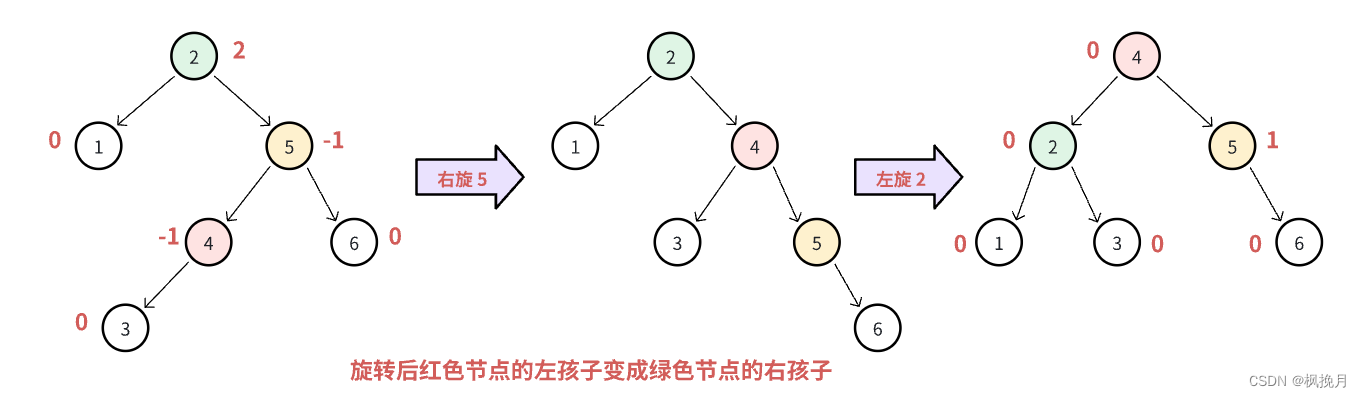
这里也是一样要注意红色节点的平衡因子对黄色 / 绿色节点的影响

void RotateRL(Node* parent)
{
	Node* subR = parent->_right;
	Node* subRL = subR->_left;

	int bf = subRL->_bf;

	RotateR(parent->_right);
	RotateL(parent);

	if (bf == 1)
	{
		/*subR->_bf = 0;
		subRL->_bf = 0;*/

		parent->_bf = -1;
	}
	else if (bf == -1)
	{
		/*parent->_bf = 0;
		subRL->_bf = 0;*/

		subR->_bf = 1;
	}
	else if (bf == 0)
	{
		/*parent->_bf = 0;
		subR->_bf = 0;
		subRL->_bf = 0;*/
	}
	else
	{
		assert(false); // 除这三种情况外没有其他情况
	}
}