【机器学习】从线性回归模型看一个简单的成本函数

• 🌸博主主页：@釉色清风
• 🌸文章专栏：机器学习
• 🌸今日语录：事情不做，越想越难；事情做了，越做越容易。

🌾🌾在上一篇文章中，我们用波特兰房屋面积大小与价格的关系，建立了线性回归模型。同时，在上篇文章中，我们基本了解到了机器学习中的专业名词以及符号表示。在这一次，同样又根据吴恩达老师的机器学习过程，总结成本函数(代价函数)，这是很重要的，因为成本函数将告诉我们模型的运行情况，可以帮助我们尝试将模型做得更好。希望对大家有帮助。

🌼引入：模型参数

我们仍然以上一篇文章中的例子作为切入。

我们的训练集包含输入特征(input features)x和输出目标(output targets)y。
我们选定来拟合这个训练集的模型是线性函数。即：
$$Model:f_{w,b}(x)=wx+b$$
其中，参数$w$和$b$被称为模型参数。
以我们之前中学的知识，我们知道$w$和$b$是待定参数，即变量。同样，在机器学习中也是如此。$w$ 和$b$作为模型的参数，是我们可以在训练期间可以改进模型的变量。

🌼模型参数如何影响我们的模型

作为参数$w$和$b$到底会怎样影响我们的模型呢？

下面，我们通过简单的几种特殊情况的很简单的例子来看一下：

即简单的说明，$w$和$b$的取值影响我们的"线",即影响我们的模型。

而对于我们的数据集，和我们定下的线性回归模型，我们需要选择$w$和$b$的值，以便我们的得到的函数f可以更好地拟合我们的数据。

（其中$\hat{y}$是模型的预测值。）

这条直线，在视觉上，我们看起来是相符的，但是这粗略的判断或者大概的估计，是不严谨的，我们并不能通过“视觉观察”来寻求$w$和$b$的最优值。

所以，我们现在的问题，产生了，如何找到$w$和$b$的值，使得尽可能多的训练示例$x_i$、$y_i$的预测值${\hat{y}}_i$接近真实目标$y_i$,使得拟合效果尽可能地好。

🌼评价拟合效果——成本函数(Cost function)

那么现在怎么评价拟合效果尽可能地好呢？如何衡量拟合的结果呢？
为此，我们将构建一个成本函数(Cost function)。
成本函数其实就是，采用预测的${\hat{y}}_i$减去目标值$y$，这样进行预测值和原真值的一个比较，即就是计算误差，测量预测与目标的距离。

但是如上，这样的误差可能是正、也可能是负，在数学中，衡量整体而非单个的误差，我们都要计算误差的绝对值或者平方(一般都是平方)。

通写如此。我们要为训练集中的不同训练示例i计算此项，即：

为了构建一个不会随着训练集大小而自动变大的成本函数，我们将计算平均平方误差而不是总平均误差，我们采用对每一个训练示例的误差求和再平均。
即：

按照惯例，机器学习使用的成本函数实际上时在上面此基础上再除以2，额外除以2只是为了让我们后面的一些计算看起来更加整洁。

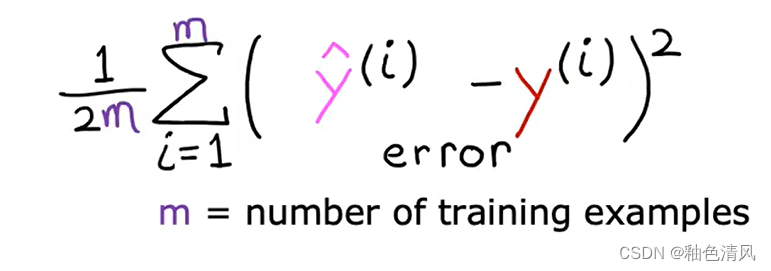
成本函数，我们一般用J来代表成本函数，即：

$J(w,b)$这也称为平均误差成本函数。
在上述式子中,${\hat{y}}^{(i）}$是预测值，可以写作为$f_{w,b}(x^{(i)})$。故成本函数$J$就可以写成了：

在机器学习中，不同的人会针对不同的应用程序使用不同的成本函数，但平方误差成本函数$J(w,b)$是迄今为止线性回归最常用的函数。就此而言，对于所有的回归问题，它似乎为许多应用程序提供了良好的结果。