本篇文章的分支限界法会与前一篇文章的回溯法进行一个对比,感兴趣的同学可以点击链接查看回溯算法文章哦!!!
https://blog.csdn.net/2302_76516899/article/details/138923149
目录
🐘分支限界法
- 分支限界法是一种解决组合优化问题的算法,它与回溯算法类似,但在搜索解空间时采用了一些优化策略,以降低时间复杂度并提高搜索效率。
🦁分支限界法核心思想
- 分支限界法的核心思想是通过不断划分问题的解空间,并使用一些启发式策略,尽早地排除一些不可能产生最优解的分支,从而缩小搜索空间,提高搜索效率。
🦁解题步骤
🐱建立搜索树
- 首先建立一个搜索树,树的每个节点表示问题的一个部分解,根节点表示空解或初始解,叶节点表示完整解。
🐱分支扩展
- 对于搜索树中的每个节点,根据问题的约束条件,生成其子节点,即通过一定的规则对当前节点进行扩展,得到更多可能的解。
🐱界限计算
- 对于每个节点,计算一个上界(优化问题)或下界(最小化问题),该界限用于判断该节点的子节点是否有可能产生更优的解。
🐱剪枝策略
- 根据界限计算的结果,采取一些剪枝策略,即排除一些不可能产生最优解的节点或子树,从而减少搜索空间。
🐱回溯和迭代
- 在搜索过程中,不断回溯到父节点并尝试其他分支,直到找到满足条件的解或遍历完整个搜索树。
通过以上步骤,分支限界法能够逐步缩小解空间,提高搜索效率,并最终找到满足条件的最优解。
🐘示例
🐱问题
假设有如下的背包问题:
- 物品重量:
[2, 3, 4, 5]- 物品价值:
[3, 4, 5, 6]- 背包容量:
8
🐱树状图解释
🐟根节点 (Level 0)
- 状态:未选中任何物品
- 重量:0
- 价值:0
🐟Level 1:
- 左子节点:选择第1个物品
- 重量:2
- 价值:3
- 右子节点:不选择第1个物品
- 重量:0
- 价值:0
🐟Level 2:
- 左子节点:选择第2个物品
- 重量:5
- 价值:7
- 右子节点:不选择第2个物品
- 重量:2
- 价值:3
- 左子节点:选择第2个物品
- 重量:3
- 价值:4
- 右子节点:不选择第2个物品
- 重量:0
- 价值:0
🐱代码图解(python)
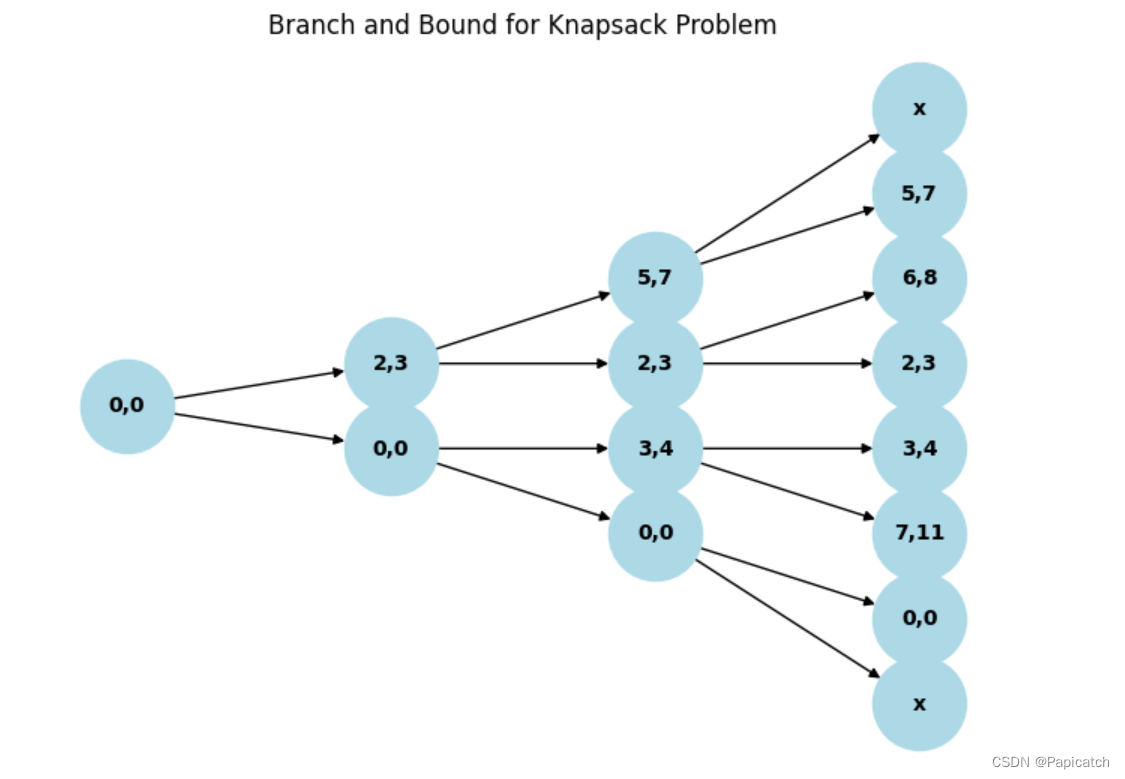
以下是上述树状图的示例图示:
import matplotlib.pyplot as plt
import networkx as nx
def draw_knapsack_branch_and_bound():
G = nx.DiGraph()
# 添加节点和节点的标签(表示当前的重量和价值)
nodes = [
("0", "0,0", 0),
("1L", "2,3", 1), ("1R", "0,0", 1),
("2LL", "5,7", 2), ("2LR", "2,3", 2), ("2RL", "3,4", 2), ("2RR", "0,0", 2),
("3LLL", "x", 3), ("3LLR", "5,7", 3), ("3LRL", "6,8", 3), ("3LRR", "2,3", 3),
("3RLL", "3,4", 3), ("3RLR", "7,11", 3), ("3RRL", "0,0", 3), ("3RRR", "x", 3)
]
# 添加节点
for node, label, subset in nodes:
G.add_node(node, label=label, subset=subset)
# 添加边
edges = [
("0", "1L"), ("0", "1R"),
("1L", "2LL"), ("1L", "2LR"), ("1R", "2RL"), ("1R", "2RR"),
("2LL", "3LLL"), ("2LL", "3LLR"), ("2LR", "3LRL"), ("2LR", "3LRR"),
("2RL", "3RLL"), ("2RL", "3RLR"), ("2RR", "3RRL"), ("2RR", "3RRR")
]
# 添加边
for edge in edges:
G.add_edge(*edge)
# 使用multipartite_layout布局
pos = nx.multipartite_layout(G, subset_key="subset")
labels = nx.get_node_attributes(G, 'label')
nx.draw(G, pos, with_labels=True, labels=labels, node_size=2000, node_color='lightblue', font_size=10, font_weight='bold', arrows=True)
plt.title("Branch and Bound for Knapsack Problem")
plt.show()
# 画图演示分支限界法解决0-1背包问题的过程
draw_knapsack_branch_and_bound()
🐱运行结果
🦁完整代码实现(C++)
🐱代码如下
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
struct Item {
int weight;
int value;
};
struct Node {
int level;
int profit;
int weight;
float bound;
};
float bound(Node u, int n, int W, std::vector<Item>& items) {
if (u.weight >= W) return 0;
float profit_bound = u.profit;
int j = u.level + 1;
int total_weight = u.weight;
while (j < n && total_weight + items[j].weight <= W) {
total_weight += items[j].weight;
profit_bound += items[j].value;
j++;
}
if (j < n)
profit_bound += (W - total_weight) * items[j].value / (float)items[j].weight;
return profit_bound;
}
void knapsack(int W, std::vector<Item>& items, int n) {
std::sort(items.begin(), items.end(), [](Item a, Item b) {
return (float)a.value / a.weight > (float)b.value / b.weight;
});
std::queue<Node> Q;
Node u, v;
u.level = -1;
u.profit = u.weight = 0;
Q.push(u);
int maxProfit = 0;
while (!Q.empty()) {
u = Q.front();
Q.pop();
if (u.level == -1)
v.level = 0;
if (u.level == n - 1)
continue;
v.level = u.level + 1;
v.weight = u.weight + items[v.level].weight;
v.profit = u.profit + items[v.level].value;
if (v.weight <= W && v.profit > maxProfit)
maxProfit = v.profit;
v.bound = bound(v, n, W, items);
if (v.bound > maxProfit)
Q.push(v);
v.weight = u.weight;
v.profit = u.profit;
v.bound = bound(v, n, W, items);
if (v.bound > maxProfit)
Q.push(v);
}
std::cout << "Maximum profit is: " << maxProfit << std::endl;
}
int main() {
int W = 10; // 背包容量
std::vector<Item> items = { {2, 10}, {3, 5}, {5, 15}, {7, 7}, {1, 6}, {4, 18}, {1, 3} };
int n = items.size();
knapsack(W, items, n);
return 0;
}
🐱代码解释
-
结构体定义:
Item结构体用于表示每个物品的重量和价值。Node结构体用于表示搜索树中的节点,包括当前节点的层级、当前的利润、当前的重量和界限。
-
界限计算函数:
bound函数用于计算节点的界限,即在当前节点的基础上,最大可能的利润。
-
主算法函数:
knapsack函数是分支限界法的实现。首先对物品按单位重量价值排序,然后使用队列来实现广度优先搜索。- 在每个节点,根据是否选择当前物品生成两个子节点,并计算它们的界限。
- 如果节点的界限大于当前已知的最大利润,将其加入队列。
-
主函数:
- 初始化背包容量和物品列表,然后调用
knapsack函数计算最大利润。
- 初始化背包容量和物品列表,然后调用
🐱运行截图
🐘分支限界法效率
- 分支限界法的时间复杂度和空间复杂度取决于具体问题的规模以及剪枝效率。
🦁时间复杂度
- 在最坏情况下,分支限界法可能需要探索所有可能的子集。这意味着时间复杂度可能接近于穷举搜索,即 O(2^n),其中 n 是物品的数量。
- 然而,由于分支限界法通过剪枝来减少搜索空间,实际运行时间通常远小于最坏情况。剪枝的效率取决于选择的界限函数和排序策略。如果剪枝策略非常有效,实际搜索的节点数量可能大大减少,从而显著降低实际运行时间。
🦁空间复杂度
- 分支限界法的空间复杂度主要由存储搜索树的节点所需的内存决定。在最坏情况下,队列中可能包含所有可能的节点,因此空间复杂度也可能接近于 O(2^n)。
- 实际使用中,空间复杂度取决于具体的实现方式和剪枝效率。如果剪枝策略有效,队列中的节点数会大幅减少,从而降低实际的空间需求。
🦁总结
- 分支限界法通过有效的剪枝策略,可以显著减少需要搜索的节点数量,从而降低时间复杂度和空间复杂度。虽然在最坏情况下,这些复杂度仍然可能接近于穷举搜索,但在实际问题中,分支限界法通常表现得更高效。
- 对于大规模问题,选择合适的界限函数和排序策略至关重要,因为它们直接影响剪枝的效率和算法的实际性能。
🐘分支限界法优缺点
🦁优点
-
求解最优解: 分支限界法能够找到问题的最优解,而不仅仅是一个可行解。这使得它在许多实际应用中非常有价值。
-
剪枝优化: 分支限界法通过界限函数和剪枝策略,可以大幅减少需要探索的节点数,避免不必要的计算,提高算法效率。
-
广泛适用性: 分支限界法适用于各种组合优化问题,如0-1背包问题、旅行商问题、作业调度问题等。
-
系统性搜索: 通过系统地遍历搜索树,分支限界法确保不会遗漏任何可能的解,同时可以逐步逼近最优解。
🦁缺点
-
时间复杂度高: 在最坏情况下,分支限界法需要遍历所有可能的子集,其时间复杂度接近于穷举搜索,即 O(2n)。对于大规模问题,运行时间可能非常长。
-
空间复杂度高: 在最坏情况下,分支限界法需要存储所有可能的节点,其空间复杂度也可能接近于 O(2n)。这会导致在内存需求方面的瓶颈,特别是对于大规模问题。
-
依赖于界限函数: 分支限界法的效率高度依赖于界限函数的设计。如果界限函数设计不合理,剪枝效果不好,算法性能会显著下降。
-
实现复杂: 与其他简单的启发式算法相比,分支限界法的实现相对复杂,需要仔细设计和调试界限函数和剪枝策略。
🦁结论
- 分支限界法通过剪枝策略和系统性搜索,能够有效地求解组合优化问题的最优解。然而,由于其时间复杂度和空间复杂度在最坏情况下仍然很高,对于大规模问题可能会面临性能瓶颈。选择合适的界限函数和剪枝策略可以显著提高算法的实际效率,使其在许多实际应用中表现良好。
- 总体而言,分支限界法是一种强大但复杂的算法,适用于需要求解最优解的复杂组合优化问题。在实际应用中,需要根据具体问题的特点和规模,权衡其优缺点,选择最合适的求解方法。
🐘回溯法与分支限界法异同点
🦁相同点
🐱搜索策略
- 系统性搜索: 两种方法都使用系统性搜索策略,遍历解空间,确保所有可能的解都能被考虑到。
- 递归和回溯: 两种方法通常都使用递归和回溯机制来探索和返回不同的解路径。
🐱适用问题
- 组合优化问题: 两种方法都适用于解决组合优化问题,如0-1背包问题、旅行商问题等。
- 解空间遍历: 它们都通过遍历解空间来找到最优解或满足约束条件的解。
🦁不同点
🐱剪枝策略:
- 回溯法: 回溯法主要依靠约束条件来剪枝,提前停止搜索不满足约束条件的路径。
- 分支限界法: 分支限界法不仅依靠约束条件,还使用界限函数(bound function)来估计当前路径可能的最优值,从而更加有效地剪枝,排除不可能产生最优解的路径。
🐱目标和效率:
- 回溯法: 回溯法主要关注找到所有满足条件的解,时间复杂度在最坏情况下可能是指数级。它没有特别针对优化问题进行优化,通常在所有可能的解中找到满足约束的解。
- 分支限界法: 分支限界法旨在找到最优解,利用界限函数进行有效的剪枝,通常能够比回溯法更快地逼近最优解,减少无效搜索,提高效率。
🐱实现复杂度:
- 回溯法: 实现相对简单,主要是通过递归和条件判断进行搜索和回溯。
- 分支限界法: 实现较为复杂,需要设计和计算界限函数,利用优先队列或其他数据结构来维护搜索过程中的节点。
🐱搜索方式:
- 回溯法: 回溯法通常使用深度优先搜索(DFS)策略,从根节点开始,深入到底部,然后回溯。
- 分支限界法: 分支限界法通常使用广度优先搜索(BFS)或基于优先队列的搜索策略,按照界限函数的值来决定搜索的优先级。
🦁示例对比
🐱回溯法解决0-1背包问题的伪代码:
void knapsack(int i, int profit, int weight) {
if (weight <= W && profit > maxProfit) {
maxProfit = profit;
}
if (i == n) return;
knapsack(i + 1, profit + values[i], weight + weights[i]);
knapsack(i + 1, profit, weight);
}
🐱分支限界法解决0-1背包问题的伪代码:
float bound(Node u) {
if (u.weight >= W) return 0;
float profit_bound = u.profit;
int j = u.level + 1;
int total_weight = u.weight;
while (j < n && total_weight + weights[j] <= W) {
total_weight += weights[j];
profit_bound += values[j];
j++;
}
if (j < n) {
profit_bound += (W - total_weight) * values[j] / (float)weights[j];
}
return profit_bound;
}
void knapsack() {
sort(items.begin(), items.end(), cmp);
queue<Node> Q;
Node u, v;
u.level = -1;
u.profit = u.weight = 0;
Q.push(u);
while (!Q.empty()) {
u = Q.front(); Q.pop();
if (u.level == -1) v.level = 0;
if (u.level == n - 1) continue;
v.level = u.level + 1;
v.weight = u.weight + weights[v.level];
v.profit = u.profit + values[v.level];
if (v.weight <= W && v.profit > maxProfit) {
maxProfit = v.profit;
}
v.bound = bound(v);
if (v.bound > maxProfit) {
Q.push(v);
}
v.weight = u.weight;
v.profit = u.profit;
v.bound = bound(v);
if (v.bound > maxProfit) {
Q.push(v);
}
}
}
🐱结论
回溯法和分支限界法都是强大的求解组合优化问题的工具。回溯法更简单直接,但在求解大规模优化问题时效率较低。分支限界法通过引入界限函数和剪枝策略,在求解最优解时通常更高效。选择哪种方法取决于具体问题的规模和优化需求。
希望这些能对刚学习算法的同学们提供些帮助哦!!!























 6748
6748

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








