高等数学第五章---定积分（§5.4反常积分）

§5.4 反常积分

前面我们学习了定积分 ${\int }_a^{b}f(x)dx$，其中积分区间 $[a,b]$ 是有限区间，且被积函数 $f(x)$ 在 $[a,b]$ 上是连续的（或至多有有限个第一类间断点，或分段连续）。这样的积分我们称之为正常积分 (或常义积分)，正常积分的值是存在的。

这一节我们将正常积分的概念进行推广，主要涉及两种情况：

1. 积分区间的推广：将有限区间 $[a,b]$ 推广到无限区间，如 $[a,+\infty )$, $(-\infty ,b]$, $(-\infty ,+\infty )$。这类积分称为无限区间上的反常积分 (或无穷限积分)。
2. 被积函数的推广：被积函数 $f(x)$ 在有限区间 $[a,b]$ 上无界 (即存在瑕点)。这类积分称为无界函数的反常积分 (或瑕积分)。

无限区间上的反常积分和无界函数的反常积分统称为广义积分或反常积分。

一、无限区间上的积分 (无穷限积分)

(1) 定义

定义 1： 设函数 $f(x)$ 在区间 $[a,+\infty )$ 上连续。如果对于任意 $t>a$，定积分 ${\int }_a^{t}f(x)dx$ 存在，并且极限
$$\underset{t\to +\infty }{\lim }{\int }_a^{t}f(x)dx$$
存在 (即为一个有限值)，则称此极限值为函数 $f(x)$ 在无穷区间 $[a,+\infty )$ 上的反常积分，记作
$${\int }_a^{+\infty }f(x)dx=\underset{t\to +\infty }{\lim }{\int }_a^{t}f(x)dx$$
此时，称反常积分 ${\int }_a^{+\infty }f(x)dx$ 收敛。如果上述极限不存在 (或为 $\infty$ 或 $-\infty$)，则称反常积分 ${\int }_a^{+\infty }f(x)dx$ 发散。

定义 2： 设函数 $f(x)$ 在区间 $(-\infty ,b]$ 上连续。如果对于任意 $t<b$，定积分 ${\int }_t^{b}f(x)dx$ 存在，并且极限
$$\underset{t\to -\infty }{\lim }{\int }_t^{b}f(x)dx$$
存在，则称此极限值为函数 $f(x)$ 在无穷区间 $(-\infty ,b]$ 上的反常积分，记作
$${\int }_{-\infty }^{b}f(x)dx=\underset{t\to -\infty }{\lim }{\int }_t^{b}f(x)dx$$
此时，称反常积分 ${\int }_{-\infty }^{b}f(x)dx$ 收敛。如果上述极限不存在，则称反常积分 ${\int }_{-\infty }^{b}f(x)dx$ 发散。

定义 3： 设函数 $f(x)$ 在区间 $(-\infty ,+\infty )$ 上连续。我们取任意实数 $a$ (通常取 $a=0$)，将积分拆分为两部分：
$${\int }_{-\infty }^{+\infty }f(x)dx={\int }_{-\infty }^{a}f(x)dx+{\int }_a^{+\infty }f(x)dx$$
如果右边的两个反常积分 ${\int }_{-\infty }^{a}f(x)dx$ 与 ${\int }_a^{+\infty }f(x)dx$ 都收敛，则称反常积分 ${\int }_{-\infty }^{+\infty }f(x)dx$ 收敛，其值为这两个收敛积分之和。如果右边的两个反常积分中至少有一个发散，则称反常积分 ${\int }_{-\infty }^{+\infty }f(x)dx$ 发散。

注： 利用上述定义，我们可以判断形如 ${\int }_a^{+\infty }f(x)dx$、${\int }_{-\infty }^{b}f(x)dx$ 和 ${\int }_{-\infty }^{+\infty }f(x)dx$ 的反常积分是否收敛，并在收敛时求出其值。

例 1

判别下列广义积分是否收敛，若收敛，并求其值。

$$(1){\int }_0^{+\infty }{e}^{-x}dx(2){\int }_0^{+\infty }x{e}^{-x^2}dx(3){\int }_{-\infty }^0\frac{1}{1+x^2}dx(4){\int }_{-\infty }^{+\infty }\frac{1}{1+x^2}dx(5){\int }_{-\infty }^0\cos xdx$$

解：

(2)
$$\begin{array}{rl}{\int }_0^{+\infty }x{e}^{-x^2}dx& =\underset{t\to +\infty }{\lim }{\int }_0^{t}x{e}^{-x^2}dx\\ & =\underset{t\to +\infty }{\lim }\left(-\frac{1}{2}{\int }_0^t{e}^{-x^2}d(-x^2)\right)\text{(令 }u=-x^2,du=-2xdx\text{)}\\ & =\underset{t\to +\infty }{\lim }\left[-\frac{1}{2}{e}^{-x^2}\right]{|}_0^t\\ & =\underset{t\to +\infty }{\lim }\left(-\frac{1}{2}{e}^{-t^2}-\left(-\frac{1}{2}{e}^0\right)\right)\\ & =\underset{t\to +\infty }{\lim }\left(-\frac{1}{2}{e}^{-t^2}+\frac{1}{2}\right)\\ & =-\underset{t\to +\infty }{\lim }\frac{1}{2e^{t^2}}+\frac{1}{2}\\ & =0+\frac{1}{2}=\frac{1}{2}\end{array}$$
所以，${\int }_0^{+\infty }x{e}^{-x^2}dx$ 收敛，其值为 $\frac{1}{2}$。

注：

1. 通过例 1 可以发现：利用定义判别无穷限积分的敛散性，其步骤是：
   • 先将被积函数 $f(x)$ 在有限区间上积分，得到一个变限积分（例如 ${\int }_a^{t}f(x)dx=F(t)-F(a)$）。
   • 然后对这个结果求极限（例如 ${\lim }_{t\to +\infty }(F(t)-F(a))$）。
2. 若反常积分 ${\int }_a^{+\infty }f(x)dx$ 收敛且 $f(x)\ge 0$，其几何意义可以理解为由曲线 $y=f(x)$、直线 $x=a$ 以及 $x$ 轴所围成的向右无限延伸的平面图形的面积。
3. 对于收敛的无穷限积分，牛顿-莱布尼兹公式在形式上仍然适用，即如果 $F^{\prime }(x)=f(x)$，则
   $${\int }_a^{+\infty }f(x)dx={F(x)|}_a^{+\infty }=\underset{x\to +\infty }{\lim }F(x)-F(a)$$
   $${\int }_{-\infty }^{b}f(x)dx={F(x)|}_{-\infty }^b=F(b)-\underset{x\to -\infty }{\lim }F(x)$$
   $${\int }_{-\infty }^{+\infty }f(x)dx={F(x)|}_{-\infty }^{+\infty }=\underset{x\to +\infty }{\lim }F(x)-\underset{x\to -\infty }{\lim }F(x)$$
   (对于第三种情况，需确保两个极限独立存在或通过拆分点计算)。
   当遇到不能直接代入 $\pm \infty$ 求值的情况时，实质上就是在求极限。

例 2

计算下列广义积分 (如果收敛)。

$$(1){\int }_0^{+\infty }{e}^{-x}dx(2){\int }_0^{+\infty }x{e}^{-x^2}dx(3){\int }_{-\infty }^{+\infty }\frac{1}{1+x^2}dx(4){\int }_e^{+\infty }\frac{1}{x\ln x}dx(5){\int }_1^{+\infty }\frac{1}{x+x^2}dx$$

解： (这里我们直接使用牛顿-莱布尼兹公式的推广形式)

(1)
$${\int }_0^{+\infty }{e}^{-x}dx=\left[-e^{-x}\right]{|}_0^{+\infty }=\underset{x\to +\infty }{\lim }(-e^{-x})-(-e^{-0})=0-(-1)=1$$

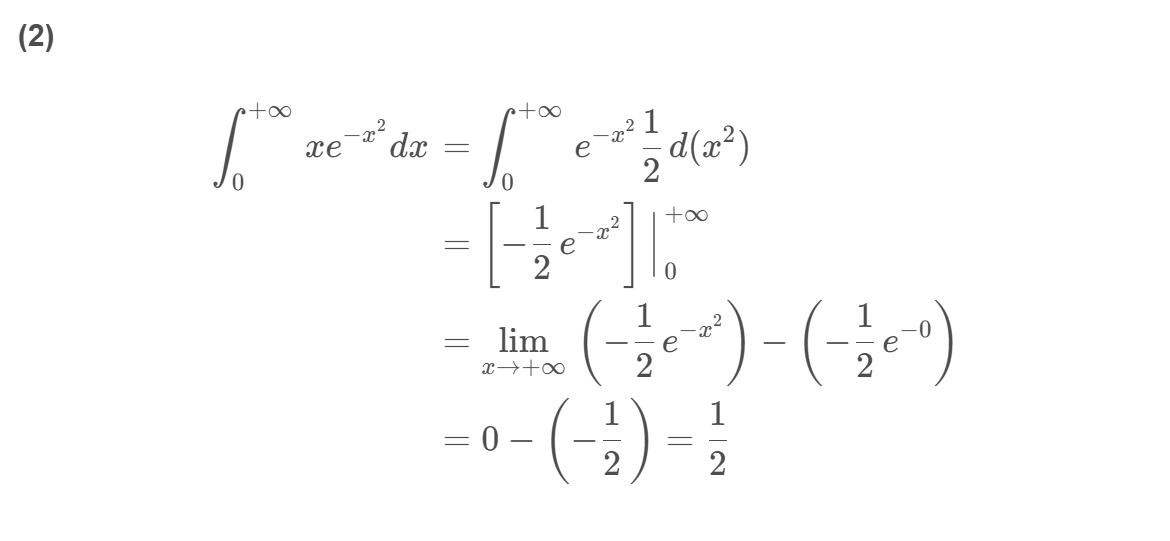
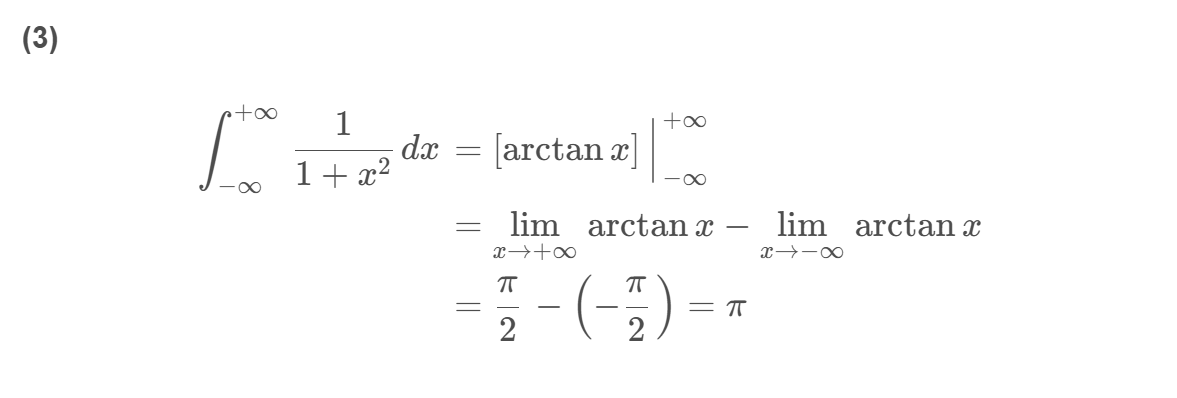
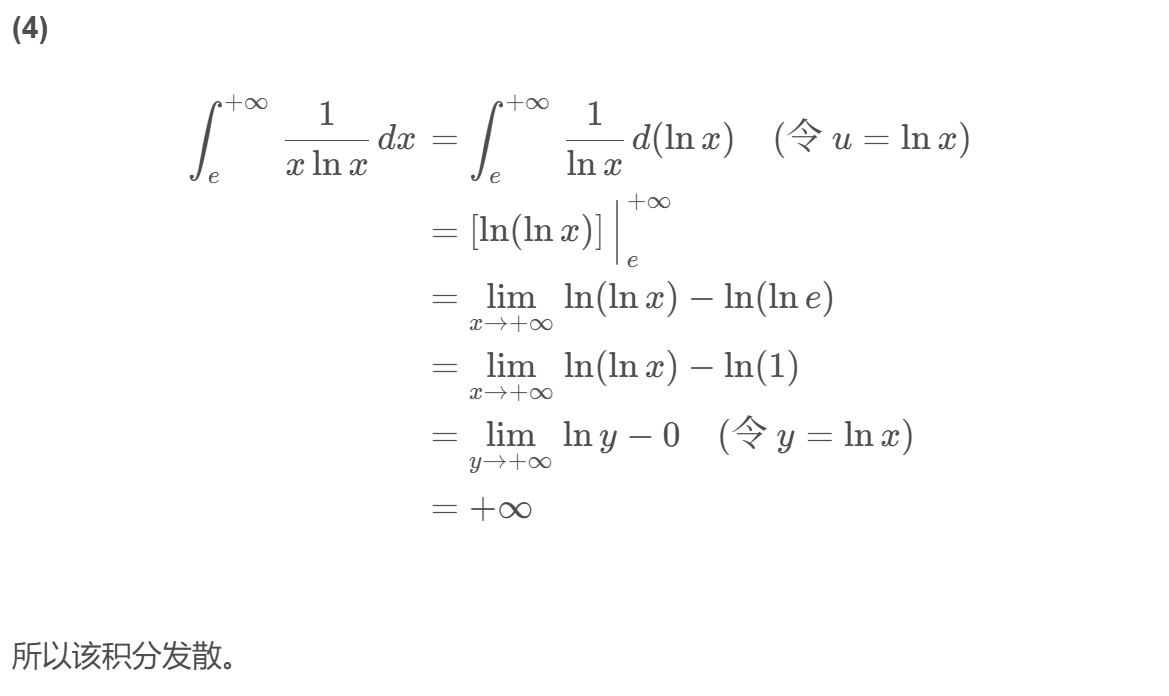
注： 通过上例可以发现：计算无穷限积分时，可以先不显式写出 ${\lim }_{t\to \infty }$，而是直接将被积函数的原函数求出来（这与正常定积分的计算方法是一样的，该凑微分凑微分，该换元就换元，该分部就分部），然后利用牛顿-莱布尼兹公式的推广形式，当积分限代入原函数求值时，若遇到“$\infty$”符号，则表示对该项求极限。这种方法在书写上比严格按定义计算要简便一些。

例 3 (p-积分)

证明反常积分 ${\int }_1^{+\infty }\frac{1}{x^p}dx$ (称为 p-积分)：

• 当 $p>1$ 时收敛，其值为 $\frac{1}{p-1}$。
• 当 $p\le 1$ 时发散。

证明：
因为当 $p=1$ 和 $p\ne 1$ 时，$\frac{1}{x^p}$ 的原函数形式不同，所以分情况讨论。

(1) 当 $p=1$ 时：
$${\int }_1^{+\infty }\frac{1}{x^p}dx={\int }_1^{+\infty }\frac{1}{x}dx=\left[\ln x\right]{|}_1^{+\infty }=\underset{x\to +\infty }{\lim }\ln x-\ln 1=+\infty -0=+\infty$$
所以当 $p=1$ 时，积分发散。

(2) 当 $p\ne 1$ 时：
$$\begin{array}{rl}{\int }_1^{+\infty }\frac{1}{x^p}dx& ={\int }_1^{+\infty }{x}^{-p}dx\\ & =\left[\frac{x^{-p+1}}{-p+1}\right]{|}_1^{+\infty }\\ & =\frac{1}{1-p}\left(\underset{x\to +\infty }{\lim }{x}^{1-p}-1^{1-p}\right)\\ & =\frac{1}{1-p}\left(\underset{x\to +\infty }{\lim }{x}^{1-p}-1\right)\end{array}$$
现在需要讨论 $1-p$ 的符号：

• 若 $p>1$，则 $1-p<0$。此时 ${\lim }_{x\to +\infty }{x}^{1-p}={\lim }_{x\to +\infty }\frac{1}{x^{p-1}}=0$。
  所以积分为 $\frac{1}{1-p}(0-1)=\frac{-1}{1-p}=\frac{1}{p-1}$。积分收敛。
• 若 $p<1$，则 $1-p>0$。此时 ${\lim }_{x\to +\infty }{x}^{1-p}=+\infty$。
  所以积分为 $\frac{1}{1-p}(+\infty -1)=+\infty$ (因为 $1-p>0$)。积分发散。

综合 (1) 和 (2) 可知：
p-积分 ${\int }_1^{+\infty }\frac{1}{x^p}dx$ 当 $p>1$ 时收敛 (值为 $\frac{1}{p-1}$)，当 $p\le 1$ 时发散。

注： 这个结论非常重要，应熟记，它常用于判断其他无穷限积分的敛散性 (通过比较判别法)。
例如：

• ${\int }_1^{+\infty }\frac{1}{x\sqrt{x}}dx={\int }_1^{+\infty }\frac{1}{x^{3/2}}dx$ 是收敛的，因为 $p=\frac{3}{2}>1$。
• ${\int }_1^{+\infty }\frac{1}{\sqrt[3]{x}}dx={\int }_1^{+\infty }\frac{1}{x^{1/3}}dx$ 是发散的，因为 $p=\frac{1}{3}<1$。

二、无界函数的积分（瑕积分）

(1) 瑕点 (Singular Points)

如果函数 $f(x)$ 在点 $x_0$ 的任一邻域内都无界，则称 $x_0$ 为函数 $f(x)$ 的一个瑕点 (或奇点)。
例如：

• 对于 $f(x)=\frac{1}{x}$，$x_0=0$ 是一个瑕点。
• 对于 $f(x)=\frac{1}{x^2-1}$，$x_0=1$ 和 $x_1=-1$ 都是瑕点。
• 对于 $f(x)=\ln x$，$x_0=0$ 是一个瑕点 (因为 ${\lim }_{x\to 0^{+}}\ln x=-\infty$)。

(2) 瑕积分 (Improper Integrals with Singularities)

如果定积分 ${\int }_a^{b}f(x)dx$ 的积分区间 $[a,b]$ 是有限的，但被积函数 $f(x)$ 在 $[a,b]$ 上有瑕点，则称此积分为无界函数的反常积分或瑕积分。
例如，${\int }_{-1}^1\frac{1}{x}dx$ 是一个瑕积分，因为积分区间 $[-1,1]$ 中包含瑕点 $x=0$。

注： 瑕积分 ${\int }_a^{b}f(x)dx$ 在形式上与正常积分 ${\int }_a^{b}f(x)dx$ 完全一样。因此，在学过瑕积分后，处理任何定积分 ${\int }_a^{b}f(x)dx$ 时，都要先检查被积函数在积分区间内是否有瑕点，以确定它究竟是正常积分还是瑕积分。

(3) 瑕积分 ${\int }_a^{b}f(x)dx$ 的收敛与发散

根据瑕点在积分区间的位置，有以下几种情况：

① 瑕点在积分区间的下限 $a$
设函数 $f(x)$ 在 $(a,b]$ 上连续，但在 $x=a$ 处无界 (即 $a$ 为瑕点，例如 ${\lim }_{x\to a^{+}}|f(x)|=\infty$) 。
如：${\int }_0^1\ln xdx$ (瑕点为 $x=0$)。

定义 1： 如果对于任意 $ϵ>0$ (且 $a+ϵ<b$)，积分 ${\int }_{a+ϵ}^{b}f(x)dx$ 存在，并且极限
$$\underset{ϵ\to 0^{+}}{\lim }{\int }_{a+ϵ}^{b}f(x)dx$$
存在 (为一个有限值)，则称此极限值为无界函数 $f(x)$ 在 $(a,b]$ 上的瑕积分，记作
$${\int }_a^{b}f(x)dx=\underset{ϵ\to 0^{+}}{\lim }{\int }_{a+ϵ}^{b}f(x)dx$$
若极限存在，称瑕积分 ${\int }_a^{b}f(x)dx$ 收敛；若极限不存在，称瑕积分发散。
(原文中使用 $t$ 作为 $ϵ$，这里统一使用 $ϵ$ 表示一个趋于0的小正量)

② 瑕点在积分区间的上限 $b$
设函数 $f(x)$ 在 $[a,b)$ 上连续，但在 $x=b$ 处无界 (即 $b$ 为瑕点)。
如：${\int }_0^a\frac{1}{\sqrt{a^2-x^2}}dx$ (瑕点为 $x=a$, 假设 $a>0$)。

定义 2： 如果对于任意 $ϵ>0$ (且 $b-ϵ>a$)，积分 ${\int }_a^{b-ϵ}f(x)dx$ 存在，并且极限
$$\underset{ϵ\to 0^{+}}{\lim }{\int }_a^{b-ϵ}f(x)dx$$
存在，则称此极限值为无界函数 $f(x)$ 在 $[a,b)$ 上的瑕积分，记作
$${\int }_a^{b}f(x)dx=\underset{ϵ\to 0^{+}}{\lim }{\int }_a^{b-ϵ}f(x)dx$$
若极限存在，称瑕积分 ${\int }_a^{b}f(x)dx$ 收敛；若极限不存在，称瑕积分发散。

③ 瑕点在积分区间的内部点 $c\in (a,b)$
设函数 $f(x)$ 在 $[a,c)$ 和 $(c,b]$ 上连续，但在 $x=c$ 处无界 (即 $c$ 为瑕点)。
如：${\int }_{-1}^1\frac{1}{x^2}dx$ (瑕点为 $x=0$)。

定义 3： 将积分在瑕点 $c$ 处拆开：
$${\int }_a^{b}f(x)dx={\int }_a^{c}f(x)dx+{\int }_c^{b}f(x)dx$$
其中 ${\int }_a^{c}f(x)dx={\lim }_{{ϵ}_1\to 0^{+}}{\int }_a^{c-{ϵ}_1}f(x)dx$ (瑕点在上限)
且 ${\int }_c^{b}f(x)dx={\lim }_{{ϵ}_2\to 0^{+}}{\int }_{c+{ϵ}_2}^{b}f(x)dx$ (瑕点在下限)。
如果右边的两个瑕积分 ${\int }_a^{c}f(x)dx$ 与 ${\int }_c^{b}f(x)dx$ 都收敛，则称瑕积分 ${\int }_a^{b}f(x)dx$ 收敛，其值为这两个收敛积分之和。如果其中至少有一个发散，则称瑕积分 ${\int }_a^{b}f(x)dx$ 发散。

④ 瑕点在积分区间的两端点 $a$ 和 $b$
设函数 $f(x)$ 在 $(a,b)$ 内连续，但在 $x=a$ 和 $x=b$ 处都无界 (即 $a,b$ 均为瑕点)。
如：${\int }_0^1\frac{1}{\sqrt{x(1-x)}}dx$ (瑕点为 $x=0$ 和 $x=1$)。
(原文示例 ${\int }_{-1}^1\frac{1}{x}dx$ 是内部瑕点，这里给一个两端瑕点的例子)

定义 4： 取积分区间 $(a,b)$ 内任意一点 $c$，将积分拆分：
$${\int }_a^{b}f(x)dx={\int }_a^{c}f(x)dx+{\int }_c^{b}f(x)dx$$
其中 ${\int }_a^{c}f(x)dx$ 是下限 $a$ 为瑕点的瑕积分，${\int }_c^{b}f(x)dx$ 是上限 $b$ 为瑕点的瑕积分。
如果右边的两个瑕积分 ${\int }_a^{c}f(x)dx$ 与 ${\int }_c^{b}f(x)dx$ 都收敛，则称瑕积分 ${\int }_a^{b}f(x)dx$ 收敛；如果其中至少有一个发散，则称瑕积分 ${\int }_a^{b}f(x)dx$ 发散。

---

例 1

判别下列广义积分的敛散性，若收敛，求其值：

$$(1){\int }_0^1\ln xdx(2){\int }_0^a\frac{1}{\sqrt{a^2-x^2}}dx(a>0)(3){\int }_{-1}^1\frac{1}{x^2}dx(4){\int }_{-1}^1\frac{x}{\sqrt{1-x^2}}dx$$

解：

(1) 瑕点是 $x=0$ (下限)。
$$\begin{array}{rl}{\int }_0^1\ln xdx& =\underset{ϵ\to 0^{+}}{\lim }{\int }_{ϵ}^1\ln xdx\\ \text{用分部积分法：}& u=\ln x,dv=dx\Rightarrow du=\frac{1}{x}dx,v=x\\ \int \ln xdx& =x\ln x-\int x\cdot \frac{1}{x}dx=x\ln x-x+C\\ \text{所以，}{\int }_0^1\ln xdx& =\underset{ϵ\to 0^{+}}{\lim }\left[x\ln x-x\right]{|}_{ϵ}^1\\ & =\underset{ϵ\to 0^{+}}{\lim }\left[(1\ln 1-1)-(ϵ\ln ϵ-ϵ)\right]\\ & =(0-1)-\underset{ϵ\to 0^{+}}{\lim }(ϵ\ln ϵ-ϵ)\\ \text{计算 }\underset{ϵ\to 0^{+}}{\lim }ϵ\ln ϵ:& \text{ 这是 }0\cdot (-\infty )\text{ 型，用洛必达法则}\\ \underset{ϵ\to 0^{+}}{\lim }ϵ\ln ϵ& =\underset{ϵ\to 0^{+}}{\lim }\frac{\ln ϵ}{1/ϵ}\stackrel{L^{\prime }H}{=}\underset{ϵ\to 0^{+}}{\lim }\frac{1/ϵ}{-1/{ϵ}^2}=\underset{ϵ\to 0^{+}}{\lim }(-ϵ)=0\\ \text{因此，}{\int }_0^1\ln xdx& =-1-(0-0)=-1\end{array}$$
所以该瑕积分收敛于 $-1$。
(注：瑕积分也可直接使用牛顿-莱布尼兹公式，但需将瑕点处的函数值理解为极限。即 ${(x\ln x-x)|}_0^1=(1\ln 1-1)-{\lim }_{x\to 0^{+}}(x\ln x-x)=-1$)

(2) 瑕点是 $x=a$ (上限)。
$$\begin{array}{rl}{\int }_0^a\frac{1}{\sqrt{a^2-x^2}}dx& =\underset{ϵ\to 0^{+}}{\lim }{\int }_0^{a-ϵ}\frac{1}{\sqrt{a^2-x^2}}dx\\ \text{我们知道 }\int \frac{1}{\sqrt{a^2-x^2}}dx& =\arcsin \frac{x}{a}+C\\ \text{所以，}{\int }_0^a\frac{1}{\sqrt{a^2-x^2}}dx& =\underset{ϵ\to 0^{+}}{\lim }\left[\arcsin \frac{x}{a}\right]{|}_0^{a-ϵ}\\ & =\underset{ϵ\to 0^{+}}{\lim }\left(\arcsin \frac{a-ϵ}{a}-\arcsin \frac{0}{a}\right)\\ & =\arcsin (1)-\arcsin (0)\\ & =\frac{\pi }{2}-0=\frac{\pi }{2}\end{array}$$
所以该瑕积分收敛于 $\frac{\pi }{2}$。
(也可令 $x=a\sin t$, $dx=a\cos tdt$。当 $x=0,t=0$。当 $x\to a^{-},t\to \pi /2^{-}$。
${\int }_0^{\pi /2}\frac{a\cos tdt}{\sqrt{a^2-a^2{\sin }^{2}t}}={\int }_0^{\pi /2}\frac{a\cos tdt}{a\cos t}={\int }_0^{\pi /2}1dt={t|}_0^{\pi /2}=\frac{\pi }{2}$)

(3) 瑕点是 $x=0$ (内部点)。
$${\int }_{-1}^1\frac{1}{x^2}dx={\int }_{-1}^0\frac{1}{x^2}dx+{\int }_0^1\frac{1}{x^2}dx$$
计算第一部分：${\int }_{-1}^0\frac{1}{x^2}dx={\lim }_{ϵ\to 0^{+}}{\int }_{-1}^{0-ϵ}\frac{1}{x^2}dx$
$$\begin{array}{rl}\underset{ϵ\to 0^{+}}{\lim }{\int }_{-1}^{-ϵ}{x}^{-2}dx& =\underset{ϵ\to 0^{+}}{\lim }\left[\frac{x^{-1}}{-1}\right]{|}_{-1}^{-ϵ}\\ & =\underset{ϵ\to 0^{+}}{\lim }\left[-\frac{1}{x}\right]{|}_{-1}^{-ϵ}\\ & =\underset{ϵ\to 0^{+}}{\lim }\left(-\frac{1}{-ϵ}-\left(-\frac{1}{-1}\right)\right)\\ & =\underset{ϵ\to 0^{+}}{\lim }\left(\frac{1}{ϵ}-1\right)=+\infty \end{array}$$
由于 ${\int }_{-1}^0\frac{1}{x^2}dx$ 发散，所以原瑕积分 ${\int }_{-1}^1\frac{1}{x^2}dx$ 发散。(无需计算第二部分)

(4) 瑕点是 $x=-1$ (下限) 和 $x=1$ (上限)。被积函数 $f(x)=\frac{x}{\sqrt{1-x^2}}$。
我们可以选择 $c=0$ 作为分割点：
$${\int }_{-1}^1\frac{x}{\sqrt{1-x^2}}dx={\int }_{-1}^0\frac{x}{\sqrt{1-x^2}}dx+{\int }_0^1\frac{x}{\sqrt{1-x^2}}dx$$
计算 $\int \frac{x}{\sqrt{1-x^2}}dx$：令 $u=1-x^2$, $du=-2xdx\Rightarrow xdx=-\frac{1}{2}du$。
$\int \frac{-\frac{1}{2}du}{\sqrt{u}}=-\frac{1}{2}\int u^{-1/2}du=-\frac{1}{2}\frac{u^{1/2}}{1/2}=-\sqrt{u}=-\sqrt{1-x^2}$。

第一部分：
$$\begin{array}{rl}{\int }_{-1}^0\frac{x}{\sqrt{1-x^2}}dx& =\underset{ϵ\to 0^{+}}{\lim }{\int }_{-1+ϵ}^0\frac{x}{\sqrt{1-x^2}}dx\\ & =\underset{ϵ\to 0^{+}}{\lim }\left[-\sqrt{1-x^2}\right]{|}_{-1+ϵ}^0\\ & =\underset{ϵ\to 0^{+}}{\lim }\left(-\sqrt{1-0^2}-(-\sqrt{1-(-1+ϵ{)}^2})\right)\\ & =-1-\underset{ϵ\to 0^{+}}{\lim }(-\sqrt{1-(1-2ϵ+{ϵ}^2)})\\ & =-1-\underset{ϵ\to 0^{+}}{\lim }(-\sqrt{2ϵ-{ϵ}^2})=-1-0=-1\text{(收敛)}\end{array}$$
第二部分：
$$\begin{array}{rl}{\int }_0^1\frac{x}{\sqrt{1-x^2}}dx& =\underset{\delta \to 0^{+}}{\lim }{\int }_0^{1-\delta }\frac{x}{\sqrt{1-x^2}}dx\\ & =\underset{\delta \to 0^{+}}{\lim }\left[-\sqrt{1-x^2}\right]{|}_0^{1-\delta }\\ & =\underset{\delta \to 0^{+}}{\lim }\left(-\sqrt{1-(1-\delta {)}^2}-(-\sqrt{1-0^2})\right)\\ & =\underset{\delta \to 0^{+}}{\lim }(-\sqrt{1-(1-2\delta +{\delta }^2)})+1\\ & =\underset{\delta \to 0^{+}}{\lim }(-\sqrt{2\delta -{\delta }^2})+1=0+1=1\text{(收敛)}\end{array}$$
因为两部分都收敛，所以原瑕积分收敛，其值为 $-1+1=0$。
(注：此题中被积函数 $f(x)=\frac{x}{\sqrt{1-x^2}}$ 是奇函数，积分区间 $[-1,1]$ 关于原点对称。由于两边分别收敛，可以利用奇函数的性质得到结果为0。但必须先验证各自收敛。)

---

例 2 (q-积分)

证明瑕积分 ${\int }_0^1\frac{1}{x^q}dx$ (瑕点为 $x=0$)：

• 当 $0<q<1$ 时收敛，其值为 $\frac{1}{1-q}$。
• 当 $q\ge 1$ 时发散。

证明：

(1) 当 $q=1$ 时：
$${\int }_0^1\frac{1}{x^q}dx={\int }_0^1\frac{1}{x}dx=\underset{ϵ\to 0^{+}}{\lim }{\int }_{ϵ}^1\frac{1}{x}dx=\underset{ϵ\to 0^{+}}{\lim }\left[\ln x\right]{|}_{ϵ}^1=\underset{ϵ\to 0^{+}}{\lim }(\ln 1-\ln ϵ)=0-(-\infty )=+\infty$$
所以当 $q=1$ 时，积分发散。

(2) 当 $q\ne 1$ 时：
$$\begin{array}{rl}{\int }_0^1\frac{1}{x^q}dx& ={\int }_0^1{x}^{-q}dx\\ & =\underset{ϵ\to 0^{+}}{\lim }\left[\frac{x^{-q+1}}{-q+1}\right]{|}_{ϵ}^1\\ & =\frac{1}{1-q}\underset{ϵ\to 0^{+}}{\lim }\left(1^{1-q}-{ϵ}^{1-q}\right)\\ & =\frac{1}{1-q}\left(1-\underset{ϵ\to 0^{+}}{\lim }{ϵ}^{1-q}\right)\end{array}$$
现在需要讨论 $1-q$ 的符号：

• 若 $0<q<1$ (即 $q<1$)，则 $1-q>0$。此时 ${\lim }_{ϵ\to 0^{+}}{ϵ}^{1-q}=0$。
  所以积分为 $\frac{1}{1-q}(1-0)=\frac{1}{1-q}$。积分收敛。
• 若 $q>1$，则 $1-q<0$。此时 ${\lim }_{ϵ\to 0^{+}}{ϵ}^{1-q}={\lim }_{ϵ\to 0^{+}}\frac{1}{{ϵ}^{q-1}}=+\infty$。
  所以积分为 $\frac{1}{1-q}(1-\infty )=+\infty$ (因为 $1-q<0$，所以 $\frac{1}{1-q}$ 是负数，乘以 $-\infty$ 得到 $+\infty$)。积分发散。

综合 (1) 和 (2) 可知：
瑕积分 ${\int }_0^1\frac{1}{x^q}dx$ (瑕点 $x=0$) 当 $0<q<1$ 时收敛 (值为 $\frac{1}{1-q}$)，当 $q\ge 1$ 时发散。
(通常这个结论也适用于瑕点在上限 $b$ 的情况，如 ${\int }_a^b\frac{1}{(b-x{)}^q}dx$ 等价于 ${\int }_0^{b-a}\frac{1}{y^q}dy$ 作代换 $y=b-x$)

---

例 3

计算广义积分：
$${\int }_0^{+\infty }\frac{dx}{\sqrt{x(x+1{)}^3}}$$

解：
该积分既是无穷限积分 (上限为 $+\infty$)，又是瑕积分 (下限 $x=0$ 是瑕点)。
我们选择一个中间点，例如 $c=1$，将积分拆分：
$$I={\int }_0^{+\infty }\frac{dx}{\sqrt{x(x+1{)}^3}}={\int }_0^1\frac{dx}{\sqrt{x(x+1{)}^3}}+{\int }_1^{+\infty }\frac{dx}{\sqrt{x(x+1{)}^3}}=I_1+I_2$$
先计算不定积分 $\int \frac{dx}{\sqrt{x(x+1{)}^3}}$。
令 $\sqrt{x}=t$，则 $x=t^2$，$dx=2tdt$。
$$\int \frac{2tdt}{\sqrt{t^2(t^2+1{)}^3}}=\int \frac{2tdt}{t(t^2+1{)}^{3/2}}=2\int \frac{dt}{(t^2+1{)}^{3/2}}$$
再令 $t=\tan u$，则 $dt={\sec }^{2}udu$，$t^2+1={\tan }^{2}u+1={\sec }^{2}u$。
$$2\int \frac{{\sec }^{2}udu}{({\sec }^{2}u{)}^{3/2}}=2\int \frac{{\sec }^{2}udu}{{\sec }^{3}u}=2\int \frac{1}{\sec u}du=2\int \cos udu=2\sin u+C$$
将 $u$ 换回 $t$：因为 $\tan u=t$, 所以 $\sin u=\frac{t}{\sqrt{t^2+1}}$ (画直角三角形可知)。
所以不定积分为 $2\frac{t}{\sqrt{t^2+1}}+C=2\frac{\sqrt{x}}{\sqrt{x+1}}+C=2\sqrt{\frac{x}{x+1}}+C$。

现在计算 $I_1$ 和 $I_2$：
$I_1$ (瑕积分，瑕点 $x=0$)：
$$\begin{array}{rl}{I}_1={\int }_0^1\frac{dx}{\sqrt{x(x+1{)}^3}}& =\left[2\sqrt{\frac{x}{x+1}}\right]{|}_0^1\\ & =2\sqrt{\frac{1}{1+1}}-\underset{x\to 0^{+}}{\lim }2\sqrt{\frac{x}{x+1}}\\ & =2\sqrt{\frac{1}{2}}-2\sqrt{0}=2\frac{1}{\sqrt{2}}-0=\sqrt{2}\text{(收敛)}\end{array}$$
$I_2$ (无穷限积分)：
$$\begin{array}{rl}{I}_2={\int }_1^{+\infty }\frac{dx}{\sqrt{x(x+1{)}^3}}& =\left[2\sqrt{\frac{x}{x+1}}\right]{|}_1^{+\infty }\\ & =\underset{x\to +\infty }{\lim }2\sqrt{\frac{x}{x+1}}-2\sqrt{\frac{1}{1+1}}\\ & =\underset{x\to +\infty }{\lim }2\sqrt{\frac{1}{1+1/x}}-2\sqrt{\frac{1}{2}}\\ & =2\sqrt{1}-\sqrt{2}=2-\sqrt{2}\text{(收敛)}\end{array}$$
因为 $I_1$ 和 $I_2$ 都收敛，所以原积分 $I$ 收敛，其值为：
$I=I_1+I_2=\sqrt{2}+(2-\sqrt{2})=2$。

---

总结

1. 反常积分的分类：

   • 无穷限积分： 积分区间为无限，如 ${\int }_a^{+\infty }f(x)dx$, ${\int }_{-\infty }^{b}f(x)dx$, ${\int }_{-\infty }^{+\infty }f(x)dx$。
   • 瑕积分： 积分区间有限，但被积函数在区间内有无界点 (瑕点)。

2. 定义与计算：

   • 所有反常积分都通过极限来定义。
   • ${\int }_a^{+\infty }f(x)dx={\lim }_{t\to +\infty }{\int }_a^{t}f(x)dx$。
   • ${\int }_a^{b}f(x)dx$ (若 $a$ 为瑕点) $={\lim }_{ϵ\to 0^{+}}{\int }_{a+ϵ}^{b}f(x)dx$。
   • 若积分涉及多个反常点 (如 ${\int }_{-\infty }^{+\infty }$ 或内部瑕点)，需要拆分积分，确保每一部分都独立收敛，则总积分收敛。

3. 重要的判别模型：

   • p-积分 (无穷限)： ${\int }_1^{+\infty }\frac{1}{x^p}dx$ 当 $p>1$ 时收敛，当 $p\le 1$ 时发散。
   • q-积分 (瑕积分，瑕点在0)： ${\int }_0^1\frac{1}{x^q}dx$ 当 $0<q<1$ 时收敛，当 $q\ge 1$ 时发散。 (一般地，${\int }_a^b\frac{dx}{(x-a{)}^q}$ 或 ${\int }_a^b\frac{dx}{(b-x{)}^q}$ 敛散性同 ${\int }_0^c\frac{dx}{x^q}$)

4. 计算技巧：

   • 计算反常积分时，先按不定积分或正常定积分的方法求出原函数。
   • 然后代入积分限，遇到 $\infty$ 或瑕点时，实质上是求相应的极限。
   • 换元法、分部积分法等正常积分的计算方法同样适用于反常积分的计算过程。

5. 敛散性判断：

   • 在计算前，首先要判断积分类型（无穷限、瑕积分，或两者皆是）。
   • 识别瑕点的位置。
   • 严格按照定义处理极限，或利用已知的判别模型。