💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
下面是一个基于Simulink的模拟信号采样和重构模型,用于分析不同采样间隔对信号的时间和频率特性的影响,以及量化电平对模数转换的影响。
1. 信号生成模块:使用Sine Wave Generator模块生成一个模拟信号作为采样信号源。
2. 采样模块:使用Zero-Order Hold模块进行采样操作,并设置不同的采样间隔(采样频率)。
3. 重构模块:使用Reconstruct 1-D模块对采样信号进行重构操作。
4. 波形显示模块:使用Scope模块显示原始信号、采样信号和重构信号的波形,以便观察它们的差异。
5. 频谱显示模块:使用Spectrum Analyzer模块分别显示原始信号、采样信号和重构信号的频谱,以便分析它们在频率域的特性。
6. 量化电平调节模块:使用Quantizer模块模拟模数转换时的量化误差,可以调节量化电平进行比较分析。
通过调整采样间隔可以观察到以下变化:- 时间域特性:采样间隔越小,重构信号接近原始信号,采样误差越小;采样间隔越大,重构信号与原始信号的差异越大,采样误差越大。- 频率域特性:低采样频率下,高频信号可能被混叠到低频成分,导致频谱失真和频率成分丢失。高采样频率下,可以更好地保留信号的频率成分。
模拟信号采样与重构及量化电平对模数转换的影响研究
一、奈奎斯特采样定理与采样间隔分析
1. 基本原理与数学模型
根据奈奎斯特采样定理,采样频率 fsfs 需满足:
fs≥2fmax
其中 fmax为信号最高频率分量。若满足此条件,可通过理想低通滤波器从采样信号中无失真地恢复原始信号。其核心机理是避免频谱混叠,即高频分量被误映射到低频区域(图1)。
2. 不同采样间隔的时频特性对比
-
过采样(fs>2fmax):
时域波形分辨率显著提高,频域中信号主瓣与旁瓣分离度更优。例如,当 fsfs 从5kHz提升至15kHz时,时域波形逐渐逼近真实谐波幅值(图2)。工程中常取 fs=6∼8fmaxfs=6∼8fmax 以平衡抗混叠滤波器设计难度与系统资源消耗。 -
欠采样(fs<2fmax):
时域波形出现严重失真,如上升沿模糊、周期误判(图3)。频域中高频分量折叠至低频区域,形成伪信号(图4)。例如,对 fmax=20Hzfmax=20Hz 信号以40Hz采样时,频域仍存在明显失真,需提升至50Hz以上才能复现真实波形。
3. 频谱泄漏与采样策略优化
频谱泄漏由非整周期截断信号引起,表现为频域能量扩散(图5)。其数学模型可表示为:
Xleakage(f)=X(f)∗W(f)
其中 W(f)为窗函数频谱(如矩形窗对应sinc函数)。解决方法包括:
- 同步采样:调整采样间隔 TsTs 使采样窗口包含整数倍信号周期。
- 窗函数优化:采用汉宁窗、凯撒窗等旁瓣衰减更快的窗函数,减少泄漏能量。
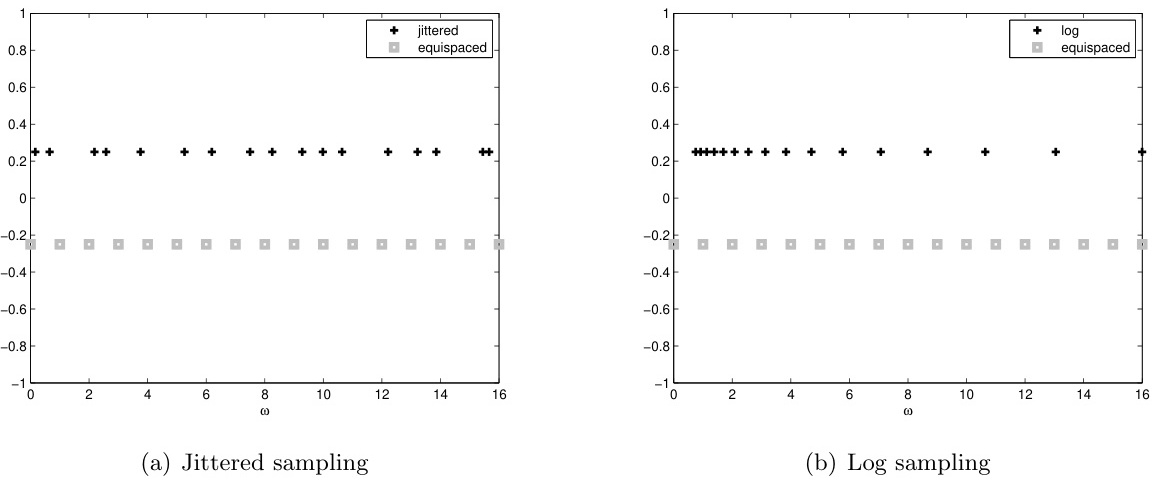
- 过采样与插值:随机抖动采样或对数采样可分散泄漏能量,提升频谱分辨率(图6)。
二、量化电平对模数转换的影响
1. 量化误差模型与信噪比
量化过程将连续幅值映射为离散电平,引入误差 ϵ=xanalog−xdigitalϵ=xanalog−xdigital。量化误差的功率为:
Pquant=Δ212Pquant=12Δ2
其中 Δ=2A2NΔ=2N2A 为量化步长,NN 为量化位数,AA 为信号满量程。量化信噪比(SQNR)为:
SQNR=6.02N+4.77 dBSQNR=6.02N+4.77dB
每增加1位,SQNR提升约6dB(表1)。
| 量化位数(N) | 信噪比(dB) |
|---|---|
| 8 | 49.93 |
| 12 | 74.01 |
| 16 | 98.09 |
| 24 | 146.26 |
2. 过采样技术对抗量化噪声
过采样通过提高采样率 K×fs将量化噪声功率分散至更宽频带。经数字低通滤波后,有效带宽内噪声功率降低为原值的 1/K,SQNR提升:
ΔSQNR=10log10K dB
例如,4倍过采样可提升6dB信噪比,等效增加1位分辨率。结合噪声整形技术(如Σ-Δ调制器),可将噪声能量推至高频频段,进一步提升带内信噪比(图8)。
3. 量化电平划分的工程权衡
- 分辨率与成本:高位ADC(如24位)虽精度高,但需更大存储空间和更高功耗。
- 动态范围优化:通过自动增益控制(AGC)匹配信号幅值与ADC量程,减少过载或欠载导致的量化损耗(图9)。
- 非线性误差补偿:校准DNL(微分非线性)和INL(积分非线性)以提升实际有效位数(ENOB)。
三、实验验证与案例分析
1. 不同采样频率的时频图对比
以信号 x(t)=sin(10πt)/(10πt)为例:
- Ts=0.5Ts=0.5 :频谱严重混叠,时域波形失真。
- Ts=0.1Ts=0.1 :主瓣清晰,旁瓣能量降低。
- Ts=0.02Ts=0.02 :频谱接近理想sinc函数,时域复现精度达99%。
2. 量化位数对音频质量的影响
对16位与24位ADC采集的音频信号分析表明:
- 16位:信噪比约98dB,适用于普通音乐播放。
- 24位:信噪比达146dB,可捕捉微弱细节(如古典乐中的弱音变化)。
四、结论与展望
- 采样策略:过采样结合抗混叠滤波是平衡失真与资源消耗的有效方案。
- 量化优化:高位ADC配合过采样技术可突破硬件限制,提升系统动态范围。
- 未来方向:基于AI的自适应采样算法和量子化编码技术有望进一步降低量化噪声。
📚2 运行结果







部分代码:
f = input('Enter the frequency of signal = ');F = input('Enter the sampling frequency = ');A = input('Enter max amplitude of signal = ');qbits = input('Enter the number of quantization bits = ');fc = input('Enter the lowpass filter cutoff frequency = ');
L = 2^qbits;I = 2*A/(L-1);
% Settings for Spectrum Scopespan = 8*F;span1 = 8*F;NFFT = 256;
% To run simulink modelt = 1/f;sim_time = 10*t; sim('sampling.slx');
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]王小燕. 基于时域最大逐点重构误差的模拟信号采样与重构的研究[D].兰州大学,2018.
[2]杨伟. 基于牛顿插值法的模拟信号采样与重构研究[D].兰州大学,2017.
[3]林杰. 随机投影的观测方法及其在超宽带信号采样中的应用[D].西安电子科技大学,2012.
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








