欠驱动动态稳定的单球轮移动机器人（Ballbot）轨迹规划与控制研究（Matlab代码实现）-CSDN博客

本文链接：https://blog.csdn.net/2302_77323582/article/details/147362481

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

⛳️赠与读者

💥1 概述

欠驱动动态稳定的单球轮移动机器人（Ballbot）轨迹规划与控制研究

1. Ballbot的基本结构与动态特性

2. 欠驱动系统的动态约束与控制挑战

3. 离线轨迹规划算法设计

4. 反馈控制器设计原理

5. 非静态配置运动的数学建模扩展

6. 实验验证与性能分析

7. 结论与展望

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能解答你胸中升起的一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

欠驱动动态稳定的单球轮移动机器人（Ballbot）轨迹规划与控制研究

摘要：
Ballbot是一种动态稳定的移动机器人，它通过一个单球轮移动，并能够实现全方位运动。Ballbot是一个具有非完整动态约束的欠驱动系统。作者提出了一种离线轨迹规划算法，该算法为未驱动关节提供了一类参数化轨迹，以便在动态约束下使系统达到期望的静态配置。轨迹的参数是通过优化技术获得的。此外，作者还提出了一种反馈控制器，以确保精确的轨迹跟踪。通过实验验证了轨迹规划算法和跟踪控制器的有效性。作者还将离线轨迹规划算法扩展到非静态配置之间的运动的更一般情况。

关键词：
执行器、反馈、移动机器人、优化、路径规划、机器人动力学、稳定性、轨迹跟踪、Ballbot、欠驱动、动态稳定、单球轮移动机器人、反馈控制器

1. Ballbot的基本结构与动态特性

Ballbot是一种通过单球轮实现全方位运动的动态稳定机器人。其核心结构由三部分组成（图1）：

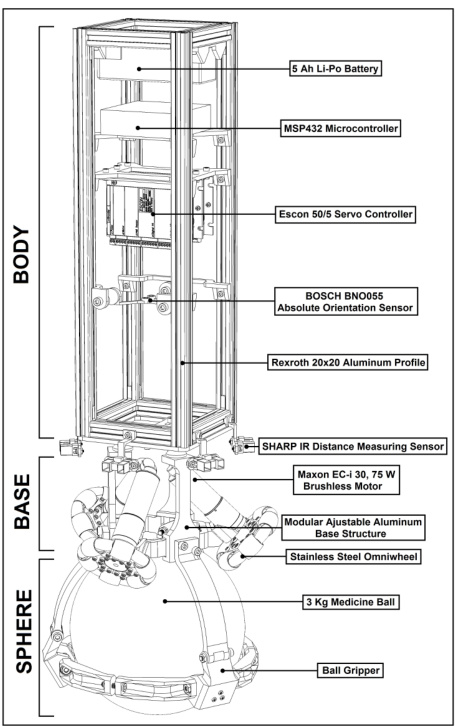
身体部分：包含电池（5 Ah锂聚合物电池）、微控制器（MSP432）、伺服控制器（Escon 50/6）、惯性测量单元（BOSCH BNO055）及支撑结构（Rexroth铝型材）。
基座部分：采用Maxon EC-i 30无刷电机驱动球体，搭配可调铝制基座和不锈钢万向轮，确保灵活运动。
球体部分：3公斤药球作为驱动核心，表面覆有聚氨酯涂层以增强摩擦力。

其动态特性表现为高重心（约1.41米）和小支撑面（直径0.37米），需通过主动控制维持平衡。与传统轮式机器人不同，Ballbot具有二阶非完整约束，即运动方向与驱动方向非直接耦合，需通过倾斜身体产生力矩驱动球体。

2. 欠驱动系统的动态约束与控制挑战

欠驱动系统的控制输入维度小于自由度维度，导致以下特性：

非完整约束：无法通过局部控制直接调节所有自由度，需依赖动态耦合效应。例如，Ballbot需通过倾斜角度间接控制水平位移。
非最小相位特性：零动态（未被直接控制的自由度）可能不稳定，需通过轨迹规划与反馈控制协同稳定。
优化复杂度：轨迹参数需满足动力学方程与约束条件，需结合数值优化技术（如遗传算法、粒子群优化）求解。

3. 离线轨迹规划算法设计

作者提出的离线轨迹规划算法核心步骤如下：

参数化轨迹生成：为未驱动关节设计参数化轨迹，例如多项式曲线或S形曲线，确保满足非完整约束。
多目标优化：以能量最小、时间最短或路径平滑为目标，通过遗传算法或差分进化算法优化轨迹参数。例如，针对垂直三连杆欠驱动系统，采用时间缩放法生成双向轨迹，并通过优化中间点实现拼接。
扩展至非静态配置：将静态平衡点间的轨迹规划推广到动态运动场景，通过动态模型预测（如Bishop参数化）调整轨迹参数，适应连续位姿变化。

4. 反馈控制器设计原理

为确保轨迹跟踪精度，作者设计了分层反馈控制器：

内环平衡控制：采用状态反馈或滑模控制，实时调整身体倾斜角以维持动态平衡。例如，基于李雅普诺夫稳定性理论设计控制律，通过极点配置优化响应速度。
外环轨迹跟踪：结合前馈与反馈控制，前馈部分基于离线轨迹生成期望力矩，反馈部分（如PID或LQR）补偿模型误差和扰动。实验表明，PID-LQR组合控制器可将倾斜角误差控制在3°以内，轨迹跟踪偏差小于2°。

5. 非静态配置运动的数学建模扩展

针对动态环境中的连续运动，算法扩展涉及：

动态状态估计：采用扩展卡尔曼滤波（EKF）融合IMU数据，实时更新位姿与速度。
轨迹重规划：基于随机矩阵或变分扩展方法，建立机动目标的状态-形态联合模型，通过贝叶斯估计优化轨迹参数。
多模态切换优化：分阶段设计轨迹，将不同运动模态（如加速、转向）的切换状态作为优化变量，实现平滑过渡。

6. 实验验证与性能分析

实验体系通过仿真与实物测试验证算法有效性：

平衡能力：在干扰力达204 N时仍能保持稳定，倾斜角波动小于3°。
轨迹跟踪：全向移动的航向偏差控制在2°内，最大速度达1.9 m/s。
鲁棒性：分层滑模控制器在外部扰动下表现出强鲁棒性，仿真与实物结果一致。

7. 结论与展望

本研究通过参数化轨迹规划与分层反馈控制，解决了Ballbot的欠驱动与非完整约束问题，并成功扩展至动态运动场景。未来方向包括：

传感器融合：集成激光雷达与视觉SLAM，提升复杂环境下的轨迹适应性。
能源优化：改进电机效率（如球形感应电机），降低功耗。
人机交互：利用动态稳定性实现安全物理交互，拓展服务机器人应用场景。

通过理论创新与实验验证，Ballbot在狭窄空间导航、载重运输等领域展现出潜力，为欠驱动系统控制提供了重要参考。

📚2 运行结果

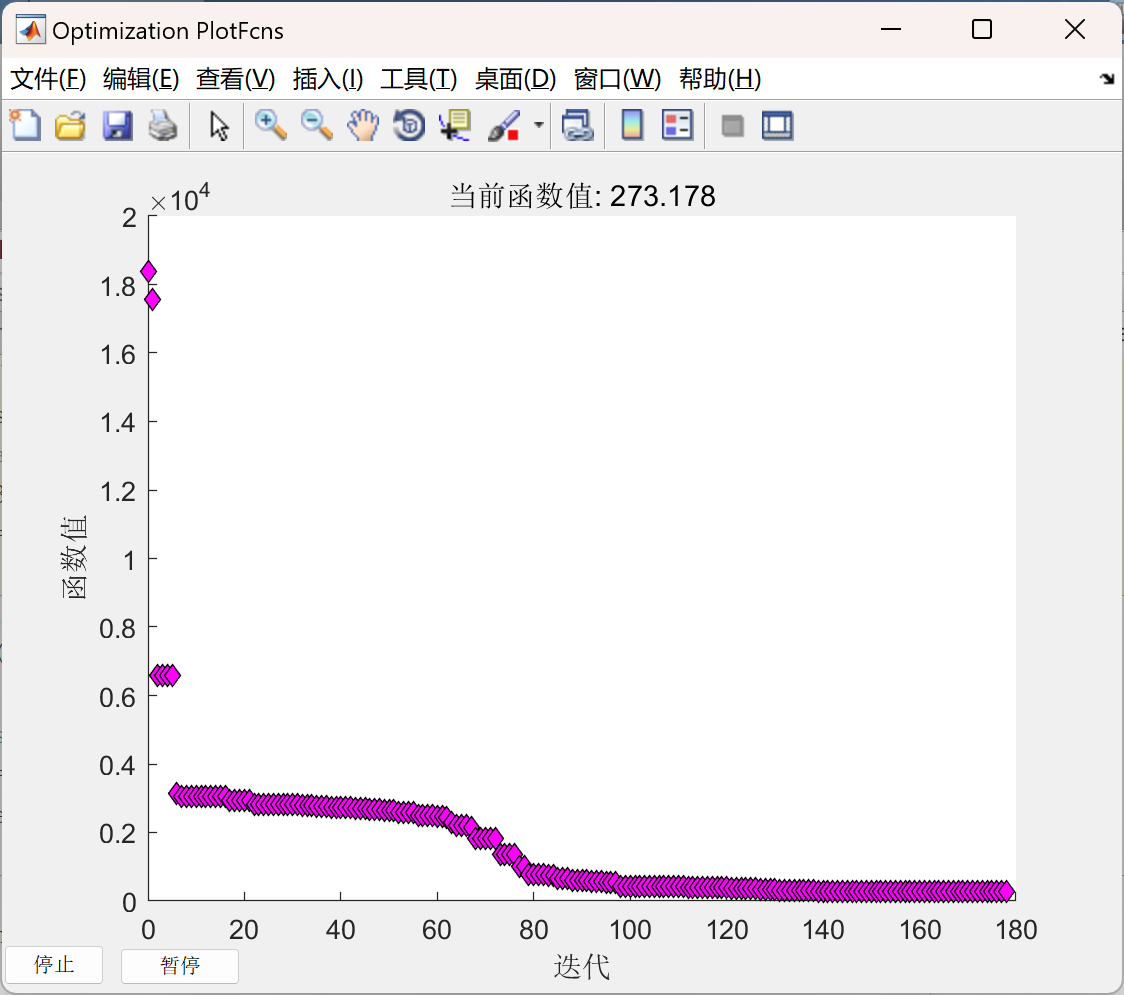
部分代码：

%% load ballbot parameters and set initial and final desired states
clearvars;
run('parameters.m');
x0 = [0.35;-0.35;15];
thetadf = 1/rw;

%% optimization
func = @(x) cost_function(x,alp,bet,gam,g,rw,Dc,Dv,thetadf);

% options = optimset('Display','iter','PlotFcns',@optimplotfval);
options = optimset('Display','iter');
[x,fval,exitflag] = fminsearch(func,x0,options);

%% visualize results
[t,phi,phid,times,THETA,tau] = get_trajs(x,alp,bet,gam,g,rw,Dc,Dv);
phival = double(subs(phi,t,times));
phidval = double(subs(phid,t,times));

render([THETA(:,1) phival],times,rw);
plot_the_plots(times,THETA,phival,phidval,tau,rw);