第十五届蓝桥杯C/C++B组题解——R格式

题目描述

小蓝最近在研究一种浮点数的表示方法：R 格式。对于一个大于 0 的浮点数 d，可以用 R 格式的整数来表示。给定一个转换参数 n，将浮点数转换为 R格式整数的做法是：

1. 将浮点数乘以 2^n;

2. 四舍五入到最接近的整数。

输入格式

一行输入一个整数 n 和一个浮点数 d，分别表示转换参数，和待转换的浮点数。

输出格式

输出一行表示答案：d 用 R 格式表示出来的值。

样例输入

2 3.14

样例输出

13

提示

【样例说明】

3.14 × 22 = 12.56，四舍五入后为 13。

【评测用例规模与约定】

对于 50% 的评测用例：1 ≤ n ≤ 10，1 ≤ 将 d 视为字符串时的长度 ≤ 15。

对于 100% 的评测用例：1 ≤ n ≤ 1000，1 ≤ 将 d 视为字符串时的长度≤ 1024；保证 d 是小数，即包含小数点。

题目分析

对于50%的用例，直接开double，不是问题，但对于100%的用例，便需要使用高精度算法对浮点数进行模拟运算，下面结合图片一起分析。先用字符串变量，将数据存储起来，然后反向存储在数组中。

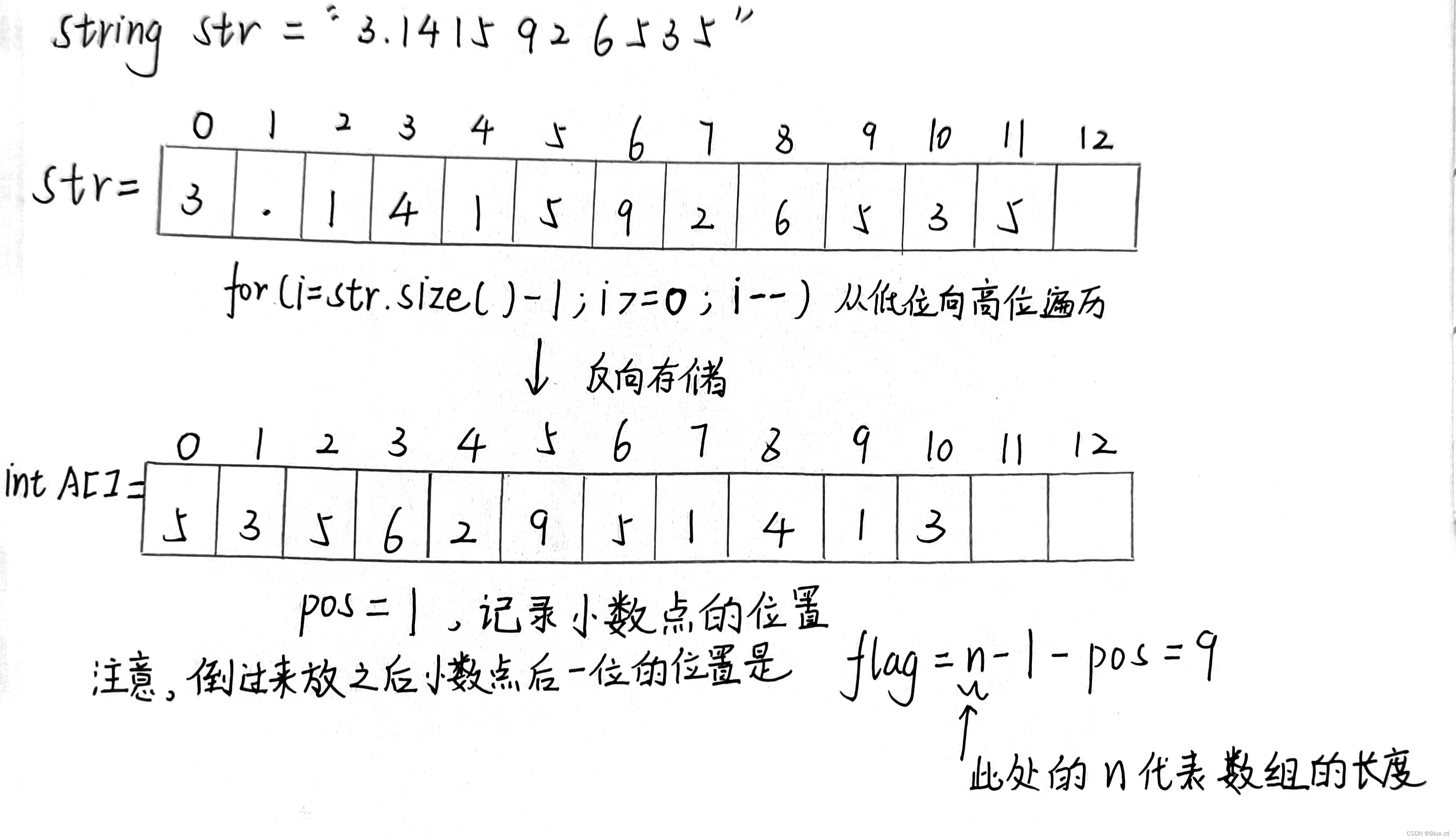
为什么在此处，我们选择倒过来存储呢？答案是，方便进位。

如果正着放，最高位有进位的话，那就超出了数组的范围。

接着分析，本题是欲将一个浮点数乘上2^n，那么问题就可以转换成，将数组A[]，每一位都乘上2然后，模拟进位的过程。

多说无益，此处我们对3.1415926535，这个数乘上2^3，进行模拟，请读者仔细阅读。

在这里我用t来代表来自低位的进位

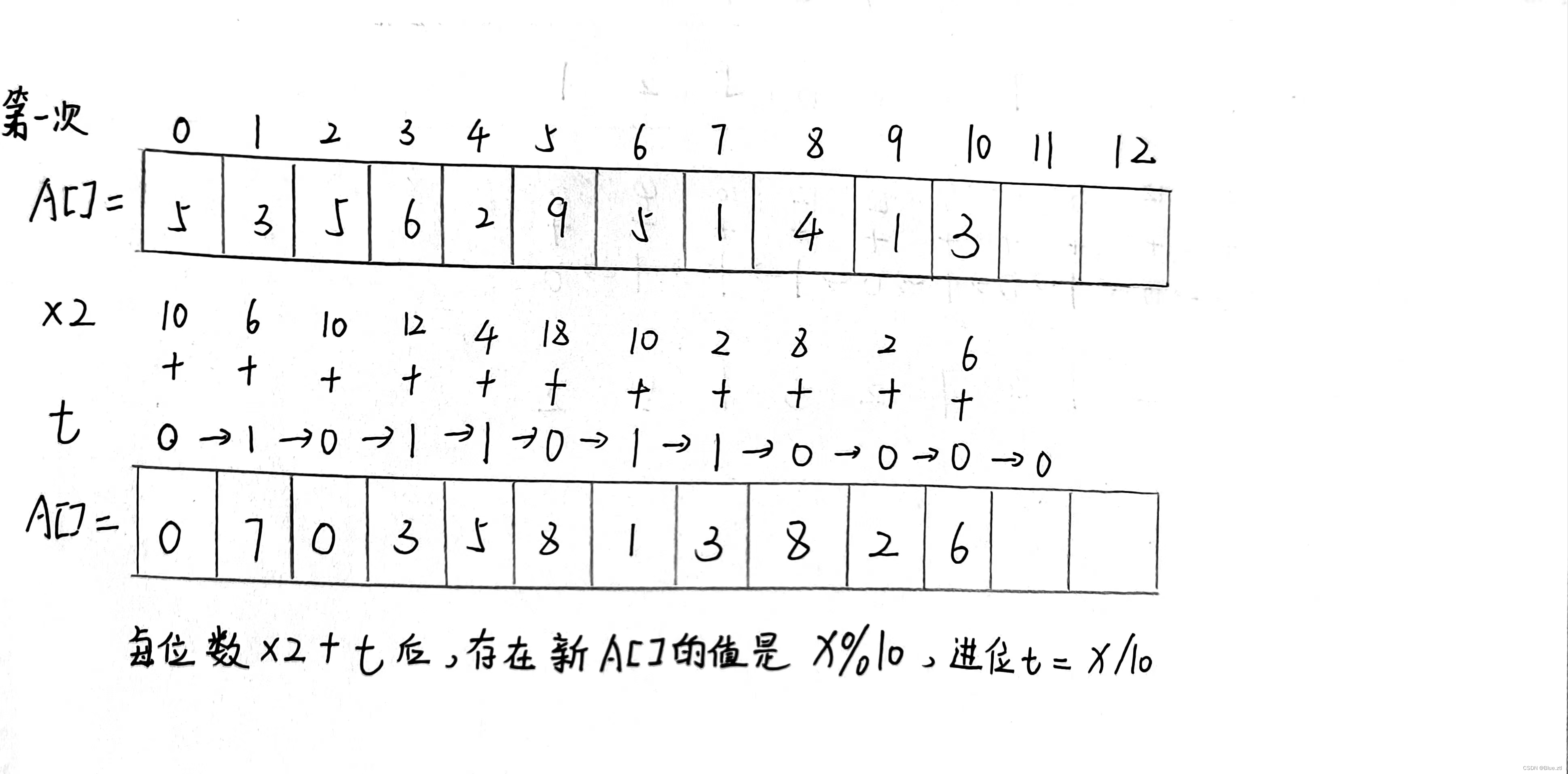
t=0;
for(int i=0;i<j;i++)
{
	int x=A[i]*2+t;
	t=x/10;
	A[i]=x%10;
}

此过程可以，写成这样的代码，注意在此处，j是数组A的长度。 

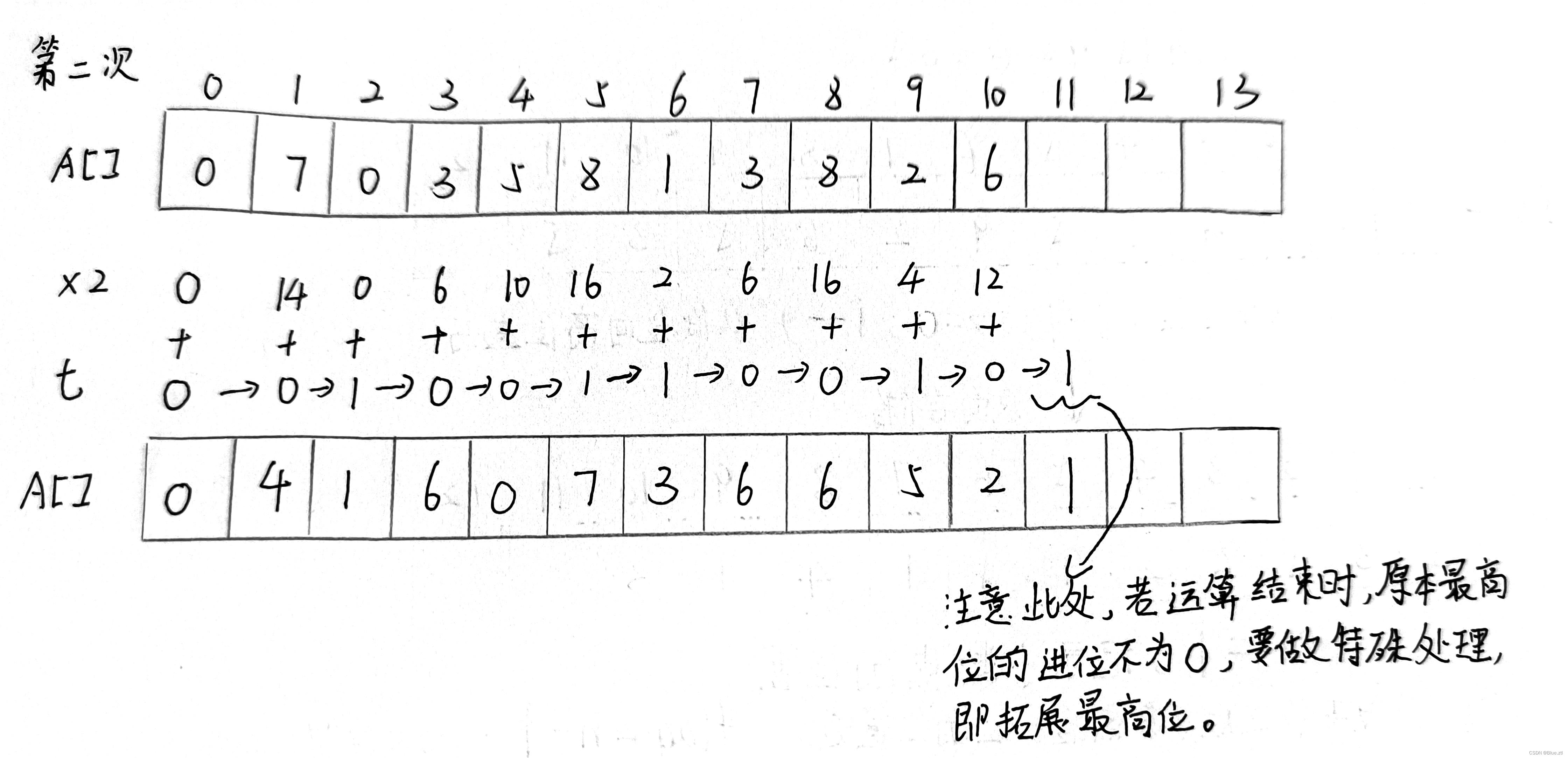
第二次，我们发现运算结束时，最高位的进位不为0，那我们就要扩展最高位，代码是这样写。

	t=0;
	for(int i=0;i<j;i++)
	{
		int x=A[i]*2+t;
		t=x/10;
		A[i]=x%10;
	}
	if(t==1)
	{
		A[j++]=t;
	}

 第三次

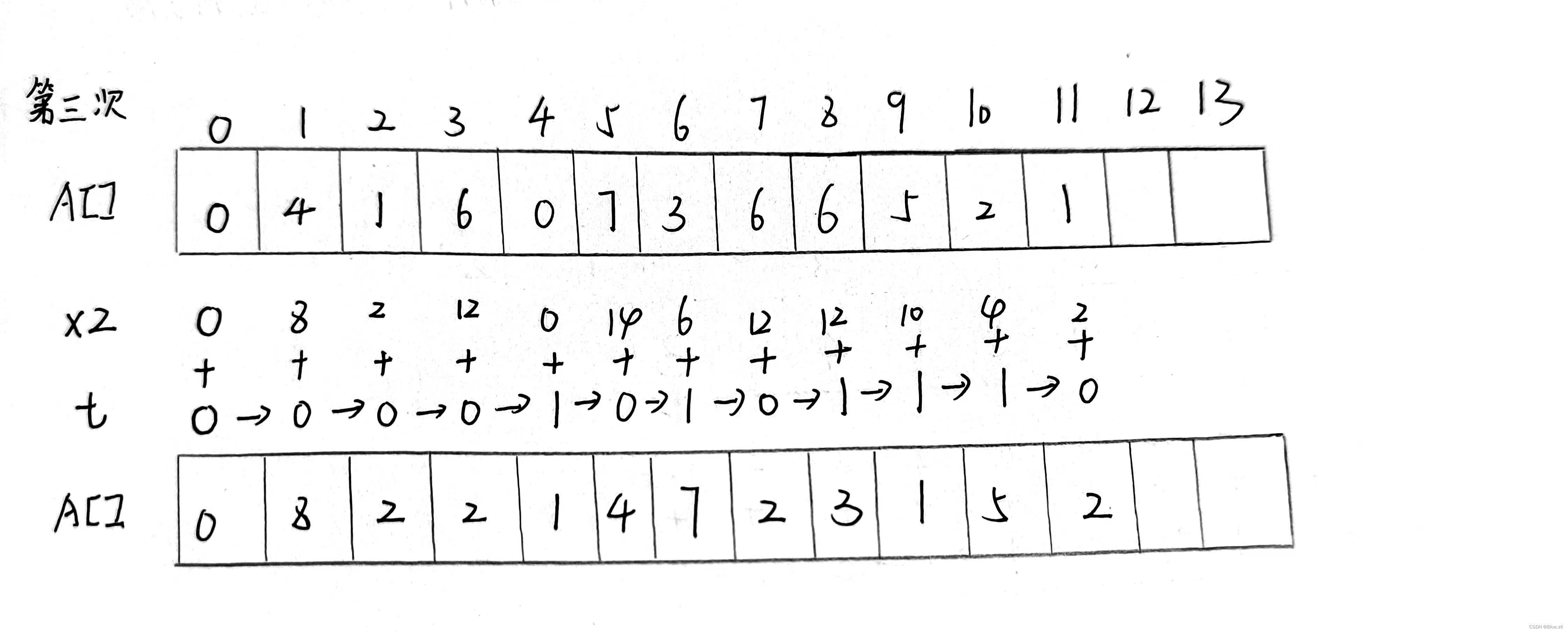
到此三次模拟全部结束，接下来我们要做的便是四舍五入，我们数据是倒着存在数组A中的，前面我们已经计算出小数点后一位的位置flag。那么如果A[flag]>=5,那低位进位t=1，进行一次模拟，否则就直接输出整数部分即可。 

下面给出AC代码

#include <iostream>
#include <string>
using namespace std; 
const int N=1e5+10;
int A[N];
string str;//字符串，存储浮点数 
int n,j;//n是字符串的长度，j是按数组存储后数组的长度 
int pos,flag,t;//pos是小数点原来在字符串中出现的位置,t是来自低位的进位 
void fun()
{
	while(n--)
	{
		t=0;
		for(int i=0;i<j;i++)
		{
			int x=A[i]*2+t;
			t=x/10;
			A[i]=x%10;
		}
		if(t==1)
		{
			A[j++]=t;
		}
	}
}
int main()
{
	cin>>n;
	cin>>str;
	j=0;
	for(int i=str.size()-1;i>=0;i--)//反向存 
	{
		if(str[i]=='.')
		{
			pos=i;continue;
		}
		else
		{
			A[j++]=str[i]-'0';
		}
	}
	flag=j-1-pos;//flag是数组中，小数点后面一个数的位置，用于一会的四舍五入
	fun();
	if(A[flag]>=5) //如果大于5，进行一次四舍五入 
	{
		t=1;
		for(int i=flag+1;i<j;i++)
		{
			int x=A[i]+t;
			t=x/10;A[i]=x%10;
		}
		if(t==1)
		{
			A[j++]=t;
		}
	}
	for(int i=j-1;i>flag;i--) printf("%d",A[i]);
	return 0;
}

感谢您的阅读，创作不易，转载请注明出处。