第十五届蓝桥杯C/C++B组题解——数字接龙

题目描述

小蓝最近迷上了一款名为《数字接龙》的迷宫游戏，游戏在一个大小为N × N 的格子棋盘上展开，其中每一个格子处都有着一个 0 . . . K − 1 之间的整数。游戏规则如下：

1. 从左上角 (0, 0) 处出发，目标是到达右下角 (N − 1, N − 1) 处的格子，每一步可以选择沿着水平/垂直/对角线方向移动到下一个格子。

2. 对于路径经过的棋盘格子，按照经过的格子顺序，上面的数字组成的序列要满足：0, 1, 2, . . . , K − 1, 0, 1, 2, . . . , K − 1, 0, 1, 2 . . . 。

3. 途中需要对棋盘上的每个格子恰好都经过一次（仅一次）。

4. 路径中不可以出现交叉的线路。例如之前有从 (0, 0) 移动到 (1, 1)，那么再从 (1, 0) 移动到 (0, 1) 线路就会交叉。

为了方便表示，我们对可以行进的所有八个方向进行了数字编号，如下图2 所示；因此行进路径可以用一个包含 0 . . . 7 之间的数字字符串表示，如下图 1是一个迷宫示例，它所对应的答案就是：41255214。

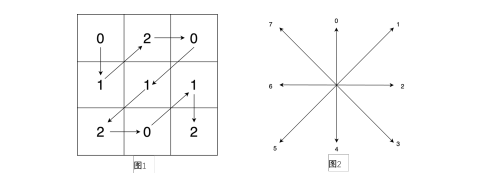
现在请你帮小蓝规划出一条行进路径并将其输出。如果有多条路径，输出字典序最小的那一个；如果不存在任何一条路径，则输出 −1。

输入格式

第一行包含两个整数 N、K。接下来输入 N 行，每行 N 个整数表示棋盘格子上的数字。

输出格式

输出一行表示答案。如果存在答案输出路径，否则输出 −1。

样例输入

3 3
0 2 0
1 1 1
2 0 2

样例输出

41255214

提示

【样例说明】行进路径如图 1 所示。
【评测用例规模与约定】对于 80% 的评测用例：1 ≤ N ≤ 5。对于 100% 的评测用例：1 ≤ N ≤ 10，1 ≤ K ≤ 10。

题目分析

我们看到题目的图片，自然的会想到利用搜索来解决这道题目，再看题目的数据1 ≤ N ≤ 10，1 ≤ K ≤ 10，更加确定了我们用搜索的决心。

但是读完题后，相信大家都会觉得这题条件非常的多，其实这是一件好事，这意味着，我们剪枝的方向也有很多。

那我们先来归纳一下题目的条件

1.要求从(0,0)->(n-1,n-1)，并且要求走过所有的点

很显然，这个就是我们一会dfs的结束条件，递归调用的出口。我们只要在到达了(n-1,n-1)这个点，和走过的点数达到n*n个点的时候，返回即可。

2.要求有多解的情况下，输出子典序最小的路径

这个也很简单，相信写过dfs的同学都知道，我们只需要根据题目这个图片，按顺序建立方向数组，那么第一次搜到的就是字典序最小的。你看，这样又暗含了一个剪枝——只要第一次找到了，后面就不用回溯再找了。

方向数组是这样写

        // 0  1 2 3 4 5 6  7
int dx[]={-1,-1,0,1,1,1,0,-1};
        //0 1 2 3 4  5  6  7
int dy[]={0,1,1,1,0,-1,-1,-1};

3.要求走过数字的顺序必须是0，1，2，……，k-1，0

这个也比较好实现，我们只要比对当前点和下一个坐标点的值即可。此处不过多赘述，详见代码。

4.无解输出-1

这在赛场上就是送分的信息，如果一时间没有很好的思路，那么输出-1，抢分，不失为一种很好的策略。

5.要求走的路径不能交叉

这也是这个题目的难点，什么叫做交叉？是不是如果同时出现了图中红线，与蓝线的走法，那就出现了交叉。

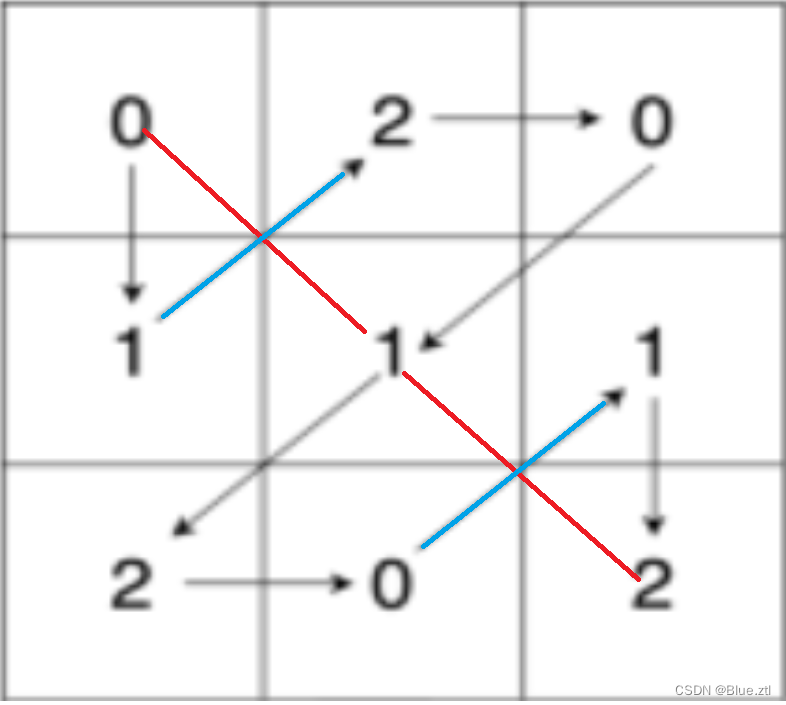
那么在这道题中，哪种走法会出现交叉？请读者细想一下，是不是只有斜着走的时候会出现交叉？

显然是的，斜着走的走法有1，3，5，7。那我们的问题从每次走都判交叉，是不是变成了只用斜着走（1，3，5，7）的时候判交叉即可！

如何判断交叉？多说无益，请看图片。

图中，我画出了（1，3，5，7）走法的原点和下一个点，此外，我还标记了两个点，请读者细想，如果这两个点同时被访问过了，是不是说明，两点中间有一条路径，并且与当前路径形成了交叉。反之则说明，此路径为合法路径。

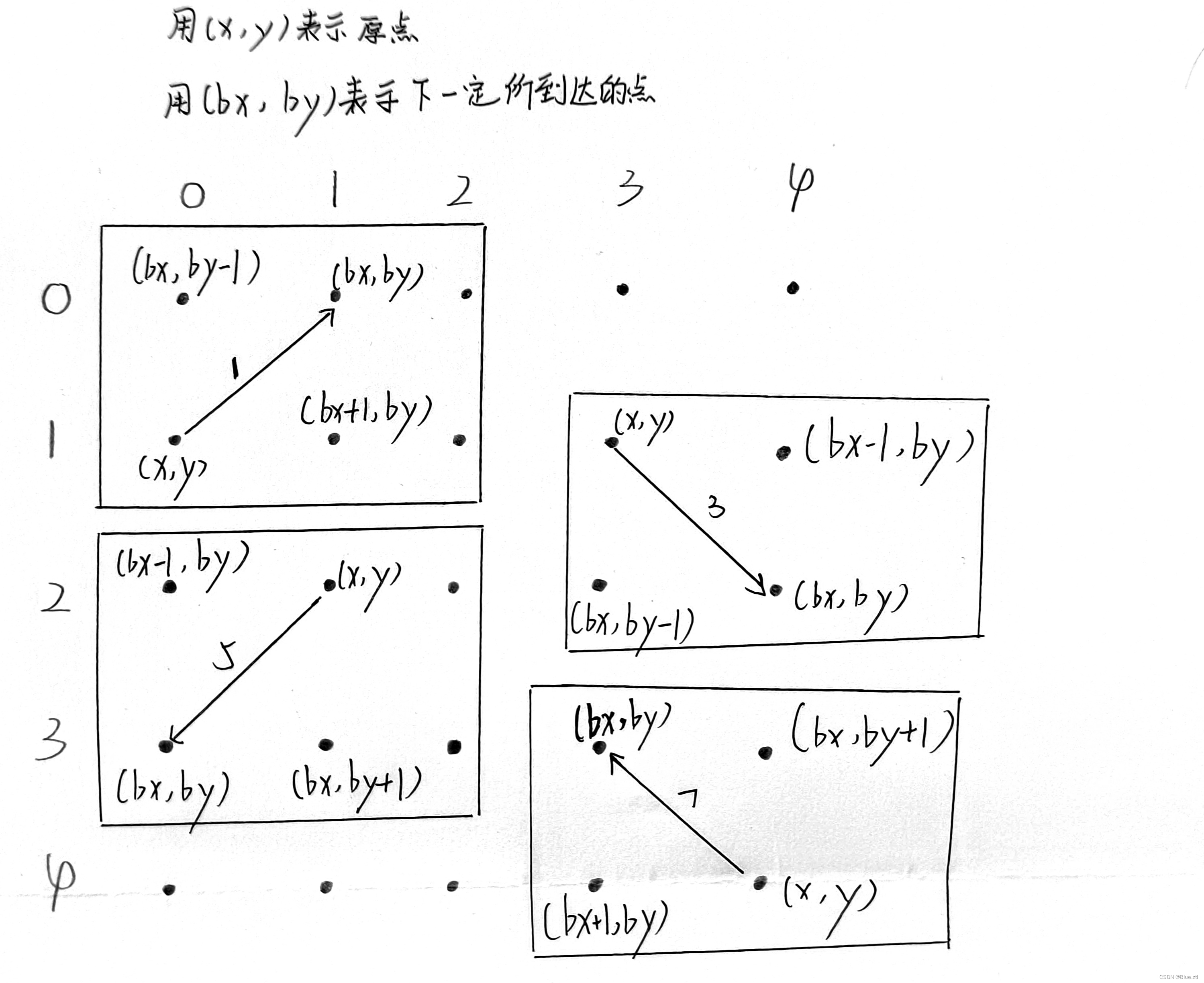
分析毕，下面给出AC代码。

代码中，作者运用的是字符串类型来存储，所走的路径。初始时，是一个空字符串，每次走过一个点就对字符串进行拼接。

s+to_string(i)

 到达终点后如果原先的答案字串ans为空，那么就将s赋值给ans

#include <iostream>
#include <string>
using namespace std;
const int N=20;
string ans;
int g[N][N];//图 
bool vis[N][N];//访问标记 
        // 0  1 2 3 4 5 6  7
int dx[]={-1,-1,0,1,1,1,0,-1};
        //0 1 2 3 4  5  6  7
int dy[]={0,1,1,1,0,-1,-1,-1};
int n,k;//题目输入 
       //起点      //当前值  //当前组成的字串 
void dfs(int x,int y,int cur,string s,int dep)//搜索点的个数 
{
	if(x==n-1&&y==n-1&&dep==n*n)//搜到了(n-1,n-1)，并且搜过了所有的点 
	{
		if(ans.empty()) ans=s;
		return;
	}
	for(int i=0;i<8;i++)//八方向搜索 
	{
		int bx=x+dx[i],by=y+dy[i];
		if(bx<0||bx>n-1||by<0||by>n-1) continue;
		if(vis[bx][by]) continue;
		//判交叉
		if(i==1&&vis[bx][by-1]&&vis[bx+1][by]) continue;
		else if(i==3&&vis[bx-1][by]&&vis[bx][by-1]) continue;
		else if(i==5&&vis[bx-1][by]&&vis[bx][by+1]) continue;
		else if(i==7&&vis[bx+1][by]&&vis[bx][by+1]) continue;
		//保证是0,1,2…k-1,0
		if((cur<k-1&&g[bx][by]==cur+1)||(cur==k-1&&g[bx][by]==0))
		{
			vis[bx][by]=1;
			dfs(bx,by,g[bx][by],s+to_string(i),dep+1);
			if(!ans.empty()) return;//不空表示已经第一次找到了，不用回溯 
			vis[bx][by]=0;
		}
	}
}
int main()
{
	cin>>n>>k;
	for(int i=0;i<n;i++)
	{
		for(int j=0;j<n;j++)cin>>g[i][j];
	}
	string star;//初始空字符串
	vis[0][0]=1;//标记(0,0)已经被访问 
	dfs(0,0,0,star,1);
	if(!ans.empty()) cout<<ans;
	else cout<<"-1";
	return 0; 
}

 感谢您的阅读，创作不易，转载请注明出处。如有错误，烦请大家批评与指正。

一一一一一一一一一一一一一一一一一一一错则改之一一一一一一一一一一一一一一一一一一一一

时间：2025.2.5

感谢部分读者发现，将我上述代码提交至蓝桥官网后，只能通过75%，经笔者调试，笔者发现上述代码确实存在错误。错误在于判断交叉的时候出现了错误。我简单的以为只要其邻近的两个点都被访问过就算出现了交叉。但是并非如此简单，因为很可能出现以下情况。

如图，红色路径根据题意是合法的，但是在我原先的代码中，却将其误判为不合法。

所以我们不能这样简单的去判断是否出现了交叉。

于是我想了个新方法，我新建立了一个path数组来记录每个点所移动的方向，诚然还是只有斜着走的时候才会出现交叉，也就是1357，所以只要在1357时判断，对角线上的两个点是否存在，你来我往的路径，这个过程，相信熟悉本题的读者朋友不难理解，可以参考，我之前画的对角图来理解。

修改后，代码如下。主要修改的地方在判断交叉，并且每次成功的回溯要记录方向

#include <iostream>
#include <string>
using namespace std;
const int N=20;
string ans;
int g[N][N];//图 
bool vis[N][N];//访问标记 
int path[N][N];//记录每个点的移动方向 
        // 0  1 2 3 4 5 6  7
int dx[]={-1,-1,0,1,1,1,0,-1};
        //0 1 2 3 4  5  6  7
int dy[]={0,1,1,1,0,-1,-1,-1};
int n,k;//题目输入 
       //起点      //当前值  //当前组成的字串 
void dfs(int x,int y,int cur,string s,int dep)//搜索点的个数 
{
    if(x==n-1&&y==n-1&&dep==n*n)//搜到了(n-1,n-1)，并且搜过了所有的点 
    {
        if(ans.empty()) ans=s;
        return;
    }
    for(int i=0;i<8;i++)//八方向搜索 
    {
        int bx=x+dx[i],by=y+dy[i];
        if(bx<0||bx>n-1||by<0||by>n-1) continue;
        if(vis[bx][by]) continue;
        //判交叉
        if(i==1&&(path[bx][by-1]==3||path[bx+1][by]==7)) continue;
        else if(i==3&&(path[bx-1][by]==5||path[bx][by-1]==1)) continue;
        else if(i==5&&(path[bx-1][by]==3||path[bx][by+1]==7)) continue;
        else if(i==7&&(path[bx+1][by]==1||path[bx][by+1]==5)) continue;
        //保证是0,1,2…k-1,0
        if((cur<k-1&&g[bx][by]==cur+1)||(cur==k-1&&g[bx][by]==0))
        {
            vis[bx][by]=1;
            path[x][y]=i;//记录当前点所移动的方向 
            dfs(bx,by,g[bx][by],s+to_string(i),dep+1);
            if(!ans.empty()) return;//不空表示已经第一次找到了，不用回溯 
            vis[bx][by]=0;
            path[x][y]=-1;//回溯则重置 
        }
    }
}
int main()
{
    cin>>n>>k;
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<n;j++)
        {
            cin>>g[i][j];
            path[i][j]=-1;//初始化记录 
        }
    }
    string star;//初始空字符串
    vis[0][0]=1;//标记(0,0)已经被访问 
    dfs(0,0,0,star,1);
    if(!ans.empty()) cout<<ans;
    else cout<<"-1";
    return 0; 
}

感谢您的支持与指正。