n6.树（下）

1.堆

优先队列：特殊的队列，取出元素的顺序是按照元素的优先权（关键字）的大小，而不是元素进入队列的先后顺序。
基本操作有两个：插入和删除（最大或最小值）。

实现方式

四种方案中，总有O(n) ，有没有更好的方法？

引入——堆

使用完全二叉树储存数据，并且每个节点的数据都大于他左右子树的值。（优先权为：最大的靠前）
特点：

1. 父节点的值大于子节点的值。保证堆顶元素（根节点）是整个堆中的最大值。
2. 最大堆是一种弱序堆，它只保证父节点的值大于等于子节点的值，而不要求子节点之间的大小关系。
   

和二叉搜索树一样，堆也具有有序性。
例子

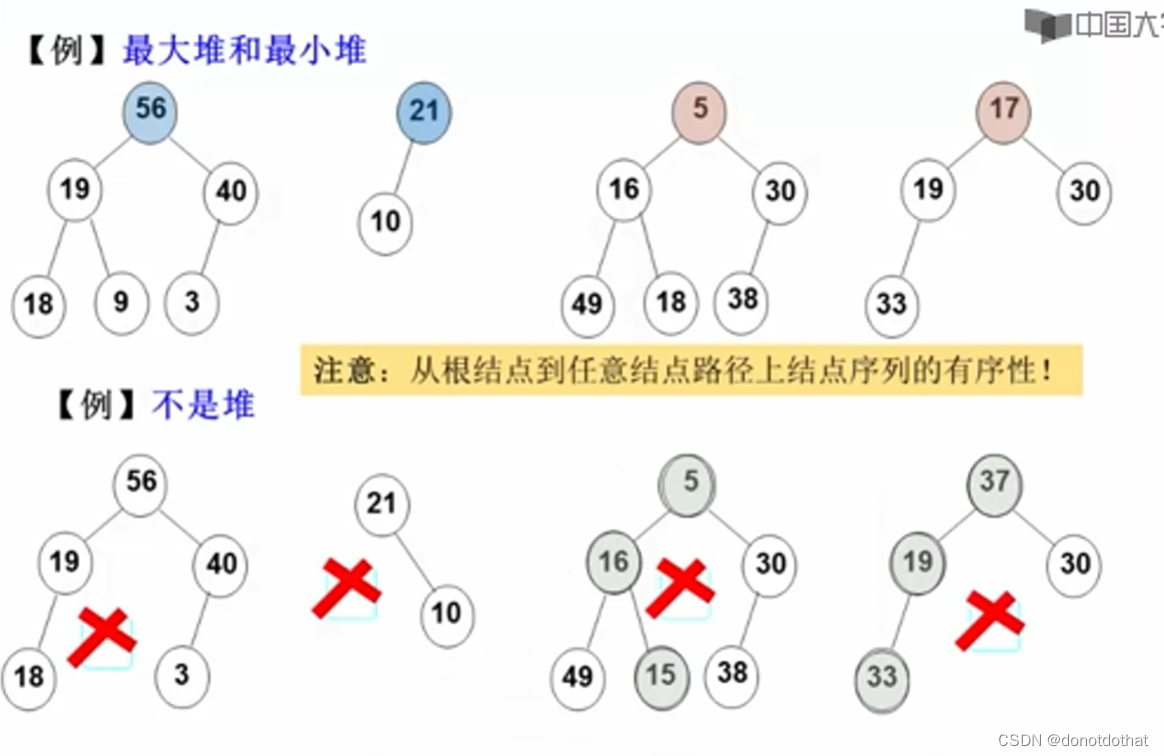
堆的特点是：从根节点向下走一条路径，结点都是有序的。或是从大到小，或是从小到大。
正是这个有序性，使得插入和删除变得方便。

抽象数据类型描述

最主要的操作就是插入和删除

2.最大堆的操作

初始化结构

使用数组来存储完全二叉树（就因为他是完全二叉树）

struct HeapStruct
{	
	ElementType* Elements;//储存堆的数据——一维数组
	int Size;//堆的当前元素的个数，同时也是最后元素的下标（因为是从1开始储存）
	int Capacity;//堆的最大容量
};
typedef struct HeapStruct* MaxHeap;

创建

MaxHeap Creat(int MaxSize)
{
	MaxHeap H = malloc(sizeof(struct HeadStruct));//为结构申请空间
	H->Elements = malloc( sizeof(ElementType)*(MaxSize+1) );//注意从下标为1开始存放数据，数组申请空间，这样索引最大值为MaxSize
	H->Size = 0;
	H->Capacity = MaxSize;
	H->Elements[0] = MaxData;//定义哨兵为大于数组中的所有元素的值，便于操作  
	return H;
}

插入

重点就是不要破坏完全二叉树的有序性。保证插入新节点之后所在子树上满足根节点大于子节点。

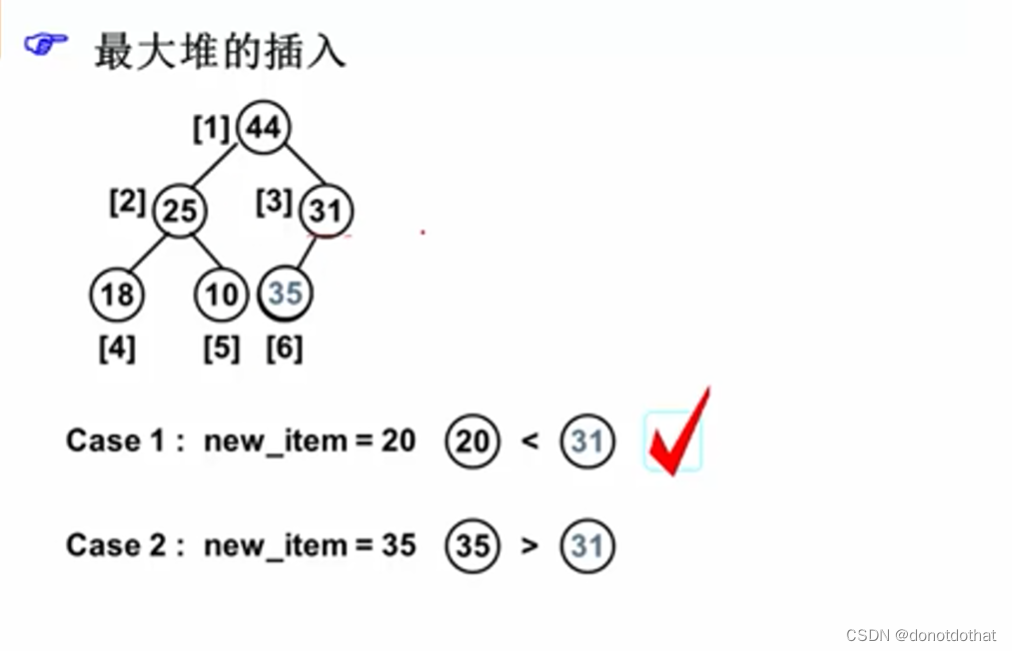
要和父节点进行比较，保证路径的递降有序性。
算法：将新增节点插入到有序序列中
不需要比较左右子节点的大小关系，只需要比较自身和父节点的大小。

void Insert(MaxHeap H , ElementType item)
{//最大堆已经定义了哨兵Elements[0]
	if( IsFull(H) )
	{
		printf("最大堆已经满了");
		return ;
	}
	int i = ++H->Size;//将最后一个元素的下标+1，要插入的下标
	for( ;item > H->Elements[i/2] ;i = i/2)
	{
		H->Elements[i]/*当前节点位置*/ = H->Element[i/2]; //将父节点数据挪到当前位置，item向上比较
	}
	//最后结束的条件：当item的值不再比父节点大，item <= H->Elements[i/2],直接将item安置在当前位置即可
	H->Elements[i] = item;
}

哨兵的作用

当插入的新节点的值大于整个树中所有节点的值的时候，意味着他要取代根节点成为新的根结点。
这时候哨兵节点H->Elements[0] = MaxData就起作用了，默认它一直是最大的节点值，所以他就会大于新插入的节点。就无需条件i > 1

eg，25就一直向上比较，直到成为新的根节点。
时间复杂度是O(logN)，即树的高度

删除

取出根节点（最大值），同时删除
要保证二叉树的完全性、顺序性

1. 将堆中最后一个元素放到堆顶（完成了结构性）
   

2. 找出这个节点较大的孩子节点（要保证顺序性）
   

3. 直到有序性完成
   

时间复杂度为树的高度；
代码实现：

ElementType DeleteMax( MaxHeap H )
{
	int Parent,Child;
	ElementType MaxItem,temp ;
	if( IsEmpty(H) )
	{
		printf("最大堆已经空了");
		return ;
	}
	MaxItem = H->Elements[1];//保存最大值，最后返回
	temp = H->Element[Size--];//想要将最后的节点移到堆顶；另外由于元素减一，Size-1;
	//以上完成了结构性，下面开始完成有序性：
	for(Parent = 1; Parent*2 <= H->Size;Parent = Child )
	{
		Child = Parent * 2 ;
		if( (Child != H->Size )&& (H->Elements[Child] < H->Elements[Child+1]) )
			Child++;
		if( (temp >= H->Elements[Child] ) 
			break;
		else
		H->Elements[Parent] = H->Elements[Child];
	}
	H->Elements[Parent] = temp;
	return MaxItem;
}

对于for循环：
1.Parent = 1;指示着要将temp放到的位置，一开始假设要将temp放到Parent==1的位置，因为先把他放到堆顶；
2.接下来开始确定Parent的值。先判断有没有左右儿子Parent*2 <= H->Size：这是条件，如果索引下标查出了范围，表示没有左右儿子；满足此条件可以退出循环；
3.如果有左儿子，进入循环。每次循环从左右儿子里面挑一个大的与Parent位置的元素比较；
4.Child = Parent * 2 ;Child就表示左儿子的位置，右儿子如果存在，就是Child+1所在的位置；
5.前面的Child != H->Size这个条件保证一定有右儿子：因为Child!=Size就表示没有到边界，Child+1就存在；H->Elements[Child] < H->Elements[Child+1]进行左右儿子的比较，如果右儿子大，那么Child++;Child就表示为右儿子所在位置；否则还是左儿子；进行完这一步if语句就完成了选出左右儿子中大的一个孩子这一步；
6.接下来要判断temp是不是比找出的左右儿子中的最大者还要大，如果temp更大，跳出循环，说明temp已经到了正确的位置；如果temp小，那么temp要下去，H->Elements[Parent] = H->Elements[Child];把找出的较大者放在当前Parent这个位置，进入循环的下一轮；
7.要进入下一轮，先将temp移动到Child的位置Parent = Child ，继续循环；
8.最后退出循环，说明找到了temp要存放的位置，完成赋值操作；

最大堆的建立

将已经存在的N个元素按最大堆的要求存放在一个一维数组中。

较好的方法是先满足结构特性，再满足顺序特性。
和删除的思路很像，删除的核心就是在堆顶新来一个元素（并且满足左右子树是堆），如何实现顺序性。
从倒数第一个有儿子的节点开始，（这个节点的左右儿子已经满足了堆），然后将此节点和左右儿子调成堆；然后向前走，将三角形节点都调成堆（三节点组成最小堆）；

直到将最下边小三角层都调成堆：

然后向上一层调成堆：

这样对于根节点的左右子树来说，左右子树都分别是堆。然后再将根节点找个合适的位置去存放，类似删除的存放过程；
整个过程是先将根节点的左右子树变成堆，然后找位置。变成堆的过程，将大的问题变成小的问题，逐层操作；
时间复杂度为：树中各节点的高度和

3.哈夫曼树与哈夫曼编码

引子

根据数据分布的频率、比例，可以设置不同的搜索树

修改判定树的过程，可以提高效率，所以可以根据节点不同的查找频率构造更有效的搜索树。

哈夫曼树

这里的权值wk就是指的频率，哈夫曼树就是使得每个节点的频率 * 路径长度 之和最小。

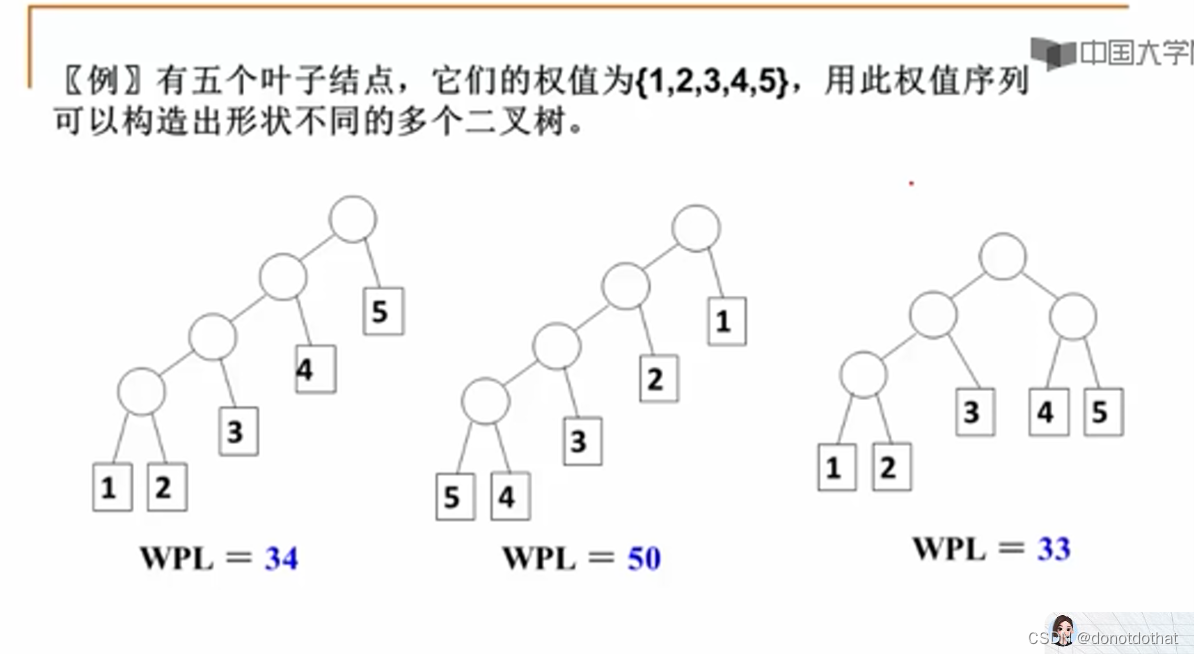
哈夫曼树的构造

方法：
例如对于1 2 3 4 5

每次把权值最小的两个二叉树合并，并将权值相加，重复操作。例如，这里五个节点的权值分别为1,2,3,4,5。
1）一开始选1,2 —>3
2) 在新的权值列表中3,3,4,5继续选两个，即选3,3–>6;
3) 再在6，4，5中选4,5得9；
4）最后将两个二叉树合并；

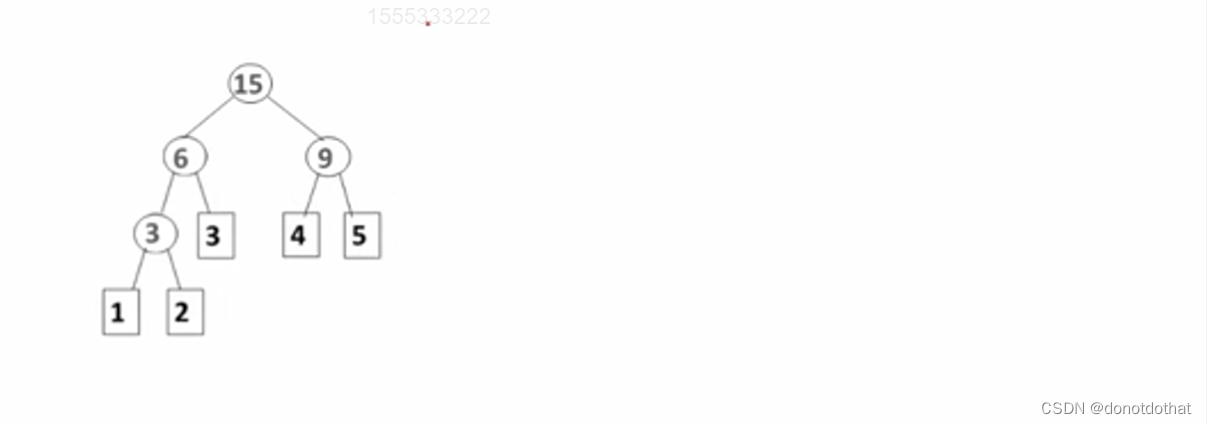
代码实现：

typedef struct TreeNode* HuffmanTree;
struct TreeNode
{
	int Weight;//权值
	HuffmanTree Left;Right;左右子树
};
Huffman Huffman( MinHeap H )
{//假设H->Size个权值已经存在H->Elements->Weight
	int i;
	HuffmanTree T;
	BuildMinHeap(H);//基于权值，调整为最小堆
	for(i = 1;i<H->Size;i++)//循环H->Size-1次，就完成
	{
		T = malloc( sizeof( struct TreeNode ) );//建立新节点
		T->Left = DeleteMin(H);
		T->Right = DeleteMin(H);
		T->Weight = T->Left->Weight + T->Right->Weight;
		Insert(H,T);
	}
	T = DeleteMin(H);
}

进行循环操作：如果有Size个数据，那么就要进行Size-1次合并（3个进行2次；4个进行3次…）。每次合并都是运用堆的相关操作，从堆中删除2个最小的节点，并且返回给要创建的二叉树。拿出来两个最小的节点，将他们的权值相加，得到父节点的权值，将这个父节点再插入到堆中，继续操作合并。最后循环退出，最小（堆顶）元素就是哈夫曼树的树根节点。

哈夫曼树的特点

1.没有度为1的结点
因为哈夫曼树是两两组成，权值和相加；
2.n个叶节点的哈夫曼树共有2n-1个节点
因为哈夫曼树还是属于二叉树，根据二叉树的性质，叶节点n0，度为1的节点n1，度为2的节点n2，有n0 = n2+1.又因为哈夫曼树没有度为1的节点，那么，总结点数就是n+n-1 = 2n-1
3.哈夫曼树的任意非叶节点的左右子树交换之后还是哈夫曼树
因为在构建哈夫曼树的过程中，并没有要求左右子树的大小相对关系。
4.不同构的哈夫曼树

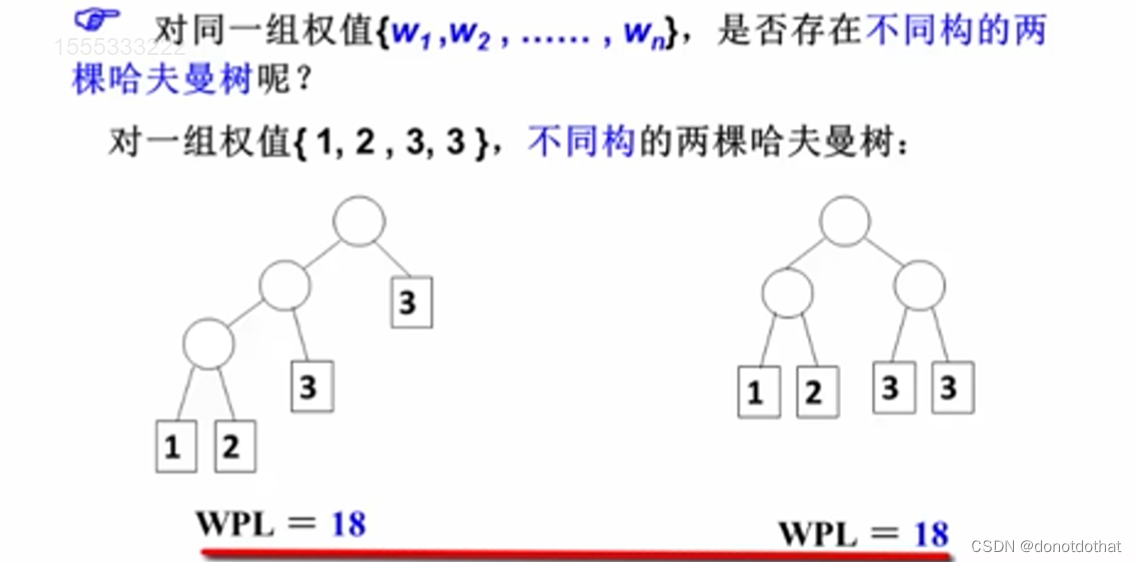
这两个哈夫曼树是不同的，但是平均执行效率是相同的。

哈弗曼编码

引子

注意编码过程中要避免二义性：

如何避免二义性？

前缀码：任何字符的编码都不是另一字符编码的前缀，就可以无二义地编码

二叉树用于编码

1等长编码

要保证所有的编码不具有二义性，就要使所有的字符都是处于二叉树的叶节点上。

其实计算方法就类似哈夫曼树的计算方法。

2不等长编码—哈夫曼编码

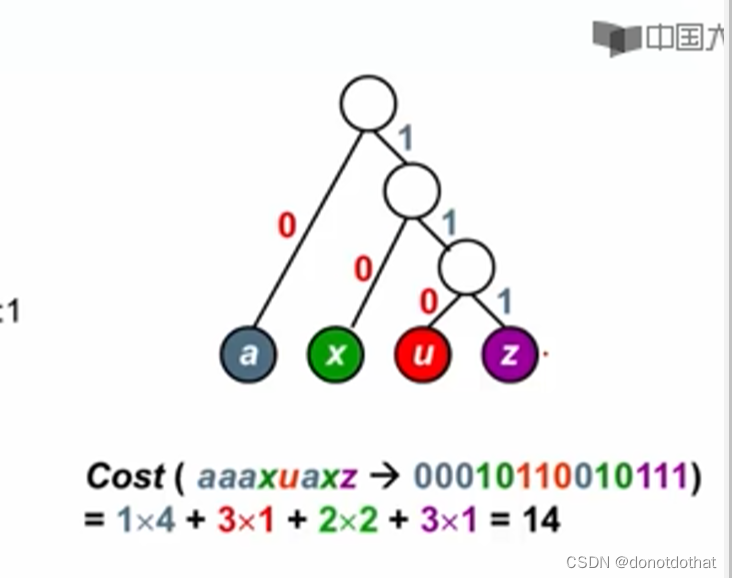
只要满足编码的符号在叶节点上面，就能够避免二义性。 使用哈夫曼树，就可以构造出代价（cost）最小的二叉树。
哈弗曼编码：

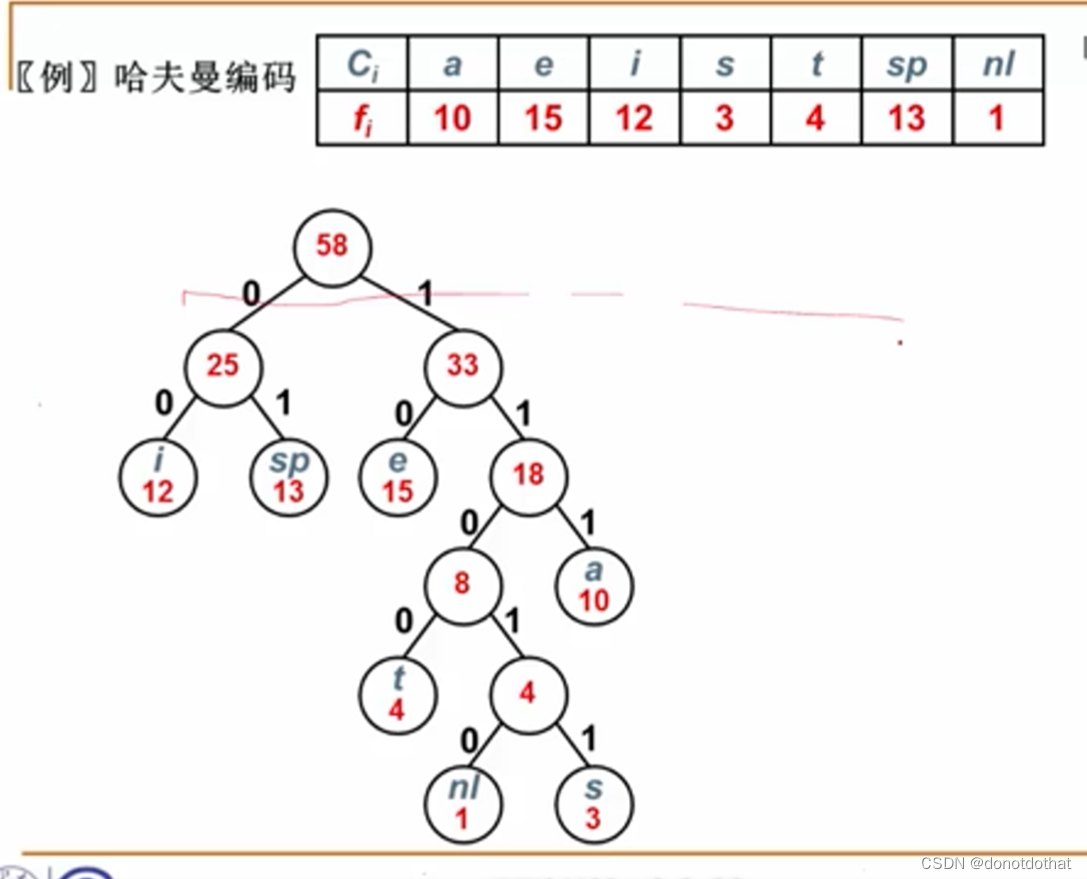
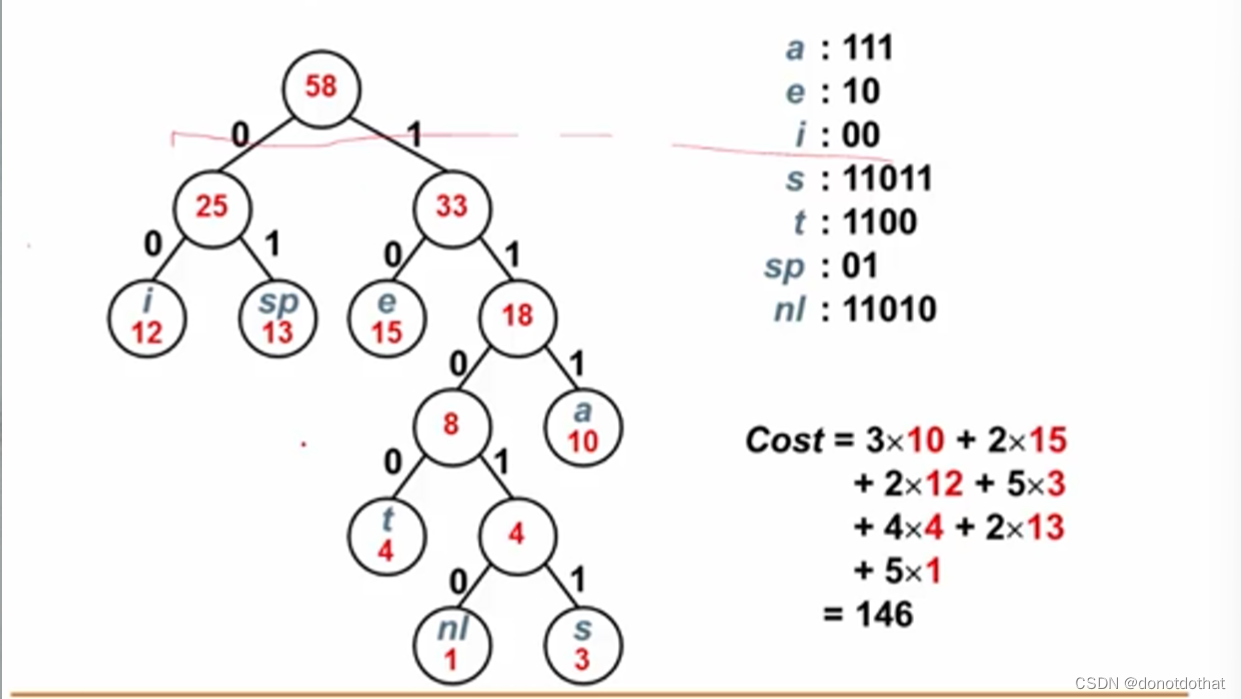
基于频率构造哈夫曼树，然后左0右1，可以得到哈弗曼编码。显然，得到编码都位于哈夫曼树上的叶节点。

4.集合及运算

集合的表示及查找

注意这种连接具有传递性，a和b相连，b和c相连，那么a就和c相连。

并、查集 集合储存的实现

可以使用树来储存集合，一棵树就表示一个集合，使用树的根节点来代表这个集合。

• 查：查找一个元素在哪个集合中，就是查找这个节点的根节点是谁。更重要的是已知一个节点去找到他的父节点是谁。
• 并：将两个集合并在一起就是将两棵树并在一起；
  

这种树的结构是由儿子指向父亲， 这就是双亲表示法，孩子指向父亲。

• 除了使用链表来实现储存，同样可以使用数组来实现：
  因为不像以前的父亲指向孩子那样，一个节点要指向多个节点，现在一个节点只需要指向他的父亲，那么一个下标就可以表示父节点。
  在数组中，每个数组元素是一个结构，储存着结点数据以及父节点的下标
  
  根节点没有父节点，Parent用-1来表示。可以看到，这一个数组就完成了三个树即三个集合的储存。
• 代码实现

查找：

int Find( SetType S[],ElementType x )
{//在整个数组中寻找x是哪个集合的，就是要查出x所在树的根节点  MaxSize表示数组的长度
	int i ;
	for(i = 0;i<MaxSize && S[i].Data!=x ;i++);//寻找x在哪，找到之后再找父节点
	if(i>=MaxSize) return -1;//找不到
	for( ; S[i].Parent>=0;i = S[i].Parent);
	//这个for循环最后一次循环应该是S[i].Parent == 0也就是父节点就是根结点，那么就需要再找一次，就找到了根结点
	return i ;//返回的i就是x所在集合的根节点所在数组S的下标
}

并集：
首先要找到所需要并集操作的元素x1、x2所在树的根节点；如果他们同根，就表示他们本就在同一个集合里面，无需进一步操作；如果他们不同根，就需要将两棵树连接起来，可以将其中一个根的父节点指针设置为另一个根节点的数组下标。

void Union( SetType S[],ElementType x1,ElementType x2 )
{
	int Root1,Root2;
	Root1 = Find(S,x1);
	Root2 = Find(S,x2);
	if( Root1 != Root2 )
		S[Root1].Parent = Root2;
}

例如：

两个集合的并集操作，会使得树的高度变大，为了改善合并之后的查找性能，可以让小的集合合并到相对大的集合中去。这就可能会使得合并之后的树的高度不会增加，还是树大的那个高度。
那如何判断集合中有多少个元素呢？
可以使用这样的一种方法，将根节点的Parent部分改成-总结点个数：

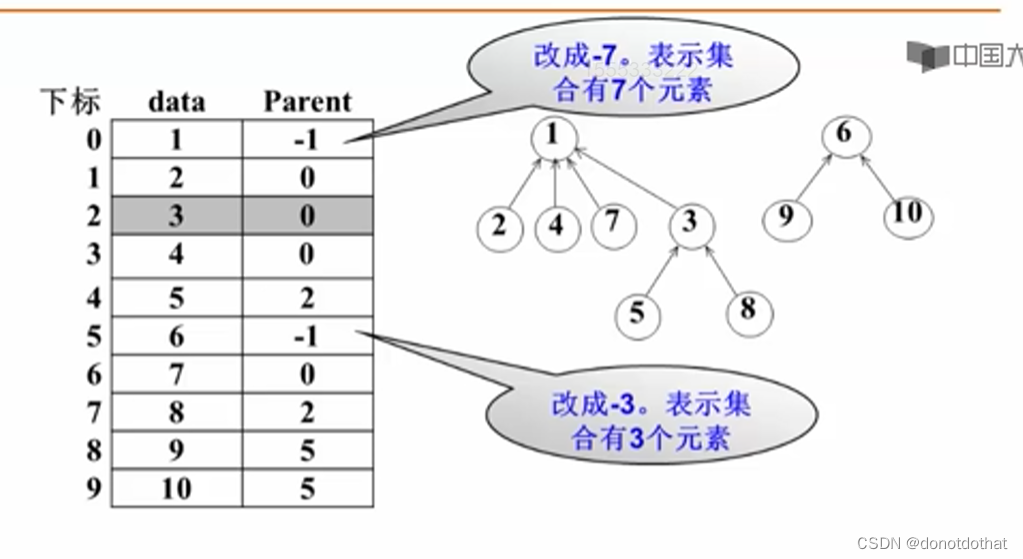
负数代表他是根节点，绝对值表示树有多少个节点。这样就不需要扩大空间来储存节点个数的信息了。
这样就需要在合并之前，比较节点个数的多少来决定谁挂在谁的下面了。