dfs超详解（基本用法+蓝桥杯真题）

dfs
dfs即深度优先搜索（Depth first search），搜索算法中的一种，用递归进行搜索，是尽可能深的搜索每一个节点，可以理解为不撞南墙不回头。
用于解决一些树的遍历和图的遍历，由于是通过递归实现，时间复杂度较高，一般题中所给数据较小。
dfs在蓝桥杯中出现率很高，正如图中所示，无论是省赛国赛都出现了很多于dfs相关的题目，而且出现的难度会相对高一些。

如何理解dfs

对于刚接触dfs算法的人，个人感觉应该跟b站的up主画一下递归搜索树，画递归搜索树有助于理解dfs中的深度优先。例如下面的排列问题

排列问题

排序问题是dfs中比较简单的应用，主要帮助理解dfs

输入一个数字，输出其全排列（字典序） 

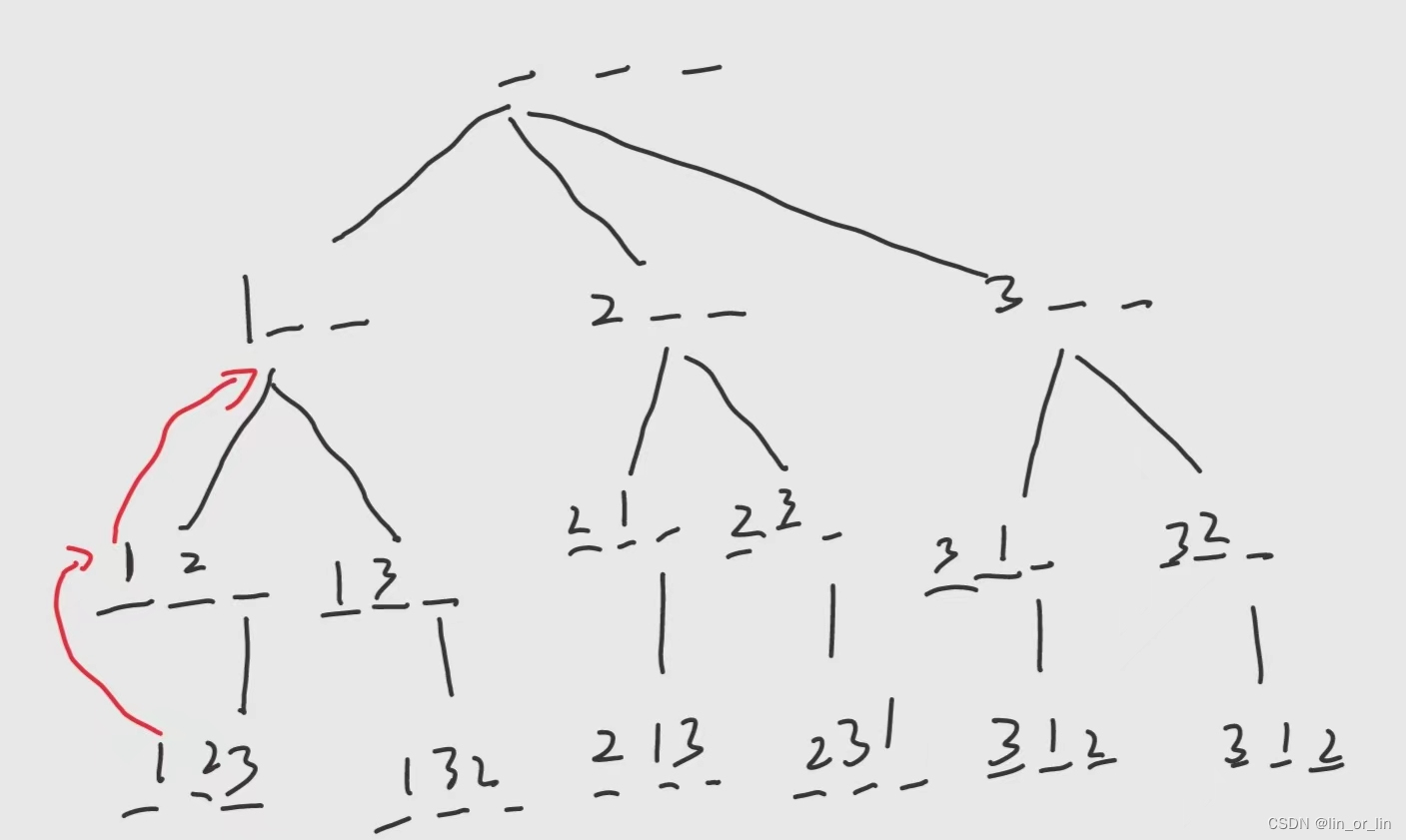
这个是对应递归搜索树（图丑轻喷），就是最开始选第一位，有1，2，3，三种选择，如果先选择1，之后选第二位有2，3，两种选择，选择2，最后第三位只能选择3，然后输出第一种排列，之后回溯回到第二位的选择，第二位选择3，第三位就选择2，输出，之后回溯到第一位选择，第一位选择2…以此类推。
就是不撞南墙不回头，撞到南墙输出一个结果，之后回到上一个位置继续撞南墙。

#include<bits/stdc++.h>
using namespace std;
int a[20];//储存数字
int book[20];//标记是否选过数，1是已选，0是未选
int n;//输入数字
void dfs(int step)
{
   
    if(step == n + 1)
    {
   
        for(int i = 1; i <= n;i++)
        {
   
            cout<<a[i];
        }
        cout<<endl;
        return ;
    }
    for(int i = 1; i <= n;i++)
    {
   
        if(book[i] == 0)
        {
   
        a[step] = i;
        book[i] = 1;
        dfs(step + 1);
        book[i] = 0;//回溯
        }

    }
    return ;
}
int main()
{
   
    cin>>n;
    dfs(1);
    return 0;
}

由于递归十分的抽象，如果像我一样抽象思维不是很好的话，可以试着把程序在纸上跑一遍，一步一步的执行，这样会加深对dfs的理解，也可以跟着b站上边的老师把程序走一遍，下图就是我自己一步步写出的程序执行的过程（差不多写到132的时候就基本理解了，过程其实有点绕，尽量耐心一些）

对应的运行结果

迷宫问题

给出一个迷宫（n行m列），标记1是障碍，标记0可以通过

0100
0001
1100
0011
1010

从入口到出口
求最短路径

输入：迷宫大小出入口以及迷宫元素
输出：最短路径否则输出NO

想解决迷宫问题要先理解方向数组
方向数组
其中（x，y）并非是数学坐标系的横纵坐标，而是第x行第y列，针对于二维数组

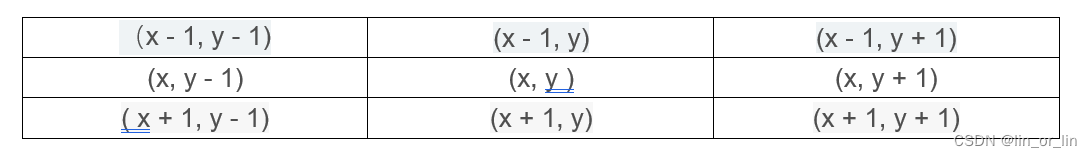
方向数组跟正常理解的左加右减上加下减正好是反过来的，是按照数组的下标来操作的
方向数组可以写成两个一维数组也可以写成一个二维数组，按照个人的喜好选择就行

int next1