PTA 7-1 地下迷宫探索(C语言）

夜烨123

于 2024-11-16 11:37:52 发布

阅读量1.4k

点赞数 19

分类专栏：数据结构文章标签： c语言深度优先算法图论数据结构

本文链接：https://blog.csdn.net/2302_80273625/article/details/143666828

版权

数据结构专栏收录该内容

16 篇文章

订阅专栏

题目如下：

地道战是在抗日战争时期，在华北平原上抗日军民利用地道打击日本侵略者的作战方式。地道网是房连房、街连街、村连村的地下工事，如下图所示。

我们在回顾前辈们艰苦卓绝的战争生活的同时，真心钦佩他们的聪明才智。在现在和平发展的年代，对多数人来说，探索地下通道或许只是一种娱乐或者益智的游戏。本实验案例以探索地下通道迷宫作为内容。

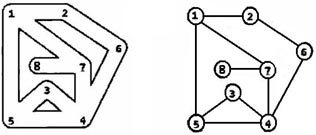
假设有一个地下通道迷宫，它的通道都是直的，而通道所有交叉点（包括通道的端点）上都有一盏灯和一个开关。请问你如何从某个起点开始在迷宫中点亮所有的灯并回到起点？

输入格式:

输入第一行给出三个正整数，分别表示地下迷宫的节点数N（1<N≤1000，表示通道所有交叉点和端点）、边数M（≤3000，表示通道数）和探索起始节点编号S（节点从1到N编号）。随后的M行对应M条边（通道），每行给出一对正整数，分别是该条边直接连通的两个节点的编号。

输出格式:

若可以点亮所有节点的灯，则输出从S开始并以S结束的包含所有节点的序列，序列中相邻的节点一定有边（通道）；否则虽然不能点亮所有节点的灯，但还是输出点亮部分灯的节点序列，最后输出0，此时表示迷宫不是连通图。

由于深度优先遍历的节点序列是不唯一的，为了使得输出具有唯一的结果，我们约定以节点小编号优先的次序访问（点灯）。在点亮所有可以点亮的灯后，以原路返回的方式回到起点。

输入样例1:

输出样例1:

1 2 3 4 5 6 5 4 3 2 1

输入样例2:

输出样例2:

6 4 5 4 6 0

错误思路：

下面是我自己的错误思路，怕被绕进去的可以略掉，嘻嘻！

首先，我看到这道题的第一反应就是离散数学中讲的欧拉图（一笔画问题），我还在想当时有讲相关的代码实现吗？结果看到后面“深度优先遍历的节点序列是不唯一的”我才知道考查深度优先遍历的。

可以看出所给的输入是类似边集数组的形式。

然后，我就想转成邻接表（选邻接表，是我觉得遍历的时间复杂度更小，别问，问就是学数据结构学魔怔了），我已经替大家尝试过了，显然转成邻接矩阵是更简单的。

接下来我就打算进行深度遍历算法，再用一个数组记录遍历的路径，最后正序输出，再倒叙输出。没想到这也是错的（我也是看了CSDN上大佬发的文章才明白过来）。我认为主要原因是我一开始以为这道题考查的是欧拉图，也就是一个结点只能经过一次，后来才反应过来，这是深度优先遍历，一条路走到头是要返回的，也就是每个节点不只是经过了一次，只是算法只输出了第一次访问的情况，而这道题是经过一次输出一次，这也是这道题的核心所在。

改进思路：

选邻接表太麻烦，一是需要手动创建结构，另外题目要求“约定以节点小编号优先的次序访问（点灯）”，这对于构建邻接表也加大了难度。反观邻接矩阵，直接定义一个二维矩阵，令存在这条边的位置为一即可。
用数组记录遍历的路径也不行，因为深度遍历算法中间会可能回到原来访问过的点，类似于一条路走到头了，又返回分叉点走另一条路，而这路上你经过的每一个点都要输出。这并不是一个数组可以完成的，所以不可取。
在深度遍历算法中相当于只是记下了你第一次经过每条路的次序，而这道题要求把所有你走过的路都记下来输出，不在乎是否重复（毕竟是点灯嘛，不是一笔画，只要全部点亮就行）。也就是这道题要求是输出你电灯的路线，只是深度优先遍历恰好可以实现这一算法。
核心是要在又回到这一点时在进行一次输出，因为深度遍历过程中会回到你已经访问过的这一点看看其邻接点是否还有没访问过的，所以在本题中就不只是再看看，还要输出一次。
还有迷宫不是连通图的情况，我是设了一个全局变量count，每第一次输出这个结点（深度遍历原来输出的位置），count就加一。如果count小于总结点数n，表示是非连通图，就会在最后输出一个0。同时，count还起到控制空格输出的作用，我选择的是要是输出的是第一个元素，即count=0时，前面就不带空格，其余的输出是前面都带空格。
```
if (count != n) printf(" 0");
```
```
if (count == 0) {
		printf("%d", s);
		count++;
	} else {
		printf(" %d", s);
		count++;
	}
```

遍历函数

void DFSL(int s) {
	if (count == 0) {    //第一个不带空格
		printf("%d", s);
		count++;         
	} else {
		printf(" %d", s);
		count++;
	}
	visited[s] = 1;
	for (int i = 1; i <= n; i++) {
		if (M[s][i] && !visited[i]) {
			visited[i] = 1;
			DFSL(i);
			printf(" %d", s);  //算法增加部分，核心所在
		}
	}
}

完整代码

#include <stdio.h>
#include <stdlib.h>
int count = 0;
int M[1001][1001];
int visited[1001] = {0};
int n, m, s;

//深度优先遍历
void DFSL(int s) {
	if (count == 0) {
		printf("%d", s);
		count++;
	} else {
		printf(" %d", s);
		count++;
	}
	visited[s] = 1;
	for (int i = 1; i <= n; i++) {
		if (M[s][i] && !visited[i]) {
			visited[i] = 1;
			DFSL(i);
			printf(" %d", s);   //核心
		}
	}
}

int main() {

	//输入节点、边数、起始序号
	scanf("%d %d %d", &n, &m, &s);
	//输入边，创建邻接表
	for (int i = 0; i <= n; i++) {
		for (int j = 0; j <= n; j++)
			M[i][j] = 0;
	}
	int i, j;
	for (int k = 0; k < m; k++) {
		scanf("%d %d", &i, &j);
		M[i][j] = 1;
		M[j][i] = 1;
	}
	DFSL(s);
	if (count != n) printf(" 0");
	return 0;
}