训练部分题解

匪石的小迷妹.

已于 2024-05-06 13:54:38 修改

阅读量1k

点赞数 26

分类专栏：补题集文章标签：算法

于 2024-05-04 20:28:26 首次发布

本文链接：https://blog.csdn.net/2302_80707071/article/details/138447624

版权

补题集专栏收录该内容

24 篇文章

订阅专栏

2024.4.3

G 小P玩钢4

题目描述：

小 P在合肥玩了一天，晚上回到酒店后决定开一把钢铁雄心4。钢铁雄心是一款二战模拟器，玩家可以操纵部队进攻敌国。玩了没多久，小 P很快便包围了敌军的部队。
具体来说，当前这一片战场可以看成是一块 n×m的网格，每个格子上有一个数字，第 i 行第 j列的数字为 ai,j。如果 ai,j>0，则代表这块格子上有数量为 ai,j 的敌军部队，如果 ai,j=0，则代表这块格子上是我军部队。在这片战场之外也全是我军部队。
显然，这些敌军部队深陷我军的包围之中，我们需要快速消灭包围圈中的敌人。我们每次可以选择一块与我军部队相邻的有敌军的格子（假设是第 i行第 j列），然后一共需要消耗 ai,j加上这个格子四周的敌军部队数量之和个单位的装备消灭掉这个格子上的敌人，随后我军部队进入这个格子，ai,j为 0.
由于战场宽度的限制，导致每个格子最多只有一个敌军部队，即 ai,j∈{0,1}。现在小 P想要知道，最少消耗多少装备能够消灭掉所有敌军部队？

Input

第一行输入两个整数 n,m(1≤n,m≤1000
)，表示战场的行数和列数。接下来 n 行，每行输入 m个整数第 i 行第 j 个数为 ai,j(ai,j∈{0,1})。

Output

输出一行，即最少消耗的装备数量。

Examples

Input
5 5
0 0 0 0 0
0 0 0 1 0
0 1 1 1 0
0 0 1 0 0
0 0 0 0 0
Output
9
Note
在样例中，我们可以先攻击 a3,3的部队，需要消耗 1+3=4
个单位的装备。接下来攻击 a3,4 的部队，需要消耗 1+1=2
个单位的装备。接下来三个剩下的敌军部队任选一个顺序攻击即可。因此总的花费为 9。可以证明不存在更优的方案。

解题思路：

依次遍历数组，攻击敌军，将数组中攻击过的做标记，并且计算消耗的装备。

解题代码：

#include<bits/stdc++.h>
using namespace std;
int a[1010][1010];
int dx[5]={0,1,-1,0,0};
int dy[5]={0,0,0,1,-1};
int jc(int x,int y);
int main()
{
	int m,n,f=0,g,h;
	cin>>m>>n;
	for(int i=1;i<=m;i++)
	{
		for(int j=1;j<=n;j++)
		{
			cin>>a[i][j];
		}
	}
	for(int i=1;i<=m;i++)
	{
		for(int j=1;j<=n;j++)
		{
			if(a[i][j]!=0)
			{
				f=f+jc(i,j);
				a[i][j]=0;
			}
			
		}
	}
		cout<<f<<endl;
	return 0;
}
int jc(int x,int y)
{
	int e=1;
	for(int i=1;i<=4;i++)
	{
		e+=a[x+dx[i]][y+dy[i]];
	}
	return e;
}

J pass

题意描述：

smzzl 驾驶着小车正在环海公路漫游，突然遇到了一个很窄的地方，还好他技术高超，他打算使用 b 站刚看到的单边桥方法通过这段路（你别管怎么上的墙）。由于 smzzl 喜欢漂移，又要防止漂到海里去，他想要驾驶底盘低的车，请你告诉他，在不挂蹭到车底盘的前提下，他最低能驾驶底盘多低的车通过这段路。
由于车是 smzzl 自己改装的，因此 smzzl 将几乎所有的重量都分配在了车的接地处以防翻车。
在本题中，道路被抽象成如下图所示：左侧蓝色粗线的是海洋，中间黑色的是路面，右侧蓝色细线是墙壁（竖的是墙壁侧面，横着的是墙壁顶面）；红色的是车轮，绿色的是底盘，紫色的是车身。车辆允许两个轮胎都在路面上，或者一个轮胎在路面上另一个在墙壁的顶面上。车辆需要满足除了轮胎最下面的接地处，其他地方均不能和墙壁有交，恰好碰到也认为是有交（显然车不能穿模，这可是真实车辆！）。
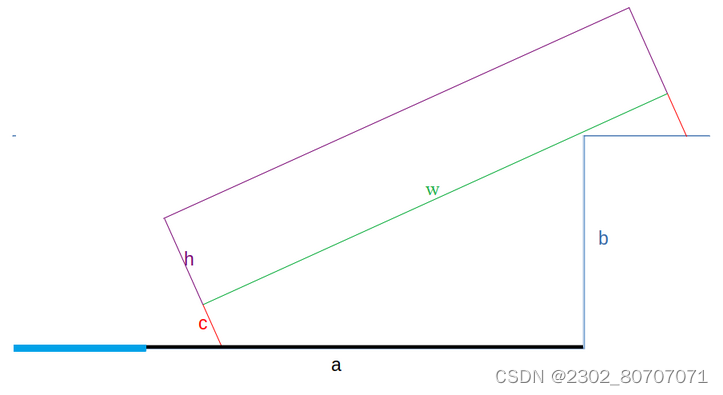
在这里插入图片描述

在本题中，车轮的大小也就代表的底盘高度，也就是图中的参数 c。
给定车和道路的参数，请你告诉 smzzl 最低允许驾驶的车辆底盘高度。路面和车辆参数具体见题目

Input

本题每一个测试点包含多组测试数据。
第一行一个整数 T(1≤T≤1000)，表示数据组数。
对于每一组数据，一行，4 个整数 a,b,h,w(1≤a,b,h,w≤106)，分别表示路面宽度，墙壁高度，车辆高度（不算底盘）和车宽。

Output

T 行，每行一个数表示该组数据的答案。如果无论如何无法通过则输出 −1。
如果你的答案和标准答案的相对误差或绝对误差不超过 10−6，则会被认为是正确的。
形式化的表示：假设你的答案是 a，标准答案是 b，则你的答案会被认为是正确的当且仅当 |a−b|max(1,b)≤10−6

Input

8
4 1 2 8
7 5 3 3
7 5 3 7
7 5 3 12
1 6 3 5
1 6 3 6
1 6 3 7
5 8 5 5

Output

0.4921567416
0.0000000000
0.0000000000
1.6286300478
-1
-1
2.2333296647
-1

解题思路：

如果车宽小于路面宽度，车辆底盘高度为0，即可直接通过，如果不小于则要比较墙壁高度与车宽，为了可以让车借助墙壁，如果不可以输出-1，如果可以用几何关系求出车辆底盘高度。

解题代码：

#include<bits/stdc++.h>
using namespace std;
int t;
double a,b,h,w;
int main()
{
	cin>>t;
	while(t--)
	{
		
		cin>>a>>b>>h>>w;
		if(a>w)
		printf("0.0000000000\n");
		else if(b>=w)
		printf("-1\n");
		else
		{
			double l=sqrt(w*w-b*b)-a;
			if(l<=0)
			printf("0.0000000000\n");
			else
			{
				double r=l*b/w;
			printf("%.10lf\n",r);
			}
		}
	}
	return 0; 
 }

K str进制

题目描述：

str，一个充满着神秘气息的字符串。

它既可以是某位 jiker 的姓名缩写，也可以表示字符串这个单词的缩写，由于其多变的特性，我们可以定义str进制字符串，下面的符合下面进位规则的进制称为该字符串下的 str 进制：
给出一个str进制字符串，每位上的数字x表示该位上是逢x进1。
给定某个字符串s，再给出一个十进制下的整数d，求d
在str进制下的表示值。

Input

第一行输入两个整数m,n (1≤m≤1000,1≤n≤10
)，代表 str 进制字符串的长度和d的位数。第二行输入一个字符串s(2≤si≤9)，表示 str 字符串。
第三行输入一个整数，表示d (0≤d≤1010)。数据保证d能够在str进制下被表示出来。

Output

输出一行一个 m 位的整数，为整数d在 str 进制下的表示。(包括前导零)
Input
4 1
2664
8
Output
0020

解题思路：

根据题上所给的进制方案，将十进制数转化为str进制（倒着进行），最后正序输出所得结果。

解题代码：

#include<bits/stdc++.h>
using namespace std;
int p[1010]={0};
int main()
{
	long long m,n,a,b,c;
	cin>>m>>n;
	string s;
	cin>>s;
	long long d;
	cin>>d;
	b=d;
	for(int i=m-1;i>=0;i--)
	{
		a=b;
		b=a/(s[i]-'0');
		
		c=a%(s[i]-'0');
		
		p[i]=c;
		if(b==0)
		break;
	}
	for(int i=0;i<m;i++)
	{
		cout<<p[i];
	}
	cout<<endl;
	return 0;
}

M 小H的糖果

题目描述：

小H很喜欢吃糖。
有一天，小L给小H准备了一大串糖果，它们从前往后排成一行，每个糖果上都写有一个小写字母。由于单纯的吃糖显得太单调，于是小L制定了一个规则，小H只能选择一个糖果，然后依次吃掉它和它后面的所有糖果。吃掉的这串糖果的组成的字符串字典序越大，小H的满意度就越高。然而小H可不会这么轻易地就同意小L的规则，于是据理力争来了一个条件：可以任意选择恰好一个位置，将上面的糖果替换为写有任意一个小写字母的糖果（允许替换前后的糖果上的字母相同）。
现在，聪明的你告诉小H，该如何替换糖果以及选择起始位置的糖果，得以让小H的满意度最高呢？
对于两个字符串 s1 和 s2，它们的长度分别为 n1和 n2。定义 s1 的字典序比 s2 的小，当且仅当其满足以下两个条件之一：
如果存在一个位置 i，使得对于所有 j<i，s1,j=s2,j，而 s1,i<s2,i。即在第一个不相等的位置上，s1 的字母在字母表中的顺序靠前。如果 s1 是 s2 的前缀，且 n1<n2。

Input

第一行输入一个 n (1≤n≤5000) ，代表糖果的个数。第二行输入一个字符串 s (|s|=n) ，代表糖果上字母的序列。题目保证 s 只包含小写字母。

Output

输出共一行一个字符串，表示让小H满意度最大的糖果串。

Input

10
zzazzzabcd

Output

zzzzzzabcd

Input

8
azzzabcd

Output

zzzzbcd

解题思路：

依次列举，从后面开始不为z的替换为z，比较输出最大的字符串

解题代码：

#include<iostream>
#include<string>
using namespace std;
int main()
{
	int n;
	string s,a;
	cin>>n>>s;
	for(int i=0;i<n;i++)
	{
		string d;
		int f=0;
		for(int j=i;j<n;j++)
		{
			d+=s[j];
			if(d[d.size()-1]!='z'&&f==0)
			{
				d[d.size()-1]='z';
				f=1;
			}
		}
		if(i!=0) 
		{
			if(d>a)
			a=d;
		}
		else
		a=d;
		
	}
	cout<<a;

}

2024.4.4

B Memory

题目描述：

在这里插入图片描述

解题思路：

这道题直接来做，会时间超限，因此根据数据找寻规律，发现b[i]=b[i-1]/2+a[i],然后对小数部分单独处理。

解题代码：

#include<bits/stdc++.h>
using namespace std;
int a[100010];
int main()
{
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
	}
	int b=0;
	double flag=0;
	for(int i=1;i<=n;i++)
	{
		b+=a[i];
		if(b>0)
		cout<<"+";
		if(b<0)
		cout<<"-";
		if(b==0)
		{
			if(flag==0)
			cout<<"0";
			if(flag>0)
			cout<<"+";
			if(flag<0)
			cout<<"-";
		}
		if(b%2!=0)
		flag+=1.0*b/2.0-(b/2);
		b/=2;
	}
	return 0;
}

M Painter

题目描述：

在这里插入图片描述

解题思路：

按照题目所给要求一步一步求解，按要求输出

解题代码：

#include<bits/stdc++.h>
using namespace std;
struct CR
{
	int x,y;
	int flag;
	char ch;
	int x1,y1;
	int r;
}d[2010];
# define int long long
# define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
int Cir(int a,int b,int c,int d,int e);
int Rec(int a,int b,int c,int d,int e,int f);
signed main()
{
	IOS
	int n,m=0;
	cin>>n;
	while(n--)
	{
		
		string s;
		cin>>s;
		if(s=="Circle")
		{
			cin>>d[m].x>>d[m].y>>d[m].r;
			d[m].flag=1;
			cin>>d[m].ch;
			m++;
		}
		else if(s=="Rectangle")
		{
			cin>>d[m].x>>d[m].y>>d[m].x1>>d[m].y1;
			d[m].flag=2;
			cin>>d[m].ch;
			m++;
		}
		else
		{
			int x3,x4,y3,y4;
			cin>>x3>>y3>>x4>>y4;
			for(int i=y4; i>=y3; i--)
			{
				for(int j=x3; j<=x4; j++)
				{
					char p='.';
					for(int k=m-1;k>=0;k--)
					{
						if(d[k].flag==1)
						{
							if(Cir(j,i,d[k].x,d[k].y,d[k].r))
							{
								p=d[k].ch;
							break;
							}
							
						}
						else if(d[k].flag==2)
						{
							if(Rec(j,i,d[k].x,d[k].x1,d[k].y,d[k].y1))
							{
								p=d[k].ch;
							break;
							}
						}
						
					}
					cout<<p;
				}
				cout<<endl;
			}
		}
	}
	return 0;
} 
int Cir(int a,int b,int c,int d,int e)
{
	if((c-a)*(c-a)+(d-b)*(d-b)<=e*e)
	return 1;
	return 0;
}
int Rec(int a,int b,int c,int d,int e,int f)
{
	if(a>=c&&a<=d&&b>=e&&b<=f)
	return 1;
	return 0;
}

L Palm Island

题目描述：

在这里插入图片描述

解题思路：

冒泡排序思想，将其相对位置调整为与给出数列一致，不一致则用2调整。

解题代码：

#include <bits/stdc++.h>
#define int long long 
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
using namespace std;
const int N =1e5;
int a[N],b[N],d[N];
signed main ()
{
	IOS
	int t;
	cin>>t;
	while(t--)
	{
	int n;
	cin>>n;
	for (int i=1;i<=n;i++) 
	cin>>a[i];
	for (int i=1;i<=n;i++) 
	{
		cin>>b[i];
		d[b[i]]=i;
	}
	for (int i=1;i<=n;i++)
	{
		for (int j=1;j<n;j++)
		{
			if (d[a[j]]>d[a[j+1]])
			{
				cout<<"2";	
				swap(a[j],a[j+1]);
			}
			else 
			cout<<"1";
		}
		cout<<"1";
	}
	cout<<endl;
}
return 0;
}