目录
五、611. 有效三角形的个数 - 力扣(LeetCode)
六、 LCR 179. 查找总价格为目标值的两个商品 - 力扣(LeetCode)
一、283. 移动零 - 力扣(LeetCode)

1. 问题分析
目标:将数组中的所有
0移动到末尾,同时保持非零元素的相对顺序。示例:
输入:
[0, 1, 0, 3, 12]输出:
[1, 3, 12, 0, 0]2. 算法思路
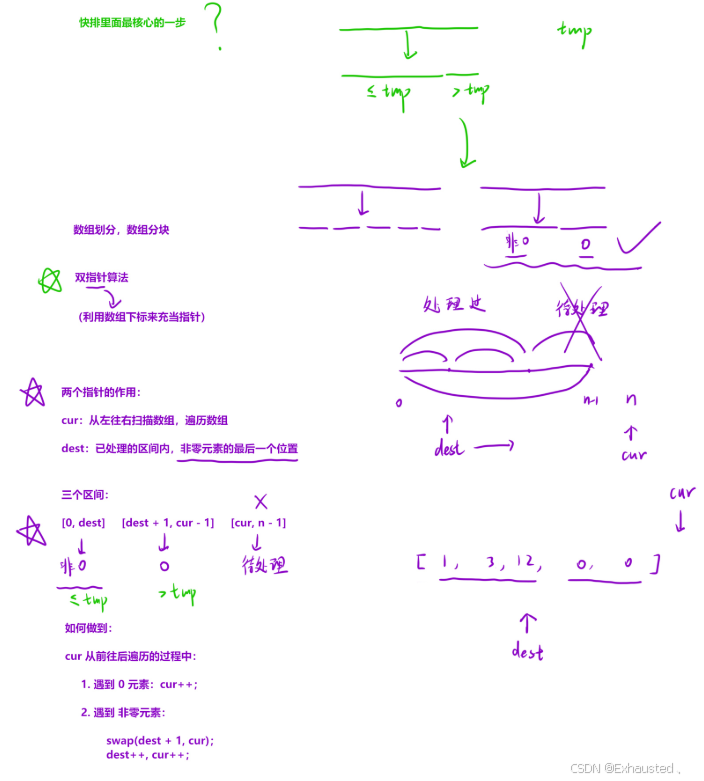
核心思想:使用双指针技术,一个指针(
cur)用于遍历数组,另一个指针(dest)用于指向当前可以放置非零元素的位置。具体步骤:
初始化
dest = -1,表示当前还没有非零元素。遍历数组,用
cur指针检查每个元素:
如果当前元素
nums[cur]是非零值:
将
dest向右移动一位(dest++),表示有一个新的非零元素可以放置。将
nums[cur]和nums[dest]交换,将非零值放到dest的位置。移动
cur指针继续遍历。如果当前元素
nums[cur]是0:
直接移动
cur指针,跳过0。遍历结束后,所有非零元素都被移动到数组的前面,而
0被留在了后面。3. 代码逐行解析
class Solution { public: void moveZeroes(vector<int>& nums) { int cur = 0, dest = -1; // 初始化 cur 和 dest while (cur < nums.size()) { // 遍历数组 if (nums[cur]) { // 如果当前元素是非零值 dest++; // dest 向右移动 swap(nums[cur], nums[dest]); // 将非零值交换到 dest 的位置 cur++; // 移动 cur 指针 } else { // 如果当前元素是 0 cur++; // 直接移动 cur 指针 } } } };
cur指针:用于遍历数组,检查每个元素。dest指针:指向当前可以放置非零元素的位置。swap(nums[cur], nums[dest]):将非零值交换到dest的位置,确保非零值的相对顺序不变。
4. 示例运行
以输入
[0, 1, 0, 3, 12]为例:
初始状态:
cur = 0,dest = -1,数组为[0, 1, 0, 3, 12]。
cur = 0,nums[0] = 0,跳过,cur++。
cur = 1,nums[1] = 1,dest++(dest = 0),交换nums[1]和nums[0],数组变为[1, 0, 0, 3, 12],cur++。
cur = 2,nums[2] = 0,跳过,cur++。
cur = 3,nums[3] = 3,dest++(dest = 1),交换nums[3]和nums[1],数组变为[1, 3, 0, 0, 12],cur++。
cur = 4,nums[4] = 12,dest++(dest = 2),交换nums[4]和nums[2],数组变为[1, 3, 12, 0, 0],cur++。遍历结束,结果为
[1, 3, 12, 0, 0]。5. 时间复杂度与空间复杂度
时间复杂度:O(n),其中
n是数组的长度。每个元素最多被遍历一次。空间复杂度:O(1),只使用了常数级别的额外空间。
6. 总结
这段代码通过双指针技术,高效地将数组中的
0移动到末尾,同时保持了非零元素的相对顺序。其核心思想是利用dest指针记录非零元素的位置,并通过交换操作将非零值逐步移动到数组的前面。
二、1089. 复写零 - 力扣(LeetCode)

1. 问题分析
目标:在数组中复制每个
0,并将后续元素向右移动。如果数组空间不足,则丢弃超出部分。示例:
输入:
[1, 0, 2, 3, 0, 4, 5, 0]输出:
[1, 0, 0, 2, 3, 0, 0, 4]2. 算法思路
核心思想:使用双指针技术,分为两个阶段:
模拟阶段:计算复制
0后的数组长度,确定有效范围。填充阶段:从后向前填充数组,复制
0并移动元素。具体步骤:
模拟阶段:
使用
cur指针遍历数组,dest指针记录复制0后的位置。如果当前元素
arr[cur]是0,则dest增加 2(因为需要复制一个0)。如果当前元素
arr[cur]不是0,则dest增加 1。当
dest达到或超过数组长度n-1时,停止模拟。边界处理:
如果
dest恰好等于n,说明最后一个元素需要被丢弃(因为复制0会导致数组越界)。将数组最后一个元素设置为
0,并调整cur和dest指针。填充阶段:
从后向前遍历数组,根据
cur指针的值填充dest指针的位置。如果
arr[cur]是0,则复制两个0。如果
arr[cur]不是0,则直接复制该值。
3. 代码逐行解析
class Solution { public: void duplicateZeros(vector<int>& arr) { int cur = 0, dest = -1, n = arr.size(); // 初始化 cur 和 dest // 模拟阶段:计算 dest 的最终位置 while (cur < n) { if (arr[cur]) dest++; // 当前元素不是 0,dest 增加 1 else dest += 2; // 当前元素是 0,dest 增加 2 if (dest >= n - 1) break; // 如果 dest 达到或超过数组长度,停止模拟 cur++; } // 边界处理:如果 dest 超出数组长度,丢弃最后一个元素 if (dest == n) { arr[n - 1] = 0; // 将最后一个元素设置为 0 cur--; // 回退 cur 指针 dest -= 2; // 回退 dest 指针 } // 填充阶段:从后向前填充数组 while (cur >= 0) { if (arr[cur]) arr[dest--] = arr[cur--]; // 当前元素不是 0,直接复制 else { arr[dest--] = 0; // 当前元素是 0,复制两个 0 arr[dest--] = 0; cur--; } } } };4. 示例运行
以输入
[1, 0, 2, 3, 0, 4, 5, 0]为例:
模拟阶段:
cur = 0,arr[0] = 1,dest = 0。
cur = 1,arr[1] = 0,dest = 2。
cur = 2,arr[2] = 2,dest = 3。
cur = 3,arr[3] = 3,dest = 4。
cur = 4,arr[4] = 0,dest = 6。
cur = 5,arr[5] = 4,dest = 7。
cur = 6,arr[6] = 5,dest = 8(超过数组长度,停止模拟)。边界处理:
dest = 8超出数组长度,将arr[7]设置为0,并调整cur = 5,dest = 6。填充阶段:
cur = 5,arr[5] = 4,arr[6] = 4,dest = 5。
cur = 4,arr[4] = 0,arr[5] = 0,arr[4] = 0,dest = 3。
cur = 3,arr[3] = 3,arr[3] = 3,dest = 2。
cur = 2,arr[2] = 2,arr[2] = 2,dest = 1。
cur = 1,arr[1] = 0,arr[1] = 0,arr[0] = 0,dest = -1。
cur = 0,arr[0] = 1,arr[0] = 1,dest = -2。最终结果:
[1, 0, 0, 2, 3, 0, 0, 4]。5. 时间复杂度与空间复杂度
时间复杂度:O(n),其中
n是数组的长度。每个元素最多被遍历两次。空间复杂度:O(1),只使用了常数级别的额外空间。
6. 总结
这段代码通过双指针技术,高效地实现了在数组中复制
0的功能。其核心思想是:
模拟阶段:计算复制
0后的数组长度,确定有效范围。填充阶段:从后向前填充数组,确保复制
0的同时不覆盖未处理的元素。这种方法避免了额外的空间开销,同时保持了较高的效率。
三、202. 快乐数 - 力扣(LeetCode)

1. 问题分析
目标:判断一个整数
n是否是快乐数。快乐数的定义:
对于一个正整数,计算其每个位置上的数字的平方和。
重复这个过程,如果最终结果为
1,则是快乐数。如果进入一个不包含
1的循环,则不是快乐数。示例:
输入:
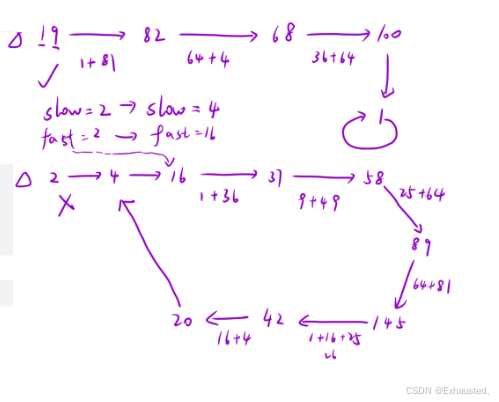
19计算过程:
1² + 9² = 82
8² + 2² = 68
6² + 8² = 100
1² + 0² + 0² = 1
输出:
true2. 算法思路
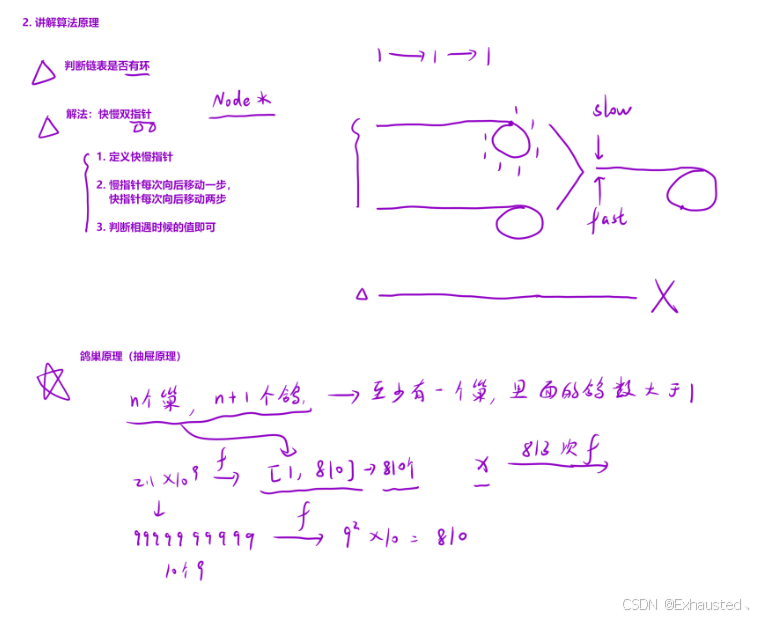
核心思想:使用快慢指针技术检测循环。
如果
n是快乐数,最终会收敛到1。如果
n不是快乐数,会进入一个循环。具体步骤:
定义一个辅助函数
Sum,用于计算一个整数的每个位置上的数字的平方和。使用快慢指针技术:
slow指针每次计算一次平方和。
fast指针每次计算两次平方和。如果
fast和slow相遇,说明存在循环。如果相遇时的值为
1,则n是快乐数;否则,不是快乐数。3. 代码逐行解析
class Solution { public: // 辅助函数:计算一个整数的每个位置上的数字的平方和 int Sum(int n) { int sum = 0; while (n) { int tmp = n % 10; // 取最后一位数字 sum += tmp * tmp; // 计算平方并累加 n = n / 10; // 去掉最后一位数字 } return sum; } // 判断一个整数是否是快乐数 bool isHappy(int n) { int slow = n; // 慢指针 int fast = Sum(n); // 快指针 while (fast != slow) { // 快慢指针未相遇时继续循环 slow = Sum(slow); // 慢指针每次计算一次平方和 fast = Sum(Sum(fast)); // 快指针每次计算两次平方和 } return slow == 1; // 如果相遇时的值为 1,则是快乐数 } };4. 示例运行
以输入
19为例:
初始状态:
slow = 19,fast = Sum(19) = 82。第一次循环:
slow = Sum(19) = 82。
fast = Sum(Sum(82)) = Sum(68) = 100。第二次循环:
slow = Sum(82) = 68。
fast = Sum(Sum(100)) = Sum(1) = 1。第三次循环:
slow = Sum(68) = 100。
fast = Sum(Sum(1)) = Sum(1) = 1。第四次循环:
slow = Sum(100) = 1。
fast = Sum(Sum(1)) = Sum(1) = 1。循环结束,
slow == 1,返回true。5. 时间复杂度与空间复杂度
时间复杂度:O(log n),其中
n是输入的整数。每次计算平方和的时间复杂度为 O(log n),快慢指针的循环次数也与n的位数相关。空间复杂度:O(1),只使用了常数级别的额外空间。
6. 总结
这段代码通过快慢指针技术,高效地判断一个整数是否是快乐数。其核心思想是:
快慢指针检测循环:通过快慢指针的移动,判断是否存在循环。
辅助函数计算平方和:通过
Sum函数计算整数的每个位置上的数字的平方和。这种方法避免了额外的空间开销,同时保持了较高的效率。
四、11. 盛最多水的容器 - 力扣(LeetCode)

1. 问题分析
目标:在数组
height中找到两条垂直线,使得它们与 x 轴构成的容器可以容纳最多的水。容器的容量:由两条垂直线之间的距离(宽度)和较短垂直线的高度决定,即
容量 = 宽度 * 高度。示例:
输入:
height = [1, 8, 6, 2, 5, 4, 8, 3, 7]输出:
49解释:选择第 2 条线(高度为 8)和第 9 条线(高度为 7),容量为
(9-2) * min(8, 7) = 7 * 7 = 49。2. 算法思路
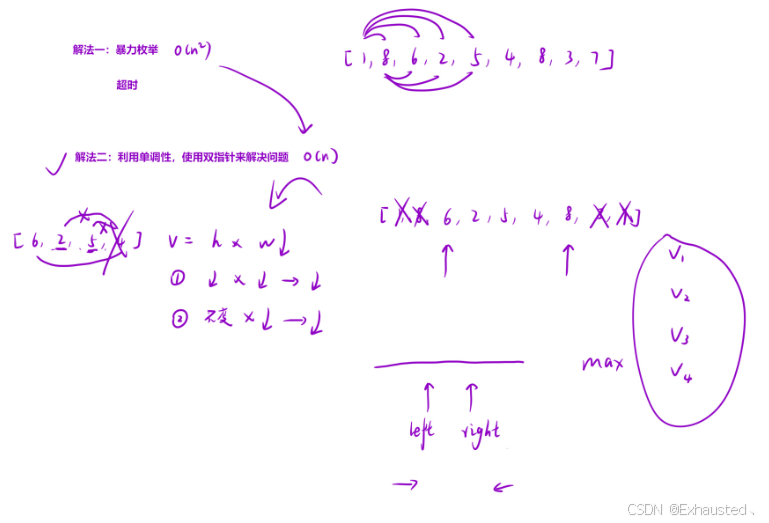
核心思想:使用双指针技术,从数组的两端向中间移动,逐步缩小搜索范围。
具体步骤:
初始化两个指针
left和right,分别指向数组的起始位置和末尾位置。计算当前容器的容量
v = (right - left) * min(height[left], height[right])。更新最大容量
tmp = max(tmp, v)。移动指针:
如果
height[left] < height[right],则移动left指针(因为容器的容量受限于较短的高度,移动较短的指针可能会找到更高的垂直线)。否则,移动
right指针。重复上述步骤,直到
left和right相遇。返回最大容量
tmp。3. 代码逐行解析
class Solution { public: int maxArea(vector<int>& height) { int left = 0; // 左指针 int right = height.size() - 1; // 右指针 int v = 0; // 当前容器的容量 int tmp = 0; // 最大容量 while (left < right) { // 双指针未相遇时继续循环 if (height[left] < height[right]) { // 左指针高度较小 v = (right - left) * height[left]; // 计算当前容量 tmp = max(tmp, v); // 更新最大容量 left++; // 移动左指针 } else { // 右指针高度较小或相等 v = (right - left) * height[right]; // 计算当前容量 tmp = max(tmp, v); // 更新最大容量 right--; // 移动右指针 } } return tmp; // 返回最大容量 } };4. 示例运行
以输入
height = [1, 8, 6, 2, 5, 4, 8, 3, 7]为例:
初始状态:
left = 0,right = 8,tmp = 0。第一次循环:
height[left] = 1,height[right] = 7。计算容量
v = (8 - 0) * 1 = 8。更新
tmp = max(0, 8) = 8。移动
left指针,left = 1。第二次循环:
height[left] = 8,height[right] = 7。计算容量
v = (8 - 1) * 7 = 49。更新
tmp = max(8, 49) = 49。移动
right指针,right = 7。第三次循环:
height[left] = 8,height[right] = 3。计算容量
v = (7 - 1) * 3 = 18。更新
tmp = max(49, 18) = 49。移动
right指针,right = 6。第四次循环:
height[left] = 8,height[right] = 8。计算容量
v = (6 - 1) * 8 = 40。更新
tmp = max(49, 40) = 49。移动
left指针,left = 2。循环结束,返回
tmp = 49。5. 时间复杂度与空间复杂度
时间复杂度:O(n),其中
n是数组的长度。双指针最多遍历数组一次。空间复杂度:O(1),只使用了常数级别的额外空间。
6. 总结
这段代码通过双指针技术,高效地解决了盛最多水的容器问题。其核心思想是:
双指针缩小搜索范围:通过移动较短的指针,逐步缩小搜索范围,确保不漏掉可能的更大容量。
容量计算:根据两条垂直线之间的距离和较短的高度计算容量。
这种方法避免了暴力搜索的高时间复杂度(O(n^2)),将问题优化为线性时间复杂度。
五、611. 有效三角形的个数 - 力扣(LeetCode)

1. 问题分析
目标:在数组
nums中找到所有满足三角形条件的三元组(nums[i], nums[j], nums[k]),即nums[i] + nums[j] > nums[k]、nums[i] + nums[k] > nums[j]和nums[j] + nums[k] > nums[i]。三角形条件:对于任意三条边,较短的两条边之和必须大于第三条边。
示例:
输入:
nums = [2, 2, 3, 4]输出:
3解释:有效的三元组为
(2, 3, 4)、(2, 3, 4)和(2, 2, 3)。2. 算法思路
核心思想:利用排序和双指针技术,将问题转化为固定最长边,然后在剩余部分中寻找满足条件的两条较短边。
具体步骤:
排序:将数组
nums排序,方便后续操作。固定最长边:从数组的末尾开始,依次固定最长边
nums[i]。双指针查找:
使用双指针
left和right,分别指向数组的起始位置和最长边的左侧位置。如果
nums[left] + nums[right] > nums[i],则说明从left到right-1的所有元素都可以与nums[right]和nums[i]组成有效三角形,因此累加right - left到结果中,并移动right指针。否则,移动
left指针,尝试找到更大的较短边。重复上述步骤,直到所有最长边都被处理完毕。
3. 代码逐行解析
class Solution { public: int triangleNumber(vector<int>& nums) { sort(nums.begin(), nums.end()); // 对数组进行排序 int sum = 0; // 统计有效三角形的个数 int n = nums.size(); // 数组的长度 for (int i = n - 1; i >= 2; i--) { // 固定最长边 nums[i] int left = 0; // 左指针 int right = i - 1; // 右指针 while (left < right) { // 双指针未相遇时继续循环 if (nums[left] + nums[right] > nums[i]) { // 满足三角形条件 sum += (right - left); // 累加有效三角形的个数 right--; // 移动右指针 } else { // 不满足三角形条件 left++; // 移动左指针 } } } return sum; // 返回有效三角形的个数 } };4. 示例运行
以输入
nums = [2, 2, 3, 4]为例:
排序后数组:
[2, 2, 3, 4]。固定最长边
nums[3] = 4:
left = 0,right = 2。
nums[left] + nums[right] = 2 + 3 = 5 > 4,满足条件,累加right - left = 2到sum,sum = 2。移动
right指针,right = 1。
nums[left] + nums[right] = 2 + 2 = 4 <= 4,不满足条件,移动left指针,left = 1。循环结束。
固定最长边
nums[2] = 3:
left = 0,right = 1。
nums[left] + nums[right] = 2 + 2 = 4 > 3,满足条件,累加right - left = 1到sum,sum = 3。移动
right指针,right = 0。循环结束。
返回结果:
sum = 3。5. 时间复杂度与空间复杂度
时间复杂度:O(n^2),其中
n是数组的长度。排序的时间复杂度为 O(n log n),双指针的循环时间复杂度为 O(n^2)。空间复杂度:O(1),只使用了常数级别的额外空间。
6. 总结
这段代码通过排序和双指针技术,高效地解决了有效三角形的个数问题。其核心思想是:
排序:将数组排序,方便固定最长边。
双指针查找:固定最长边后,使用双指针在剩余部分中寻找满足条件的两条较短边。
这种方法避免了暴力搜索的高时间复杂度(O(n^3)),将问题优化为 O(n^2) 的时间复杂度。
六、 LCR 179. 查找总价格为目标值的两个商品 - 力扣(LeetCode)

1. 问题分析
目标:在有序数组
price中找到两个数,使它们的和等于target。输入:
price:一个升序排列的整数数组。
target:目标值。输出:返回两个数的值,如果不存在这样的两个数,则返回
{-1, -1}。示例:
输入:
price = [2, 7, 11, 15],target = 9输出:
[2, 7]2. 算法思路
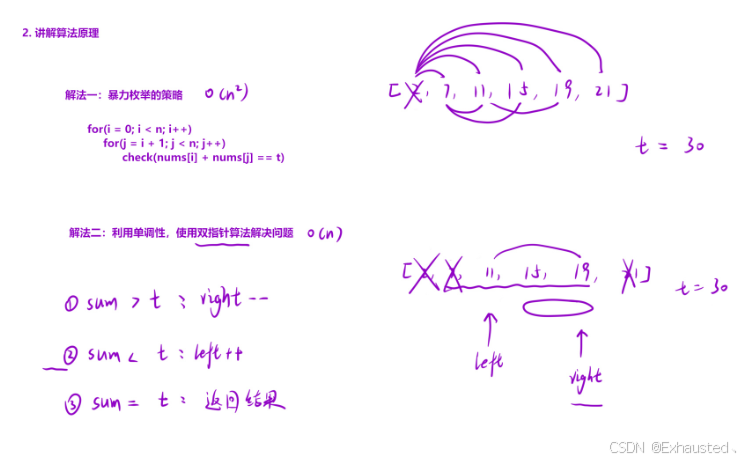
核心思想:利用数组的有序性,使用双指针技术从数组的两端向中间移动,逐步缩小搜索范围。
具体步骤:
初始化两个指针
left和right,分别指向数组的起始位置和末尾位置。计算当前两个指针指向的数的和
sum = price[left] + price[right]。比较
sum与target:
如果
sum > target,说明当前和过大,需要减小和,因此将right指针左移。如果
sum < target,说明当前和过小,需要增大和,因此将left指针右移。如果
sum == target,说明找到了满足条件的两个数,直接返回它们的值。重复上述步骤,直到
left和right指针相遇。如果未找到满足条件的两个数,返回
{-1, -1}。3. 代码逐行解析
class Solution { public: vector<int> twoSum(vector<int>& price, int target) { int left = 0; // 左指针,指向数组的起始位置 int right = price.size() - 1; // 右指针,指向数组的末尾位置 while (left < right) { // 双指针未相遇时继续循环 int sum = price[left] + price[right]; // 计算当前两个数的和 if (sum > target) { // 如果和大于目标值 right--; // 右指针左移,减小和 } else if (sum < target) { // 如果和小于目标值 left++; // 左指针右移,增大和 } else { // 如果和等于目标值 return {price[left], price[right]}; // 返回满足条件的两个数 } } return {-1, -1}; // 如果未找到,返回 {-1, -1} } };4. 示例运行
以输入
price = [2, 7, 11, 15],target = 9为例:
初始状态:
left = 0,right = 3。
price[left] = 2,price[right] = 15。第一次循环:
sum = 2 + 15 = 17。
sum > target,右指针左移,right = 2。第二次循环:
sum = 2 + 11 = 13。
sum > target,右指针左移,right = 1。第三次循环:
sum = 2 + 7 = 9。
sum == target,返回[2, 7]。5. 时间复杂度与空间复杂度
时间复杂度:O(n),其中
n是数组的长度。双指针最多遍历数组一次。空间复杂度:O(1),只使用了常数级别的额外空间。
6. 总结
这段代码通过双指针技术,高效地解决了有序数组中的两数之和问题。其核心思想是:
利用有序性:通过数组的有序性,快速缩小搜索范围。
双指针移动:根据当前和与目标值的大小关系,决定移动哪个指针。
这种方法避免了暴力搜索的高时间复杂度(O(n^2)),将问题优化为线性时间复杂度。
七、15. 三数之和 - 力扣(LeetCode)

1. 问题分析
目标:在数组
nums中找到所有满足nums[i] + nums[j] + nums[k] = 0的三元组,且三元组不重复。输入:一个整数数组
nums。输出:所有满足条件的三元组,存储在
vector<vector<int>>中。示例:
输入:
nums = [-1, 0, 1, 2, -1, -4]输出:
[[-1, -1, 2], [-1, 0, 1]]2. 算法思路
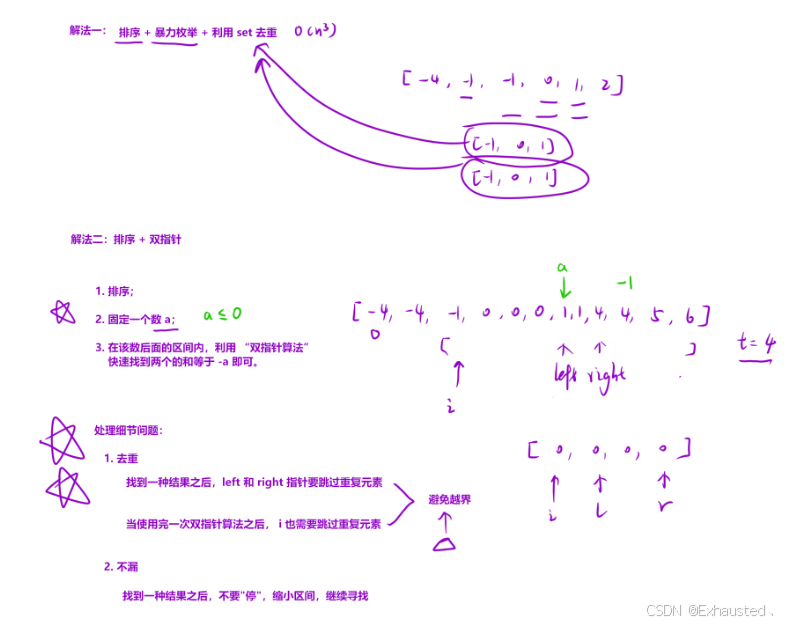
核心思想:利用排序和双指针技术,将三数之和问题转化为两数之和问题。
具体步骤:
排序:将数组
nums排序,方便后续操作。固定第一个数:遍历数组,固定第一个数
nums[i]。
如果
nums[i] > 0,则直接退出循环(因为数组已排序,后面的数都大于 0,无法满足三数之和为 0)。双指针查找:
使用双指针
left和right,分别指向i+1和n-1。计算目标值
target = -nums[i],即nums[left] + nums[right] = target。如果
nums[left] + nums[right] == target,则找到一个满足条件的三元组,将其加入结果集,并移动left和right指针。如果
nums[left] + nums[right] > target,则移动right指针。如果
nums[left] + nums[right] < target,则移动left指针。去重操作:
在固定第一个数
nums[i]时,跳过重复的值。在找到满足条件的三元组后,跳过
left和right指针指向的重复值。返回结果:最终返回所有满足条件的三元组。
3. 代码逐行解析
class Solution { public: vector<vector<int>> threeSum(vector<int>& nums) { sort(nums.begin(), nums.end()); // 对数组进行排序 int n = nums.size(); // 数组的长度 vector<vector<int>> ret; // 存储结果的三元组 for (int i = 0; i < n;) { // 固定第一个数 nums[i] if (nums[i] > 0) break; // 如果 nums[i] > 0,直接退出循环 int left = i + 1; // 左指针 int right = n - 1; // 右指针 int target = -nums[i]; // 目标值 while (left < right) { // 双指针未相遇时继续循环 if (nums[left] + nums[right] == target) { // 找到满足条件的三元组 ret.push_back({nums[i], nums[left], nums[right]}); // 加入结果集 left++, right--; // 移动指针 // 去重操作:跳过 left 和 right 指向的重复值 while (left < right && nums[left] == nums[left - 1]) left++; while (left < right && nums[right] == nums[right + 1]) right--; } else if (nums[left] + nums[right] > target) { // 和大于目标值 right--; // 移动右指针 // 去重操作:跳过 right 指向的重复值 if ((left < right) && (nums[right] == nums[right + 1])) right--; } else { // 和小于目标值 left++; // 移动左指针 // 去重操作:跳过 left 指向的重复值 if ((left < right) && (nums[left] == nums[left - 1])) left++; } } i++; // 移动固定数的指针 // 去重操作:跳过 i 指向的重复值 while ((i < n) && (nums[i] == nums[i - 1])) i++; } return ret; // 返回结果 } };4. 示例运行
以输入
nums = [-1, 0, 1, 2, -1, -4]为例:
排序后数组:
[-4, -1, -1, 0, 1, 2]。固定第一个数
nums[0] = -4:
left = 1,right = 5。
target = 4。
nums[left] + nums[right] = -1 + 2 = 1 < 4,移动left指针。
left = 2,nums[left] + nums[right] = -1 + 2 = 1 < 4,移动left指针。
left = 3,nums[left] + nums[right] = 0 + 2 = 2 < 4,移动left指针。
left = 4,nums[left] + nums[right] = 1 + 2 = 3 < 4,移动left指针。循环结束。
固定第一个数
nums[1] = -1:
left = 2,right = 5。
target = 1。
nums[left] + nums[right] = -1 + 2 = 1 == target,找到三元组[-1, -1, 2],加入结果集。移动
left和right指针,left = 3,right = 4。
nums[left] + nums[right] = 0 + 1 = 1 == target,找到三元组[-1, 0, 1],加入结果集。移动
left和right指针,left = 4,right = 3,循环结束。固定第一个数
nums[2] = -1:
跳过重复值。
固定第一个数
nums[3] = 0:
left = 4,right = 5。
target = 0。
nums[left] + nums[right] = 1 + 2 = 3 > 0,移动right指针。循环结束。
返回结果:
[[-1, -1, 2], [-1, 0, 1]]。5. 时间复杂度与空间复杂度
时间复杂度:O(n^2),其中
n是数组的长度。排序的时间复杂度为 O(n log n),双指针的循环时间复杂度为 O(n^2)。空间复杂度:O(1),忽略结果集的空间,只使用了常数级别的额外空间。
6. 总结
这段代码通过排序和双指针技术,高效地解决了三数之和问题。其核心思想是:
排序:将数组排序,方便固定第一个数。
双指针查找:固定第一个数后,使用双指针在剩余部分中寻找满足条件的两数。
去重操作:通过跳过重复值,确保结果集中不包含重复的三元组。
这种方法避免了暴力搜索的高时间复杂度(O(n^3)),将问题优化为 O(n^2) 的时间复杂度。
1. 为什么在
nums[left] + nums[right] > target和nums[left] + nums[right] < target时使用if?当
nums[left] + nums[right] > target或nums[left] + nums[right] < target时,只需要移动指针一次,并检查当前指针指向的值是否与下一个值重复。如果重复,则再移动一次指针。使用
if的原因是:
单次移动:每次只需要移动指针一次,然后检查是否需要跳过重复值。
避免过度移动:如果使用
while,可能会导致指针移动过多,从而错过某些有效的三元组。示例
假设
nums = [-2, 0, 0, 2, 2],target = 0:
固定
nums[i] = -2,left = 1,right = 4。
nums[left] + nums[right] = 0 + 2 = 2 > target,移动right指针。
使用
if检查nums[right]是否与nums[right + 1]重复。如果重复,再移动一次
right指针。如果使用
while,可能会导致right指针直接移动到left的位置,从而错过有效的三元组。
2. 为什么在找到三元组后使用
while?当找到满足条件的三元组时,需要跳过所有连续的重复值,以确保结果中没有重复的三元组。
使用
while的原因是:
连续跳过重复值:在找到三元组后,
left和right指针指向的值可能与下一个值重复,因此需要连续跳过所有重复值。确保结果唯一:如果不使用
while,可能会导致结果中包含重复的三元组。示例
假设
nums = [-2, 0, 0, 2, 2],target = 0:
固定
nums[i] = -2,left = 1,right = 4。
nums[left] + nums[right] = 0 + 2 = 0,找到三元组[-2, 0, 2]。使用
while跳过所有连续的重复值:
left从1移动到2(跳过重复的0)。
right从4移动到3(跳过重复的2)。如果不使用
while,结果中可能会包含重复的三元组[-2, 0, 2]。
八、18. 四数之和 - 力扣(LeetCode)

1. 问题分析
目标:在数组
nums中找到所有满足nums[i] + nums[j] + nums[k] + nums[l] = target的四元组,且四元组不重复。输入:
nums:一个整数数组。
target:目标值。输出:所有满足条件的四元组,存储在
vector<vector<int>>中。示例:
输入:
nums = [1, 0, -1, 0, -2, 2],target = 0输出:
[[-2, -1, 1, 2], [-2, 0, 0, 2], [-1, 0, 0, 1]]2. 算法思路
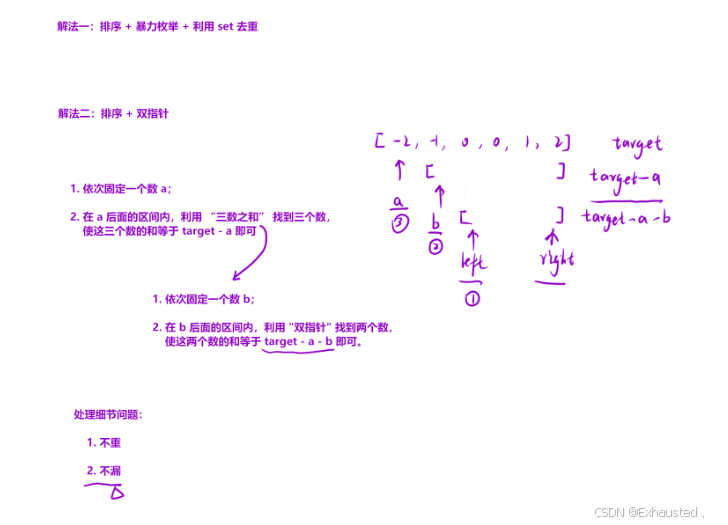
核心思想:利用排序和双指针技术,将四数之和问题转化为三数之和问题,再进一步转化为两数之和问题。
具体步骤:
排序:将数组
nums排序,方便后续操作。固定前两个数:
使用两层循环,分别固定前两个数
nums[i]和nums[j]。在固定
nums[i]和nums[j]后,问题转化为在剩余部分中找到两个数nums[left]和nums[right],使得nums[left] + nums[right] = target - nums[i] - nums[j]。双指针查找:
使用双指针
left和right,分别指向j+1和n-1。计算目标值
sum = target - nums[i] - nums[j]。如果
nums[left] + nums[right] == sum,则找到一个满足条件的四元组,将其加入结果集,并移动left和right指针。如果
nums[left] + nums[right] < sum,则移动left指针。如果
nums[left] + nums[right] > sum,则移动right指针。去重操作:
在固定
nums[i]和nums[j]时,跳过重复的值。在找到满足条件的四元组后,跳过
left和right指针指向的重复值。返回结果:最终返回所有满足条件的四元组。
3. 代码逐行解析
class Solution { public: vector<vector<int>> fourSum(vector<int>& nums, int target) { vector<vector<int>> ret; // 存储结果的四元组 sort(nums.begin(), nums.end()); // 对数组进行排序 int n = nums.size(); // 数组的长度 for (int i = 0; i < n;) { // 固定第一个数 nums[i] for (int j = i + 1; j < n;) { // 固定第二个数 nums[j] int left = j + 1; // 左指针 int right = n - 1; // 右指针 long long sum = (long long)target - nums[i] - nums[j]; // 目标值 while (left < right) { // 双指针未相遇时继续循环 int tmp = nums[left] + nums[right]; // 当前两个数的和 if (tmp < sum) { // 和小于目标值 left++; // 移动左指针 } else if (tmp > sum) { // 和大于目标值 right--; // 移动右指针 } else { // 和等于目标值 ret.push_back({nums[i], nums[j], nums[left], nums[right]}); // 加入结果集 left++, right--; // 移动指针 // 去重操作:跳过 left 和 right 指向的重复值 while (left < right && nums[left] == nums[left - 1]) left++; while (left < right && nums[right] == nums[right + 1]) right--; } } j++; // 移动第二个数的指针 // 去重操作:跳过 j 指向的重复值 while (j < n && nums[j] == nums[j - 1]) j++; } i++; // 移动第一个数的指针 // 去重操作:跳过 i 指向的重复值 while (i < n && nums[i] == nums[i - 1]) i++; } return ret; // 返回结果 } };4. 示例运行
以输入
nums = [1, 0, -1, 0, -2, 2],target = 0为例:
排序后数组:
[-2, -1, 0, 0, 1, 2]。固定第一个数
nums[0] = -2:
固定第二个数
nums[1] = -1:
left = 2,right = 5。
sum = 0 - (-2) - (-1) = 3。
nums[left] + nums[right] = 0 + 2 = 2 < 3,移动left指针。
left = 3,nums[left] + nums[right] = 0 + 2 = 2 < 3,移动left指针。
left = 4,nums[left] + nums[right] = 1 + 2 = 3 == sum,找到四元组[-2, -1, 1, 2],加入结果集。移动
left和right指针,left = 5,right = 4,循环结束。固定第二个数
nums[2] = 0:
left = 3,right = 5。
sum = 0 - (-2) - 0 = 2。
nums[left] + nums[right] = 0 + 2 = 2 == sum,找到四元组[-2, 0, 0, 2],加入结果集。移动
left和right指针,left = 4,right = 4,循环结束。固定第一个数
nums[1] = -1:
固定第二个数
nums[2] = 0:
left = 3,right = 5。
sum = 0 - (-1) - 0 = 1。
nums[left] + nums[right] = 0 + 2 = 2 > 1,移动right指针。
right = 4,nums[left] + nums[right] = 0 + 1 = 1 == sum,找到四元组[-1, 0, 0, 1],加入结果集。移动
left和right指针,left = 4,right = 3,循环结束。返回结果:
[[-2, -1, 1, 2], [-2, 0, 0, 2], [-1, 0, 0, 1]]。5. 时间复杂度与空间复杂度
时间复杂度:O(n^3),其中
n是数组的长度。排序的时间复杂度为 O(n log n),双指针的循环时间复杂度为 O(n^3)。空间复杂度:O(1),忽略结果集的空间,只使用了常数级别的额外空间。
6. 总结
这段代码通过排序和双指针技术,高效地解决了四数之和问题。其核心思想是:
排序:将数组排序,方便固定前两个数。
双指针查找:固定前两个数后,使用双指针在剩余部分中寻找满足条件的两数。
去重操作:通过跳过重复值,确保结果集中不包含重复的四元组。
这种方法避免了暴力搜索的高时间复杂度(O(n^4)),将问题优化为 O(n^3) 的时间复杂度。























 78
78

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








