我可能找到了一个新的质数有140亿位数

2024年10月，来自美国的一个网友通过计算机梅森大搜索网站，找到了一个新的质数，这个质数有41034320位数，为2的136279841次方-1。

 而距离上一次人类找到的特别大的质数过去了仅仅6年，已经超出了1600多万位。上次是M82589933（有24862048位数），这次是M136279841。

 

不过我通过M216091与M20996011，利用自己的特殊手段筛选梅森素数，便一口咬定M46694888101一定是个质数，也许现阶段的计算器无法验证它是合数还是质数，但我认为它就是质数。

 

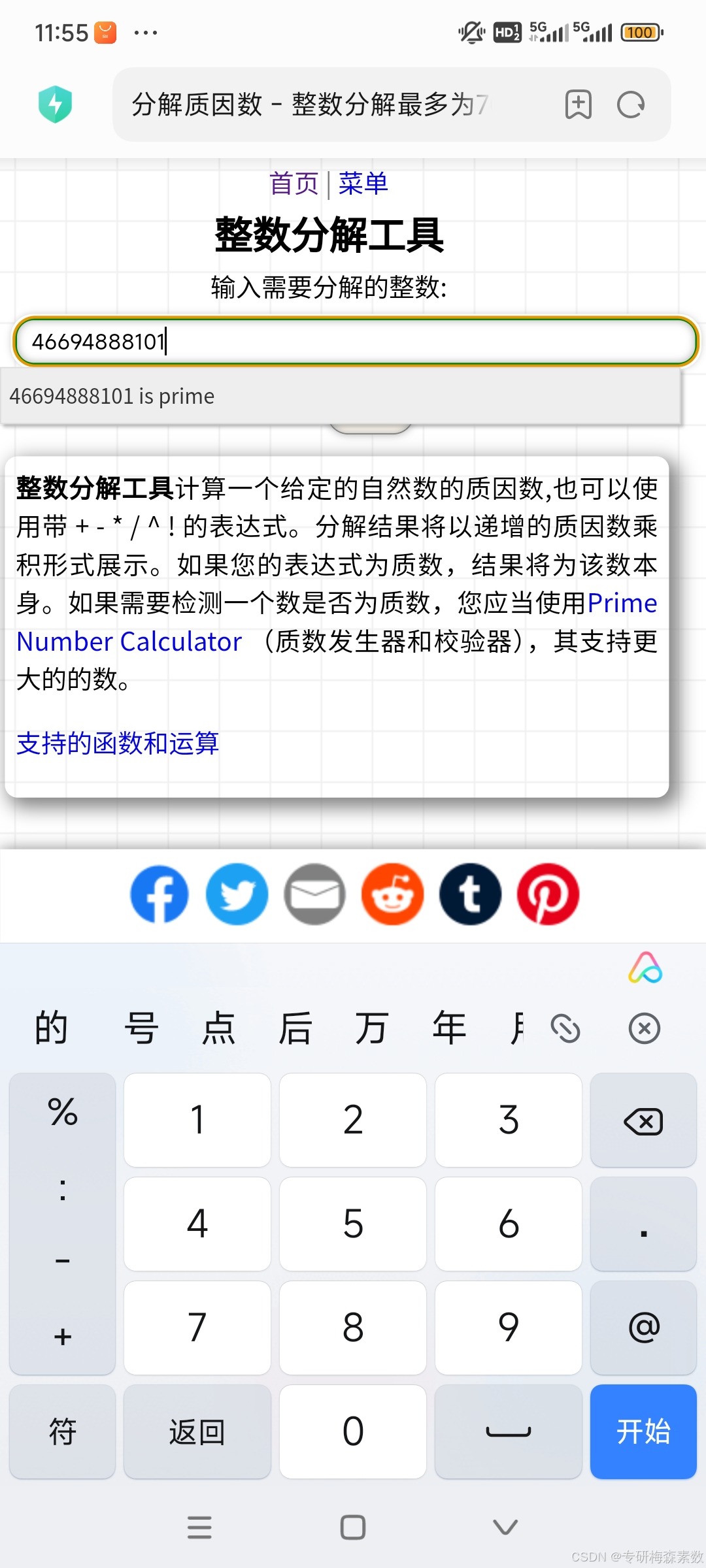
我一口咬定M46694888101（466亿多）是质数是有原因的，因为早20年前就有人利用梅森素数大搜索找到了M216091是质数，我通过216091分解质因数得到3²✖️7⁴✖️10+1

且216091✖️2-1＝41✖️83✖️127

并且后来在21世纪初有人找到M20996011是梅森素数以后，我用20996011分解质因数得到3⁴✖️7²✖️23²✖️10+1

且20996011✖️2-1＝3301✖️12721

 

如今我利用3的n次方✖️7的n次方✖️10的n次方+1，如果这个数字是质数，极大可能就是梅森素数，我用如此筛选法寻找梅森素数，虽然我不会用电脑验证，我家也没有特别大的豪华版电脑，但我用这个方式一致认为M46694888101是梅森素数。

因为466948881分解得到3⁴✖️7⁸，又因为4669488811不是质数，所以我便想通过3⁴✖️7⁸✖️10²+1看看是不是质数，果然46694888101是质数。

又因为46694888101✖️2-1正好又等于19²✖️379²✖️1801，我通过这样分解质因数以后，结合216091以及20996011，便严重怀疑了它。

 好在如今，美国做出了高额悬赏，找到超过1亿位数以上的质数，奖励15万。

最初的时候，有很多人认为M2147483647是梅森素数，后在1983年被人用电脑找到了一个素因子为2✖️68745✖️2147483647+1，

如果M46694888101经电脑验证是质数的话，我觉得我至少可以拿美国机构的150万悬赏奖励了

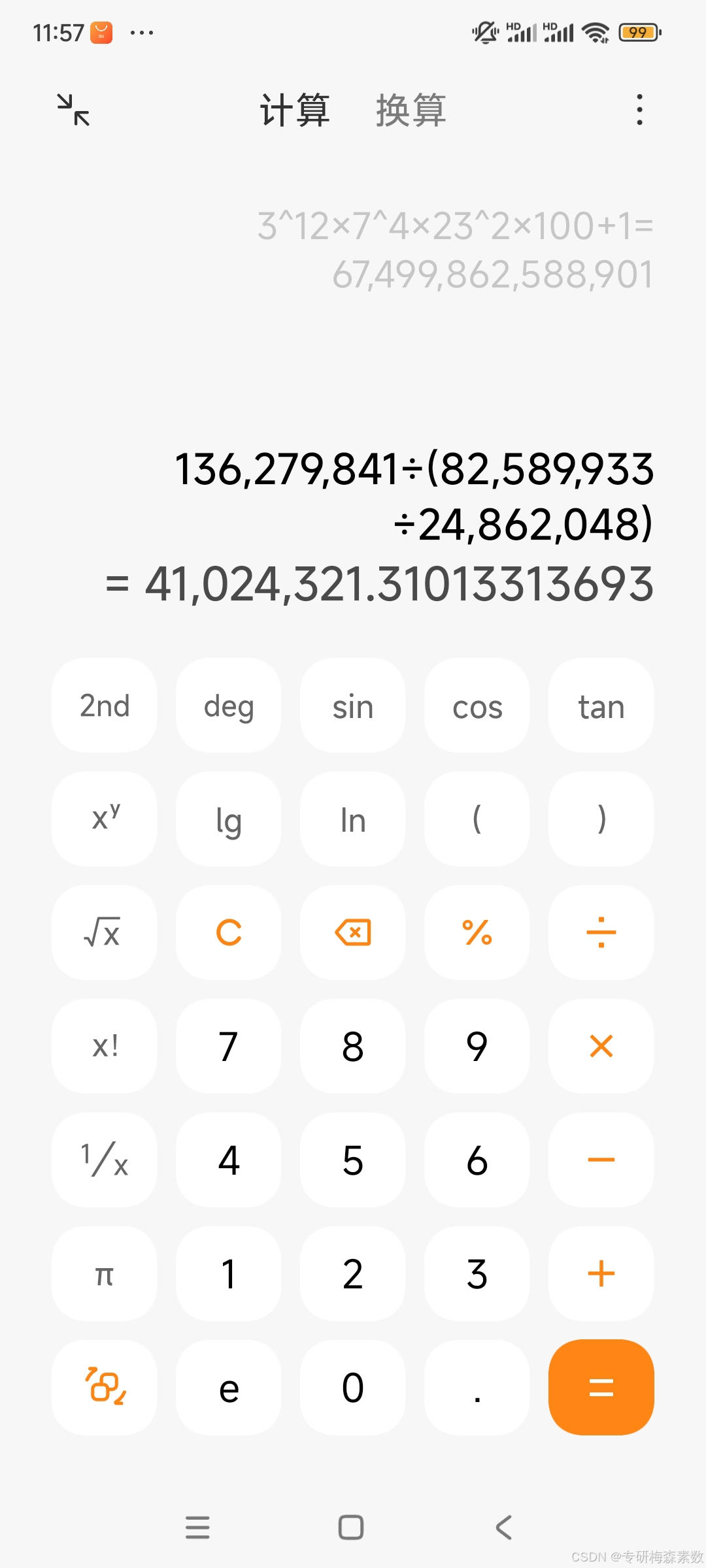
我通过M82589933得到有24862048位数以后，再通过M136279841得到有41034320位数以后，再来看一下M46694888101有多少位数？

 

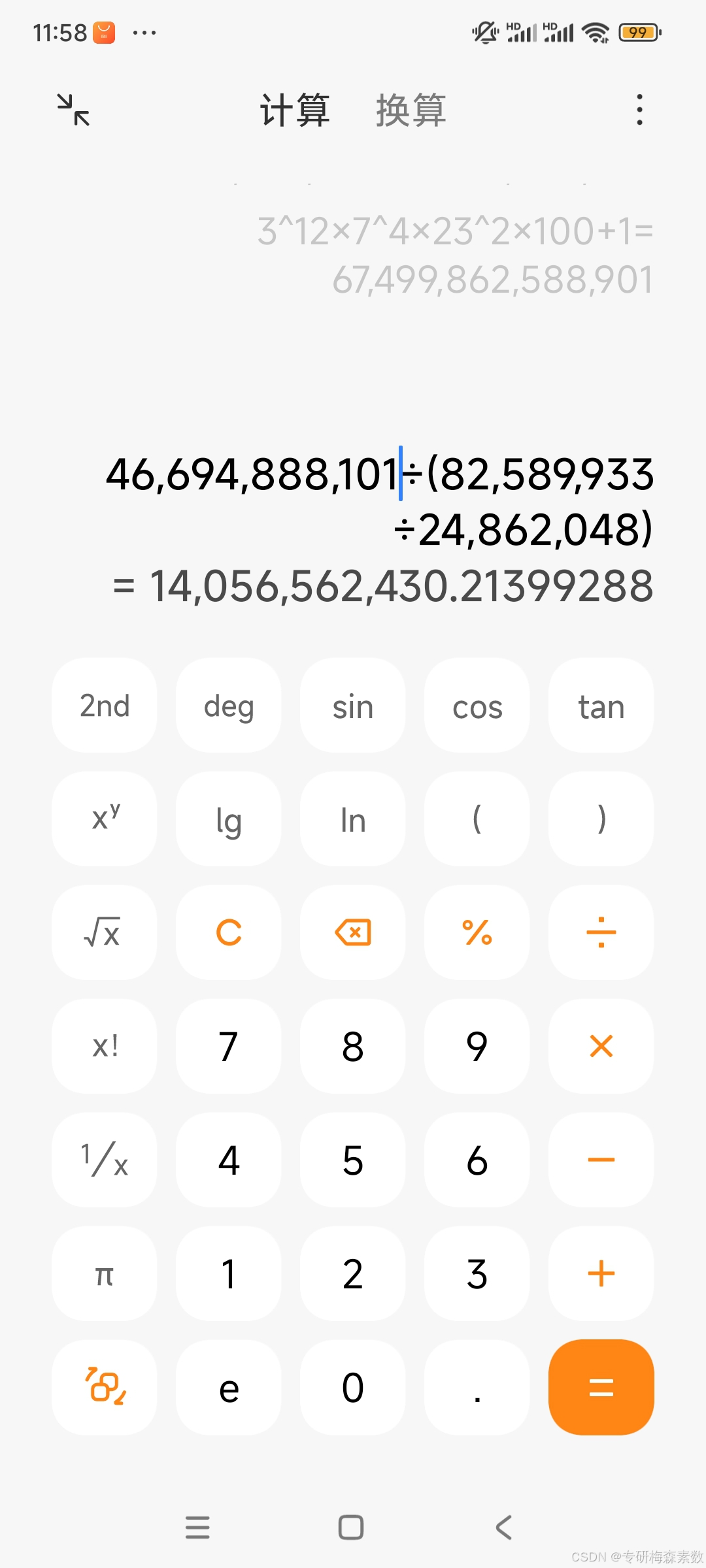
 140亿5656万2430位数，竟然高出342倍。

不知道现如今有没有专业的电脑可以用来验证我所说的2⁴⁶⁶⁹⁴⁸⁸⁸¹⁰¹-1是不是质数，如果它真的是质数，我等着国际组织奖赏我多少钱吧？