梅森素数大搜索猜测部分

最新推荐文章于 2025-04-28 09:38:40 发布
最新推荐文章于 2025-04-28 09:38:40 发布
阅读量512 收藏 8
点赞数 7
文章标签： python
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/2401_82762129/article/details/136064525
版权

当2的p次方-1是质数，首先已经证明p一定是质数。但是世界未破解的难题是，梅森素数这样的完美数字是否存在无穷多个。截止2024年，距离上一个指数82589933（24862048位数质数）已经六年过去了，至今一无所获。那么问题就来了，在指数一亿多到100亿多的范围内，罪魁祸首又藏在哪？这被誉为数学史上的珍宝。

本人经过梅森素数指数p等于21701、216091和20996011被证实为质数的时候，作出了一个猜测，因为21701＝2²✖️5²✖️7✖️31+1

216091＝2✖️5✖️3²✖️7的四次方+1

20996011＝2✖️5✖️3的四次方✖️7²✖️23²+1

通过这一类型推断发现并猜测认为，不知道这样说大家能不能听懂，规律是

在2亿-2.2亿多，20亿-22亿多，如果这个大数存在2✖️3✖️5✖️7✖️的平方，或者3次方，或者四次方，再乘以任何一个质数平方➕1，而且➕1以后是质数，那么这个数字就可以被重点关注为梅森素数。比如204575491、207532837、201924101、2382392251、2136274561、227040031

还有2063244961、2173265641也需要被重点关注

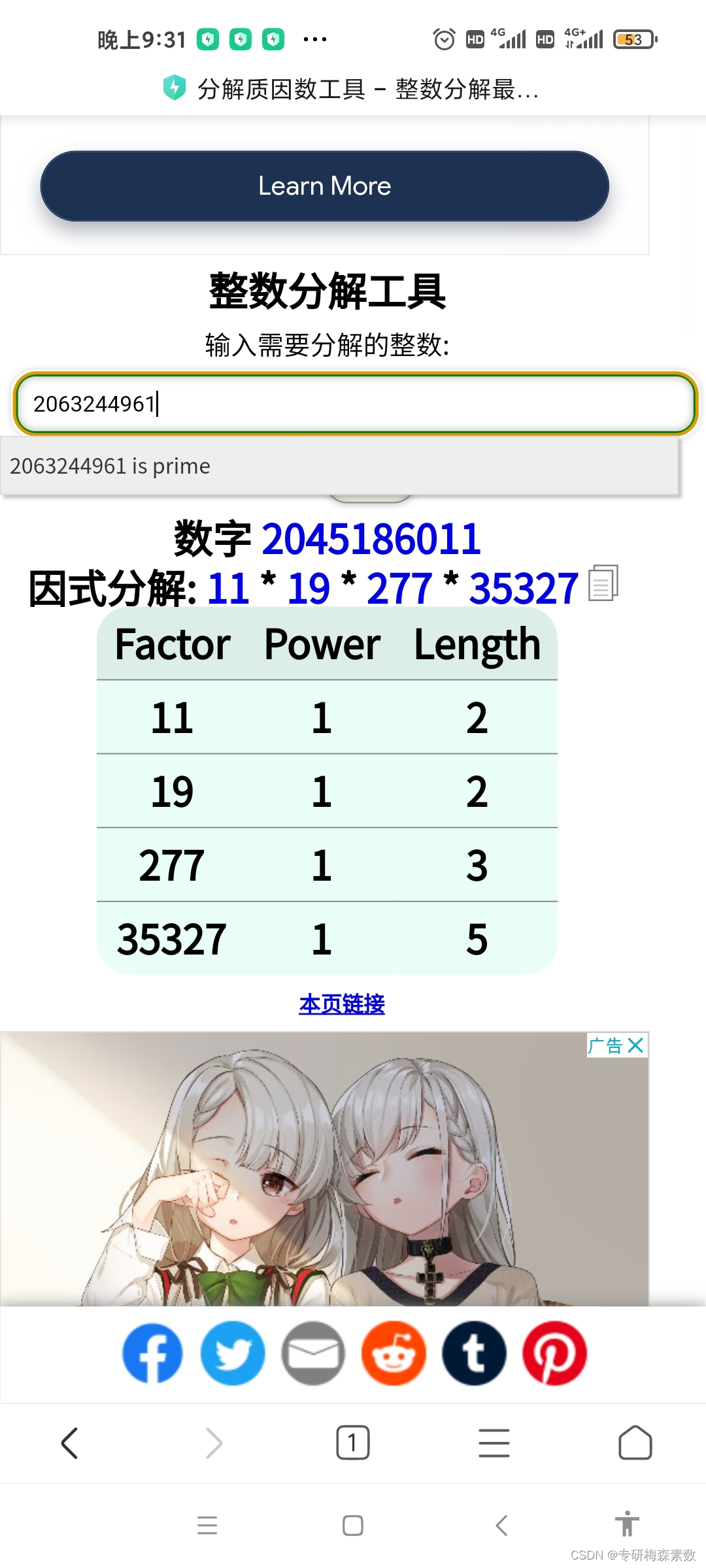
243e2daf177142049b7bc837cd9a74a2.jpg

 03d9e1a2cff7474ca2e48fe286c988f5.jpg

 然后再通过859433和82589933这一类型发现，可能是因为2的33次方等于8589934592，所以跟这个数字有关的存在的质数，也需要被着重关注，那么我在8亿多里面就列出了两个数字来作为猜测部分

835899637、858993433。

dd6ddaae9c754aee8825a5bfe98acb5f.jpg

 8983e740b5d14382946f092143a40c2a.jpg

 

程序员意外发现迄今最大素数，约25000000位
weixin_43923408的博客
12-30 411
  已知最大素数前几个数位(来源：QUARTZ) Great Internet Mersenne Prime Search(GIMPS)发现了新的最大素数：2^(82589933)-1，拥有24862048位。美国佛罗里达州的程序员 Patrick Laroche，利用GIMPS项目提供的软件，于2018年12月7日由个人电脑上自动运行的程序寻找到了迄今为止最大的梅森素数。 新的素数，也...
关于梅森素数定理(网上收集)
xiaocai0001的专栏
10-07 3580
一、梅森素数    我们把一个大于1的自然数叫作素数，如果只有1和它本身可以整除它。如果一个比1大的自然数不是素数，我们就叫它合数。1既不是素数，也不是合数。 比如说，你很容易就可以验证7是一个素数；而15是一个合数，因为除了1和15外，3和5都可以整除15。根据定义，2是一个素数，它是唯一的偶素数。早在公元前三百年的古希腊时代，伟大的数学家欧几里德就证明了存在着无穷多个素数。 关于素数，有许多既
梅森素数世界难题未解之谜
2401_82762129的博客
01-30 496
但是不是所有的指数p都能代入，这是我整理出来可以代入的p，最大值为82589933，目前已知82589933属于第4811740个质数，开根号为9087.9。梅森素数的探索非常艰巨，即使你有高深的数论知识，就连科学家也无法解释它的规律，比如82589933和77232917之间到底存在着什么？现已知两者相差294338个质数，两者之差为5357016，两者之和为159822850，两者之积为6378兆6914亿4042万4561。早先就有人已经证明过2的p次方-1若是质数，p一定就是质数，这是完全成立的。
关于2的p次方-1
2401_82762129的博客
01-23 603
第100个质数是541，第1000个质数是7919，第1亿个质数是2,038,074,743，我发现2的31次方-1等于2147483647属于第105,097,565个质数。但是2的132049次方-1是素数，这问题来了，现在有人发现2的2147483647次方-1不是素数，我预测在p＝21.4亿-21.6亿的这三千万范围内存在未发现的梅森素数p。这是我发现的梅森素数p为质数，属于第几个质数，不知道发现了前51个质数p属于第几个质数能不能通过这个找到梅森素数的分布规律。
梅森素数列表
2401_82762129的博客
01-23 798
（2的31次方-1），最后发现了一个合数，所以现在的焦点是一个39位数的（2的127次方-1）170141183460469231731687303715884105727，如果这个数字代入后依旧是合数，梅森素数是否存在无穷多个真的是个无解了。2的p次方-1，目前截止2024年1月，发现最大的梅森素数p为82589933。六年来人们都没有发现新的梅森素数，但之前着重通过双梅规律来着重关注的是2147483647。
梅森素数指数p与相邻数的关系
2401_82762129的博客
01-30 408
我从20多万和2000多万里面都发现了这样神奇的分解，而且都有2✖️3✖️5✖️7，这样不难看出在2亿多跟20多亿的时候，如果有这样用2✖️5✖️7再乘以100以内的质数开平方，然后试试+1，如果这个数字加上去是质数，且减去1能分解为类似有公因数2、3、5、7，这四个数随便怎么开平方立方，再乘以一个质数开平方，试一试弄到指数里面会不会成为新发现的梅森素数。指数21701分解为7✖️31✖️100+1。且1449被分解为3✖️3✖️7✖️23。且147被分解为3✖️7✖️7。
程序员的数学思维修炼（趣味解读）梅森素数
weixin_45892228的博客
10-14 1194
梅森在欧几里得、费马等人的有关研究的基础上对2P－1作了大量的计算、验证 工作，并于1644年在他的《物理数学随感》一书中断言：对于P＝2 、3 、5 、7 、13 、17、 19 、31 、67 、127 、257时，2P－1是素数；我们知道，在自然数中素数较少，10000以内的自然数中只有1229个素数，而孪生素 数就更少，10000以内的孪生素数只有205对 (510个)。当P＝2 、3 、5 、7时，MP都是素数，但P＝11时，M11不是素数，因此M11不是梅森素。那么，什么是梅森素数呢？
python程序判断梅森素数_蓝桥杯每日一题（9）：梅森素数（python）
weixin_35712571的博客
02-04 572
Topic：假如一个数据的全部真因子之和相当于本身，则称它为“完全数”或“完美数”比如：6 = 1 + 2 + 328 = 1 + 2 + 4 + 7 + 14早在公元300很多年，欧几里得就得出了判断完全数的定律：若 2^n - 1 是素数，则 2^(n-1) * (2^n - 1) 是完全数。在其中 ^ 表明“乘方”计算，乘方的优先比四则运算高，比如：2^3 = 8， 2 * 2^3 = 16...
小学数学数学故事梅森素数：千年不休的探寻之旅2
09-09
超级计算机的使用极大地提高了梅森素数的搜索效率，但随着素数\(p\)的增加，寻找新的梅森素数变得越来越困难。全球的科学家和业余爱好者们持续竞争，致力于这一千年不休的探寻之旅，不断拓展人类对素数和数学知识的...
python求素数（代码+科普吹牛）
Mo_jian的博客
10-16 5875
在CSDN记录学习python的第一天：用python求素数。
第51个梅森质数（2的82589933-1）
04-23
从梅森质数的官网上下载下来的，当前最大的梅森质数，发现于2018年12月。因为没什么用，只是饱一瞬间的眼福，所以就免费了
梅森尼数
double_main的博客
12-20 7741
形如 2^n-1 的素数称为 梅森尼数（Mersenne Prime）例如 2²-1=3 , 2³-1=7 都是梅森尼数； 1722年，双目失明的瑞士数学大师欧拉证明了 2^31-1=2147483647 是一个素数，堪称当时世界上“已知最大素数”的一个记录； 试求出指数n<50的所有梅森尼数；1.说明：设置指数n循环，输入循环上限指数n（n>2），循环体中通过累乘t=t*2得t=2^n；根据梅森尼
反向数学归纳法的提出与周氏猜测的证明
zp235711的博客
04-13 9024
中国学者周海中根据已知的梅森素数及其排列，巧妙地运用联系观察法和不完全归纳法，于1992年2月正式提出了一个关于梅森素数分布的猜想，并首次给出其分布的精确表达式。 后来这一重要猜想被国际数学界命名为 “周氏猜测” 。 周氏猜测的基本内容为：当 22n&lt;p&lt;22n+12^{2^{n}}&lt;p&lt;2^{2^{n+1}}22n<p<22n...
余数定理问题和余数类问题的解法
wangychf的博客
03-31 1418
一、引言 Python里面有一个重要的求模运算符号“％”，作为一个小白，实验了好多次求模的运算，发现这个算法不同于一般的四则运算，其运算效率简直可以用神奇来形容。 例如以当今知道的最大质数——梅森素数为例，进行求模计算，速度快得惊人。当前知道的最大的梅森素数是第51个梅森素数，也是迄今为止知道的最大的素数。它的表示为： 2^82589933 – 1, 如果用十进制打开，这个数有24862048位，是2018年被证明为素数的。 在python中，如果直接计算这个数，一般的机器都是打不开的。如果做四则运算也是有
用Java模拟打字：深入解析 java.awt.Robot 的键盘控制艺术
码觉客的博客
04-28 1022
通过，我们可以实现强大的键盘自动化功能。对于简单的字符（英文字母、数字、基础标点等），可以通过模拟单个按键的按下和释放（可能需要配合 Shift 等修饰键）来实现，这需要建立字符到键码的映射并注意按键时序和延迟。对于复杂字符、中文或长文本，由于Robot不理解输入法逻辑，最可靠和常用的方法是将文本复制到系统剪贴板，然后模拟按下系统的粘贴快捷键。无论使用哪种方法，理解Robot的工作原理（模拟物理按键），处理好窗口焦点，并加入适当的延迟，是确保模拟输入成功的关键。虽然Robot。
Python学习笔记（三）（程序流程控制）
wsys_yysn的博客
04-24 1101
条件语句：通过实现分支逻辑。循环语句for遍历序列，while满足条件时循环。流程控制break终止循环，continue跳过当前迭代，pass占位。异常处理保证程序健壮性。掌握这些流程控制工具，可以编写更灵活、高效的 Python 程序！
Python项目--基于计算机视觉的手势识别控制系统
exlink2012的专栏
04-23 2616
随着人机交互技术的快速发展，传统的键盘、鼠标等输入设备已经不能满足人们对自然、直观交互的需求。手势识别作为一种非接触式的人机交互方式，具有操作自然、交互直观的特点，在智能家居、游戏控制、虚拟现实等领域有着广泛的应用前景。 本项目旨在开发一个基于计算机视觉的手势识别控制系统，通过摄像头捕获用户的手部动作，实时识别手势类型，并将识别结果转化为相应的控制命令，实现对计算机或其他设备的非接触式控制。
京东商品详情API数据爬取难度分析与解决方案
最新发布
Asher18870278351的博客
04-28 662
京东商品数据爬取是一项技术要求高、维护成本大的工程，需要综合运用网络爬虫、密码学分析和分布式系统等多领域知识。成功的爬虫系统需要在技术实现、资源投入和合规边界之间找到平衡点。随着电商平台安全技术的不断升级，爬取方也需要持续迭代技术手段，同时更应关注数据获取的合法合规性。
基于亚马逊云科技搭建企业问答系统
正在自我救赎的菜鸟。本人所有内容均不收费，可随意转发，复制
04-27 981
在当今信息密集的企业环境中，如何快速、安全地构建专属知识库成为提升效率的关键。本教程将手把手教你如何从零开始，借助 Amazon Bedrock 控制台与 DeepSeek 大语言模型，将企业内部文档转化为可交互的问答系统（RAG 架构）。无需任何编程经验，只需按照步骤操作，即可轻松完成搭建与体验。
实现准梅森素数改进的搜索方法
05-05
准梅森素数是指形如 $2^p-1$ 的素数，其中 $p$ 也是素数。现在有一种改进的搜索方法可以用来寻找更大的准梅森素数，具体步骤如下： 1. 选择一个大的质数 $q$，计算 $n=q+1$。 2. 用 $n$ 去试除所有小于 $\sqrt{n}$ 的素数，如果 $n$ 是素数，则继续。 3. 计算 $s=2^q-1$，如果 $s$ 不是素数，则返回第 1 步。 4. 用 $s$ 去试除所有小于 $\sqrt{s}$ 的素数，如果 $s$ 是素数，则找到了一个准梅森素数，返回 $s$，否则返回第 1 步。 这个搜索方法的改进之处在于，通过选择一个大的质数 $q$，可以让 $2^q-1$ 的大小更接近一个准梅森素数，从而减少试除的次数，提高效率。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值