离散化算法

原创于 2025-11-23 17:57:58 发布 · 683 阅读

9 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #c++ #数据结构

离散化算法

近期笔者在学习数据结构：哈希表时发现于离散化算法非常像，因此先总结离散化算法之后再总结哈希表

一、核心原理

1.问题背景

当处理的数据**取值范围非常大(>1e9)但实际出现的不重复数据量很少时(<=1e5)**时，直接使用数据作为数组下标会出现以下问题

空间浪费：数组要开1e9大小，超过内存限制（1e9个int 需要4GB,内存不足）
无法操作：内存无法分配，导致程序无法进行

2.核心思想

离散化是将大范围、但是稀疏的离散数据映射到小范围且连续的整数索引（如1,2,…m,m为不重复数据个数）的预处理技术。核心思想是压缩坐标，保留数据的相对大小和出现关系，丢弃无用的大范围间隔

3.核心步骤

离散化完整流程可以总结为4步：

收集数据：收集所有需要用到的关键数据（如插入的坐标，查询的区间边界等）
排序去重：对数据进行排序，删除其中的重复元素，得到唯一，有序的数据列表
建立映射：通过二分查找，将每个数据映射到对应的连续索引
处理任务：用映射后的索引替代原来的下标，进行后续操作。

二、代码实现与解析

以该例题区间和为例讲解代码
题目链接：https://www.acwing.com/problem/content/804/
题目描述

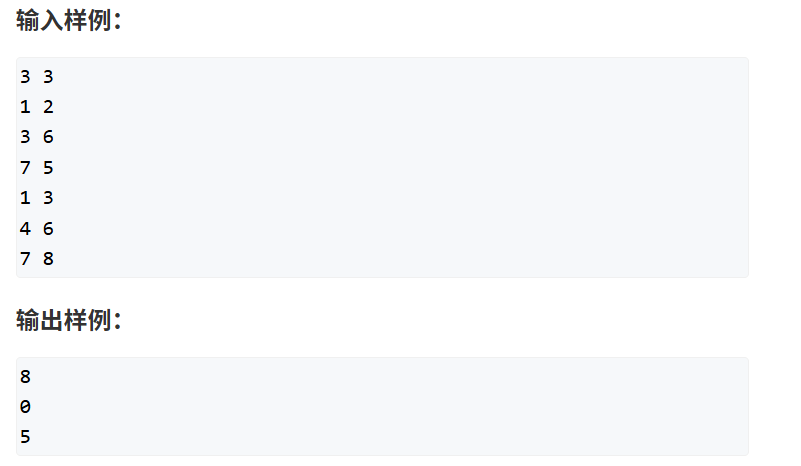
1. 初始数据结构定义

const int N = 3e5+10;  // 最大不重复关键字个数（3e5足够应对大部分场景）
typedef pair<int,int> PII;  // 存储插入操作（{x, c}）和查询操作（{l, r}）

int n, m;               // n：插入操作数；m：查询操作数
int a[N];               // 离散化后的数组（存储映射后的索引对应的累加值）
vector<PII> add, query;  // add：插入操作列表；query：查询操作列表
vector<int> alls;       // 存储所有需要离散化的关键字

2.收集关键字

收集所有会用到的坐标————插入的x、查询的l和r：

// 读入插入操作，收集x
for(int i = 0; i < n; i++) 
{
    int x, c;
    scanf("%d%d", &x, &c);
    alls.push_back(x);  // 收集插入坐标x
    add.push_back({x, c});  // 记录插入操作
}

// 读入查询操作，收集l和r
for(int i = 0; i < m; i++) 
{
    int l, r;
    scanf("%d%d", &l, &r);
    query.push_back({l, r});  // 记录查询操作
    alls.push_back(l);        // 收集查询左边界l
    alls.push_back(r);        // 收集查询右边界r
}

收集l和r的原因
查询的区间边界l和r可能不在插入的x中，但是需要通过离散化映射到索引，才能计算区间和

3.排序去重

对alls排序并删除重复元素得到唯一、有序的关键字列表：

sort(alls.begin(), alls.end());  // 排序：使关键字有序，为二分查找打基础
alls.erase(unique(alls.begin(), alls.end()), alls.end());  // 去重

unique(alls.begin(),alls.end()):将重复的元素移到数组末尾，返回不重复元素的尾部迭代器
erase():删除末尾的重复元素，使alls存储所有不重复的关键字（有序）

4.建立映射（find函数）

通过二分查找，将关键字x映射到连续索引（下标从1开始）

int find(int x) 
{
    int l = 0, r = alls.size() - 1;
    while(l < r) 
    {
        int mid = l + r >> 1;  // 等价于 (l+r)/2，避免溢出
        if(alls[mid] >= x) r = mid;  // 找第一个 >= x 的位置
        else l = mid + 1;
    }
    return l + 1;  // 映射为1-based索引（a[0]留作前缀和的哨兵）
}

二分时间复杂度：O(logm)（m为不重复关键字个数，m<=3e5,因此logm约等于19效率极高）
下标从1开始的优势：前缀和计算时s[r]-s[l-1] 直接对应区间[l,r]的和，无需考虑l = 0的边界问题

5.处理任务（插入+查询）

用映射后的索引替代原关键字，进行插入和区间查询工作：

插入：累加值到映射后的索引：

for(int i = 0; i < add.size(); i++) 
{
    int x = add[i].first;    // 原插入坐标
    int c = add[i].second;   // 累加值
    int k = find(x);         // 映射为1-based索引
    a[k] += c;               // 在映射后的索引位置累加c
}

前缀和预处理

for(int i = 1; i <= alls.size(); i++)
{
    a[i] += a[i-1];  // 前缀和数组：a[i] 表示前i个索引的累加和
}

前缀和时间复杂度：O(m)(m为不重复关键字个数)

查询区间和

for(int i = 0; i < query.size(); i++) 
{
    int l = query[i].first;  // 原查询左边界
    int r = query[i].second; // 原查询右边界
    // 映射为1-based索引，计算区间和：a[r映射] - a[l映射-1]
    int k1 = find(l);
    int k2 = find(r);
    printf("%d\n", a[k2] - a[k1-1]);
}

三、关键要点

映射唯一：排序去重使得每个关键字对应唯一索引，使得映射无歧义
下标从1开始，方便前缀和计算，避免l = 0时a[l-1]越界
关键字完整性：必须收集所有可能用到的坐标（包括插入的x和查询的l和r），否则映射会缺失导致查询错误
时间复杂度：
- 收集关键字：O(n+m)
- 排序去重：O(mlogm),(m为关键字总数)
- 插入+查询：O((n+m)logm)
  整体复杂度为O((n+m)logm)