离散数学速成

孤独一里

已于 2024-06-20 17:20:45 修改

阅读量642

点赞数 4

文章标签：数据结构 c语言

于 2024-06-17 20:41:37 首次发布

本文链接：https://blog.csdn.net/2401_83524644/article/details/139753716

版权

1.真值表法

二进制	P	Q	R	~Q	P V~Q	R->Q	(P V~Q)->(R->Q)
0	0	0	0	1	1	1	1
1	0	0	1	1	1	0	0
2	0	1	0	0	0	1	1
3	1	0	0	1	1	1	1
4	0	1	1	0	0	1	1
5	1	0	1	1	1	0	0
6	1	1	0	0	1	1	1
7	1	1	1	0	1	1	1

所以 m000 | m010 | m011 | m110 | m111 真赋值

M001 & M101 假赋值

2.使用真值表法解主析取泛式主合取范式

(P |~Q)->(R->Q)

~(P |~Q) | (~R | Q)蕴含等值式

//(~P & Q) | (~R & Q)德摩根定律

主析取泛式：（~P & ~Q & ~R) |（~P & Q & ~R) |（~P & Q & R) | （P & Q & ~R) |

（P & Q & R)

主合取范式：（P | Q | R) |（~P | Q | ~R)

3.2的正解

（P | Q) ^ (P->R)

=（P | Q) ^ (~P | R) 蕴含等值式

=（~P ^ Q ^ ~R) |（~P ^ Q ^ R) | （P ^ ~Q ^ R) |（P ^ Q ^ R)

= m010 | m011 | m101 v m111

= M2 | M3 | M5 | M7

= M000 & M001 & M100 & M110

= M0 & M1 & M4 & M6

= （P | Q | R) &（P | Q | ~R) &（~P | Q | R) &（~P | ~Q | R)

4.推理定律

附加定律 : A=>(A | B)

化简率：（A & B) => A

假言推理：（A ->B) & A => B

拒取式：（A->B)&~B =>~A

析取三段论：（A | B）& ~B => A

5.CP规则

解：1.P & S 附加前提

2.P->(Q&R)

3.P 1.化简律

4.（Q&R）假言推理

5.S 1.化简律

6.S->~Q

7.~Q 5.6.假言推理

8.R 4.7析取三段论

9.（P&S）->R cp规则

6.前束范式

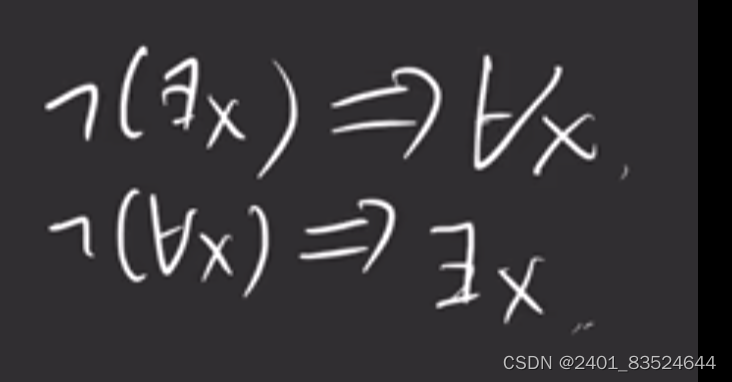
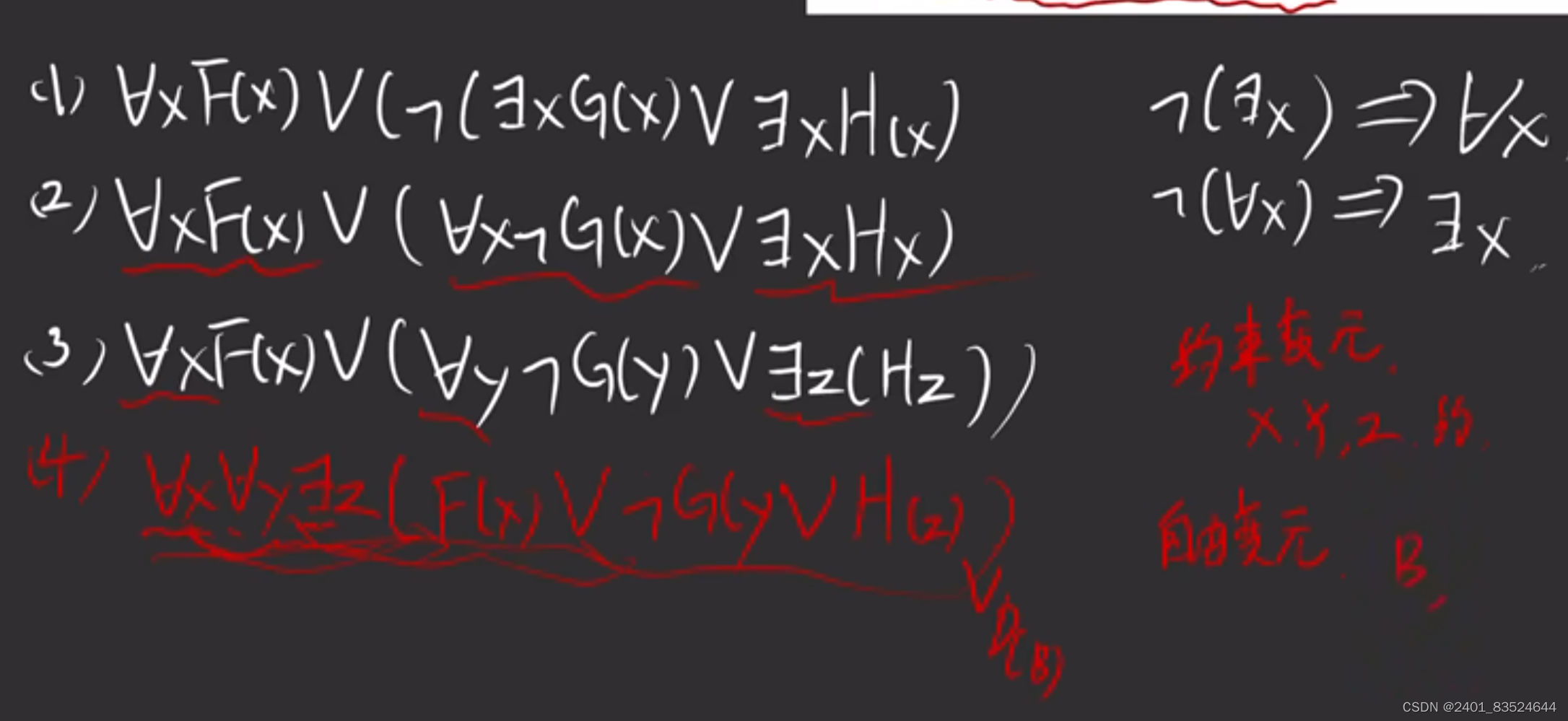
7.自反，反自反，自反闭包

R1={<a,a> , <b,b> , <c,c>}为自反

闭包实际上指的是一种过程，就是这个集合缺什么元素就能达到某种性质，你把缺的元素补上这个过程就叫闭包

R2={<a,a> , <b,b> ,}

比如这里的自反闭包，你将缺的{c，c}补上后这个集合就有了完整的自反性，那么你就完成了自反闭包。

R2={<a,a> , <b,b> , <c,c>}自反闭包

R3={<a,b> , <b,a>}为反自反

8.对称，反对称，对称闭包

R3={<a,b> , <a,c>}反对称

R3={<a,b> , <a,c> ,<b,a> , <c,a>}对称闭包

9.传递，非传递，传递闭包

R1={<a,b> ,<b,c> ,<c,b>}

传递就是任意两对间第一对的最右边是否与第二对的最左边相同

如果相同便删除这两个组成新的一对，判断此对是否再式子中存在

若是全部存在便是传递

例如：<a,b> ,<b,c> -><a,c>

<b,c> ,<c,b>-><b,b>

<c,b>,<b,c> -><c,c>

<a,b> ,<c,b>没有 <b,c> <a,b> 没有 <c,b>,<a,b>没有

而在R1中<c,c>，<b,b>，<a,c>并不存在，所以R1为非传递

将这三个补完便是传递闭包

10.关系矩阵

11.复合运算

12.命题等含义具体解释

命题是一个可以判断真假的陈述句。
可满足式： 一个公式，如果至少存在一组真值指派使其为真，则该公式是可满足式。
永真式： 一个公式，如果对于所有真值指派，它都为真，则该公式是永真式。
永假式： 一个公式，如果对于所有真值指派，它都为假，则该公式是永假式。
主析取范式 (DNF)： 一个布尔表达式表示为多个文字的析取 (OR) 的形式，每个析取项包含所有变量，且每个变量只出现一次。
主合取范式 (CNF): 几个合取项的合取 (AND)，每个合取项包含所有变量，且每个变量只出现一次。例如： (x+¬y)(¬x+¬y)。
极小项： 一个包含所有变量且每个变量都取定真值或假值的析取项。

13.基本等值式

14.哈塞图

上界 (Upper Bound)

一个元素的上界是指，在这个偏序关系中，比它 大或等于 它的所有元素。
更准确地说，对于一个集合 S 中的元素 x，如果存在一个元素 y 使得 x ≤ y，那么 y 就是 x 的上界。
在哈斯图中，上界通常位于元素的上方。

下界 (Lower Bound)

一个元素的下界是指，在这个偏序关系中，比它 小或等于 它的所有元素。
更准确地说，对于一个集合 S 中的元素 x，如果存在一个元素 y 使得 y ≤ x，那么 y 就是 x 的下界。
在哈斯图中，下界通常位于元素的下方。

最小上界 (Least Upper Bound, LUB)

最小上界是指所有上界中 最小的那个。
在哈斯图中，最小上界通常是元素的上界中 离它最近的 元素。

最大下界 (Greatest Lower Bound, GLB)

最大下界是指所有下界中 最大的那个。
在哈斯图中，最大下界通常是元素的下界中 离它最近的 元素。

15.图的基本概念

1. 基本概念

1.1 图的定义

图（Graph）：图 GGG 由一对集合 VVV 和 EEE 组成，记作 G=(V,E)G=(V, E)G=(V,E)，其中 VVV 是顶点的集合，EEE 是边的集合。每条边是两个顶点的无序对。

1.2 特殊类型的图

简单图（Simple Graph）：没有重边（同一对顶点之间有多条边）和自环（顶点连接到自身）的图。
多重图（Multigraph）：允许重边的图。
伪图（Pseudograph）：允许自环和重边的图。
无向图（Undirected Graph）：边是无序对的图。
有向图（Directed Graph, Digraph）：边是有序对的图，边有方向。
加权图（Weighted Graph）：每条边有一个权重的图。
子图（Subgraph）：图 GGG 的子图是一个由 GGG 的部分顶点和部分边构成的图。

1.3 顶点和边的术语

度（Degree）：顶点的度是连接该顶点的边的数量。无向图中顶点的度记作 deg(v)deg(v)deg(v)。
入度（In-Degree）：有向图中指向该顶点的边的数量，记作 deg−(v)deg^-(v)deg−(v)。
出度（Out-Degree）：有向图中从该顶点出发的边的数量，记作 deg+(v)deg^+(v)deg+(v)。

1.4 握手定律

在一个无向图中，所有顶点的度数之和等于边数的两倍。

2. 路径与圈

2.1 路径

路径（Path）：一系列顶点的序列，其中每两个连续顶点之间都有边连接。
简单路径（Simple Path）：路径中没有重复顶点。
闭路径（Closed Path）：路径的起点和终点是同一个顶点。

2.2 圈

圈（Cycle）：至少有一条边的闭路径，并且除了起点和终点外，路径中的所有顶点都不同。
哈密顿圈（Hamiltonian Cycle）：访问图中每个顶点恰好一次的圈。
欧拉圈（Eulerian Cycle）：访问图中每条边恰好一次的圈。

3. 连通性

3.1 无向图的连通性

连通图（Connected Graph）：无向图中任意两个顶点之间都存在路径。
连通分量（Connected Component）：极大连通子图。

3.2 有向图的连通性

强连通图（Strongly Connected Graph）：有向图中任意两个顶点 uuu 和 vvv 之间都存在从 uuu 到 vvv 以及从 vvv 到 uuu 的路径。
弱连通图（Weakly Connected Graph）：将所有有向边看作无向边后，图是连通的。

3.3 回路

1. 简单回路 (Simple Cycle)

简单回路是指在回路中，所有顶点 只出现一次，除了起点和终点 (它们相同)。换句话说，简单回路不能包含重复的顶点 (除了起点和终点)。

2. 复杂回路 (Complex Cycle)

复杂回路是指在回路中，至少存在一个顶点 出现两次或更多次。

点割集和边割集是图论中用来描述图的连通性、可分割性的概念。

3.4 割集

点割集 (Vertex Cut)

点割集是指图中一个顶点集合，移除这些顶点以及与它们相连的边，会导致图中 至少两个连通分量 出现。
换句话说，点割集是一个能够将图分割成多个连通部分的最小顶点集合。

边割集 (Edge Cut)

边割集是指图中一个边集合，移除这些边会导致图中 至少两个连通分量 出现。
换句话说，边割集是一个能够将图分割成多个连通部分的最小边集合。

举例说明：

假设有一个图 G，如图所示：

       A
      / \
     /   \
    B --- C
     \   /
      \ /
       D

点割集:
- {B, C} 是一个点割集，移除它们后，图将被分割成两个连通分量：{A} 和 {D}。
- {A, D} 也是一个点割集。
边割集:
- {(A, B), (A, C)} 是一个边割集，移除它们后，图将被分割成两个连通分量：{A} 和 {B, C, D}。
- {(B, D), (C, D)} 也是一个边割集。

4. 树与生成树

4.1 树

树（Tree）：一种特殊的连通无环无向图。树中任意两个顶点之间有且只有一条路径。
根树（Rooted Tree）：指定一个顶点为根的树。

4.2 生成树

生成树（Spanning Tree）：连通图的生成树是包含该图所有顶点的极小连通子图。
最小生成树（Minimum Spanning Tree, MST）：加权图中所有生成树中权重之和最小的生成树。

5. 图的算法

5.1 深度优先搜索 (DFS)

深度优先搜索是一种图的遍历方法，采用递归方式从一个顶点开始尽可能深入地访问未访问的顶点。

void DFS(int v, vector<bool> &visited, const vector<vector<int>> &adjList) {
    visited[v] = true;
    cout << v << " ";
    for (int u : adjList[v]) {
        if (!visited[u]) {
            DFS(u, visited, adjList);
        }
    }
}

5.2 广度优先搜索 (BFS)

广度优先搜索是一种图的遍历方法，采用队列从一个顶点开始逐层访问所有顶点。

void BFS(int start, const vector<vector<int>> &adjList) {
    vector<bool> visited(adjList.size(), false);
    queue<int> q;
    q.push(start);
    visited[start] = true;
    
    while (!q.empty()) {
        int v = q.front();
        q.pop();
        cout << v << " ";
        
        for (int u : adjList[v]) {
            if (!visited[u]) {
                q.push(u);
                visited[u] = true;
            }
        }
    }
}

5.3 最短路径算法

Dijkstra算法：用于带权图，求从单个源顶点到其他顶点的最短路径。
Floyd-Warshall算法：用于带权图，求任意两顶点之间的最短路径。

5.4 最小生成树 (Minimum Spanning Tree)

Kruskal算法：使用边的贪心策略，选择不形成环的最小边构造最小生成树。
Prim算法：使用顶点的贪心策略，从一个顶点开始逐步扩展生成树。

6.其他图

6.1欧拉图

定义: 一个无向图被称为欧拉图，如果存在一条路径 (欧拉回路)，能够遍历图中所有边恰好一次，并且最后回到起点。
判定条件: 欧拉图必须满足以下两个条件：
- 连通性: 图必须是连通的，即任何两个顶点之间都存在路径。
- 偶数度: 图中所有顶点的度数必须都是偶数。
应用: 欧拉图在实际应用中有很多例子，例如：
- 旅行推销员问题: 寻找一条最短路径，经过所有城市一次。
- 网络路由: 设计一个网络路径，以便所有节点都能访问所有其他节点。
- 地图绘制: 寻找一条路径，可以绘制所有街道一次。

欧拉通路是简单通路，欧拉回路是简单回路

环不影响图的欧拉性

7.集合

1. 集合的定义

集合是一个包含一组不重复元素的集体。元素可以是任何类型的对象，例如数字、字母、对象等。

2. 集合的表示

集合通常用大写字母表示，元素用小写字母表示，元素之间用逗号分隔，并用花括号括起来。例如：

A={1,2,3,4}
B={a,b,c}

集合的元素可以是有限的，也可以是无限的。例如，自然数的集合 N={1,2,3,…}

3. 集合的类型

有限集：包含有限个元素的集合，例如{1,2,3}。
无限集：包含无限个元素的集合，例如自然数集 N。
空集：不包含任何元素的集合，记作 ∅或 {}。
子集：如果集合 A 的所有元素也是集合 B 的元素，则 A 是 B 的子集，记作 A⊆B
幂集：一个集合的所有子集的集合，记作 P(A)。

4. 基本操作

并集 (Union)：集合 A 和集合 B的并集包含在 A 或 B 中的所有元素，记作 A∪B
- 例如，{1,2}∪{2,3}={1,2,3}
交集 (Intersection)：集合 A和集合 B 的交集包含在 A 和 B 中都存在的元素，记作 A∩B。
- 例如，{1,2}∩{2,3}={2}
差集 (Difference)：集合 A 的差集包含在 A 中但不在 B 中的元素，记作 A−B 或 A∖B。
- 例如，{1,2}−{2,3}={1}
补集 (Complement)：在全集 U 中，集合 A 的补集包含不在 A 中的元素，记作 A′ 或。
- 例如，如果 U={1,2,3,4}且 A={1,2}则 A′={3,4}