汉字笔顺动画技术剖析

this.segments = [path[(index[1] + n - 1) % n], path[index[1]]];
this.point = this.segments[0].end;
assert(Point.valid(this.point), this.apoint);
assert(Point.equal(this.point, this.segments[1].start), path);
this.tangents = [
Point.subtract(this.segments[0].end, this.segments[0].start),
Point.subtract(this.segments[1].end, this.segments[1].start),
];
const threshold = Math.pow(MIN_CORNER_TANGENT_DISTANCE, 2);
if (this.segments[0].control !== undefined &&
Point.distance2(this.point, this.segments[0].control) > threshold) {
this.tangents[0] = Point.subtract(this.point, this.segments[0].control);
}
if (this.segments[1].control !== undefined &&
Point.distance2(this.point, this.segments[1].control) > threshold) {
this.tangents[1] = Point.subtract(this.segments[1].control, this.point);
}
this.angles = this.tangents.map(Point.angle);
const diff = Angle.subtract(this.angles[1], this.angles[0]);
this.corner = diff < -MIN_CORNER_ANGLE;
return this;
}

2.3 Corner Match Scoring 通过NN评分Corner匹配度

检测出一组corner数据后，就要对这些corner进行一对一匹配，但在匹配前还需要评判哪些corner更有可能连接起来。开源库采用神经网络算法计算corner间的匹配度，它将成为匹配算法中的权重值，使匹配结果更贴近现实情况。

const scoreCorners = (ins, out, classifier) => {
return classifier(getFeatures(ins, out));
}

import {NEURAL_NET_TRAINED_FOR_STROKE_EXTRACTION} from ‘/lib/net’;
import {stroke_extractor} from ‘/lib/stroke_extractor’;

Meteor.startup(() => {
const input = new convnetjs.Vol(1, 1, 8 /* feature vector dimensions */);
const net = new convnetjs.Net();
net.fromJSON(NEURAL_NET_TRAINED_FOR_STROKE_EXTRACTION);
const weight = 0.8;

const trainedClassifier = (features) => {
input.w = features;
const softmax = net.forward(input).w;
return softmax[1] - softmax[0];
}

stroke_extractor.combinedClassifier = (features) => {
return stroke_extractor.handTunedClassifier(features) +
weight*trainedClassifier(features);
}
});

2.4 Corner Matching 通过匈牙利算法进行Corner匹配

在2.3小节中已经通过神经网络产生了权重，接下来就可以使用最简单的匈牙利算法，实现corner匹配。

const matchCorners = (corners, classifier) => {
const matrix = [];
for (let i = 0; i < corners.length; i++) {
matrix.push([]);
for (let j = 0; j < corners.length; j++) {
matrix[i].push(scoreCorners(corners[i], corners[j], classifier)); //corner之间相关性
}
}
for (let i = 0; i < corners.length; i++) {
for (let j = 0; j < corners.length; j++) {
const reversed_score = matrix[j][i] - REVERSAL_PENALTY;
if (reversed_score > matrix[i][j]) {
matrix[i][j] = reversed_score;
}
}
}
return (new Hungarian(matrix)).x_match;
}

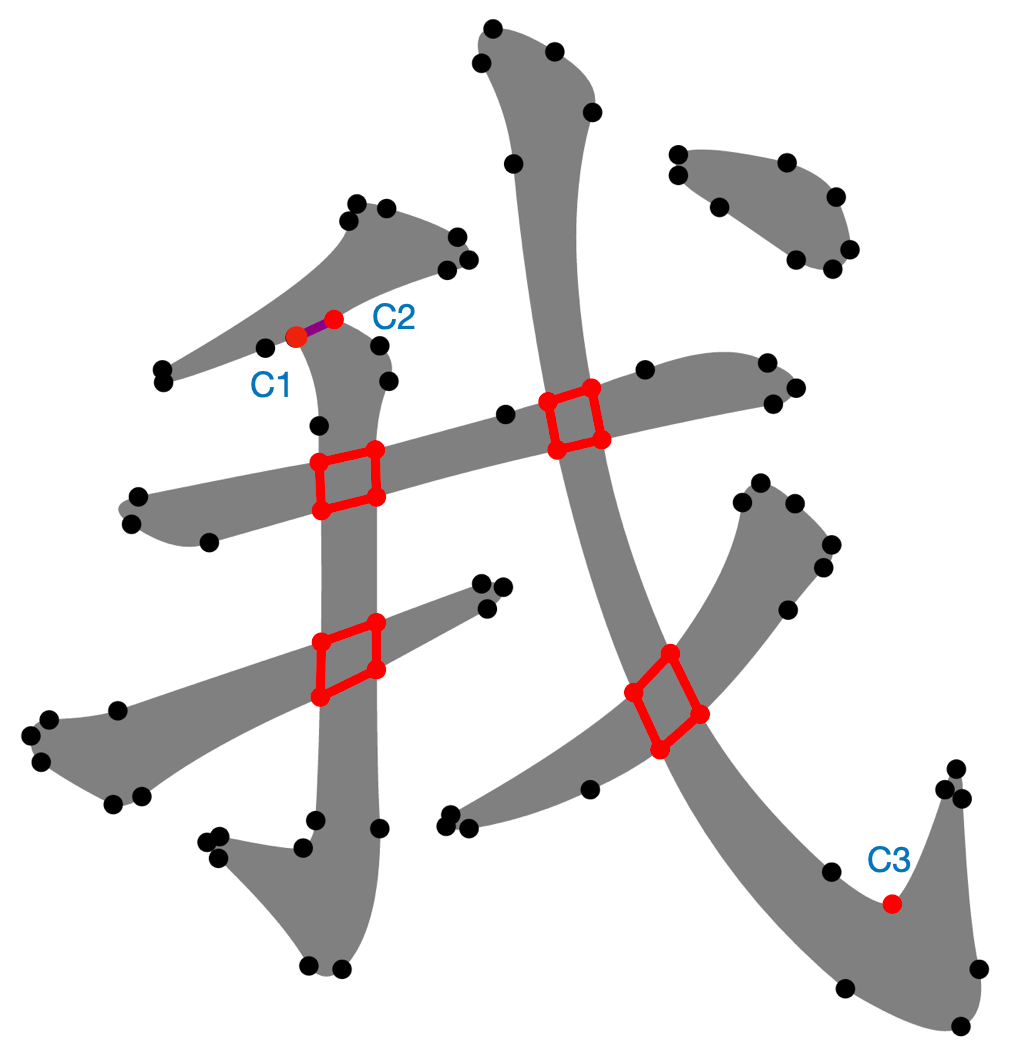
2.5 Make Bridges 连通配对端点拆分笔画

依据2.4小节的匹配结果返回一组bridge，其中每个bridge包含两个corner。跟踪轮廓的同时连通corner，就可以提取出每个笔画的轮廓数据，实现笔画拆分。值得注意的是，当遇到多个bridge时，选择与当前path构成最大角度的bridge。

const getBridges = (endpoints, classifier) => {
const result = [];
const corners = endpoints.filter((x) => x.corner);
const matching = matchCorners(corners, classifier);
for (let i = 0; i < corners.length; i++) {
const j = matching[i];
if (j <= i && matching[j] === i) {
continue;
}
result.push([Point.clone(corners[i].point), Point.clone(corners[j].point)]);
}
result.map(checkBridge);
return result;
}

const stroke_paths = extractStrokes(paths, endpoints, bridges, log);
const strokes = stroke_paths.map((x) => svg.convertPathsToSVGPath([x]));

3. Medians 笔画中点生成

在第二节中实现了笔画的拆分，得到每个笔画的轮廓数据。依据轮廓数据可以进一步生成笔画的中点骨架。轮廓决定单个笔画的绘制范围，而中点则决定了绘制的顺序和方向。结合轮廓和中点数据，就可以实现单个笔画的绘制动画。接下来就让我们一起了解，如何通过轮廓数据生成中点。

3.1 Polygon Approximation 端点加密

首先，为了提高中点生成结果的可靠性，需要先采用矢量图形的多边形近似方法进行轮廓点加密。TrueType字体利用二次贝赛尔曲线和直线来描述字形的轮廓，因此加密公式如下：

svg.getPolygonApproximation = (path, approximation_error) => {
const result = [];
approximation_error = approximation_error || 64;
for (let x of path) {
const control = x.control || Point.midpoint(x.start, x.end);
const distance = Math.sqrt(Point.distance2(x.start, x.end));
const num_points = Math.floor(distance/approximation_error);
for (let i = 0; i < num_points; i++) {
const t = (i + 1)/(num_points + 1);
const s = 1 - t;
result.push([ssx.start[0] + 2stcontrol[0] + ttx.end[0],
ssx.start[1] + 2stcontrol[1] + ttx.end[1]]);
}
result.push(x.end);
}
return result;
}

3.2 Polygon Voronoi 通过冯洛诺伊图（泰森多边形）生成中点

得到加密的轮廓点数据后，就可以通过泰森多边形生成中点。那什么是泰森多边形呢？

首先对一组零散控制点做如下操作：

1. 将三个相邻控制点连成一个三角形
2. 对三角形的每条边做垂直平分线
3. 这些垂直平分线会组成连续多边形

这些连续多边形就是泰森多边形，又叫冯洛诺伊图（Voronoi diagram），得名于Georgy Voronoi。在IS和地理分析中经常采用泰森多边形进行快速插值，分析地理实体的影响区域，是解决邻接度问题的又一常用工具。

通过原理可以了解到，泰森多边形每个顶点是对应三角形的外接圆圆心，因此它到这些控制点的距离相等。

var sites = [{x:300,y:300}, {x:100,y:100}, {x:200,y:500}, {x:250,y:450}, {x:600,y:150}];
// xl, xr means x left, x right
// yt, yb means y top, y bottom
var bbox = {xl:0, xr:800, yt:0, yb:600};
var voronoi = new Voronoi();
// pass an object which exhibits xl, xr, yt, yb properties. The bounding
// box will be used to connect unbound edges, and to close open cells
result = voronoi.compute(sites, bbox);
// render, further analyze, etc.

按照这个思路，可以将笔画的轮廓点作为控制点，生成泰森多边形。提取泰森多边形的顶点作为笔画中心点。

const findStrokeMedian = (stroke) => {
…
for (let approximation of [16, 64]) {
polygon = svg.getPolygonApproximation(paths[0], approximation);
voronoi = voronoi || new Voronoi;
const sites = polygon.map((point) => ({x: point[0], y: point[1]}));
const bounding_box = {xl: -size, xr: size, yt: -size, yb: size};
try {
diagram = voronoi.compute(sites, bounding_box);
break;
} catch(error) {
console.error(WARNING: Voronoi computation failed at ${approximation}.);
}
}
…
}

最后

下面是有几位Android行业大佬对应上方技术点整理的一些进阶资料。希望能够帮助到大家提升技术

高级UI，自定义View

UI这块知识是现今使用者最多的。当年火爆一时的Android入门培训，学会这小块知识就能随便找到不错的工作了。

不过很显然现在远远不够了，拒绝无休止的CV,亲自去项目实战，读源码，研究原理吧！

《Android学习笔记总结+移动架构视频+大厂面试真题+项目实战源码》，点击传送门，即可获取！
入门培训，学会这小块知识就能随便找到不错的工作了。

不过很显然现在远远不够了，拒绝无休止的CV,亲自去项目实战，读源码，研究原理吧！

[外链图片转存中…(img-G0KGnC1E-1715104073593)]

《Android学习笔记总结+移动架构视频+大厂面试真题+项目实战源码》，点击传送门，即可获取！