一文速学数模-时序预测模型(一)灰色预测一文详解+Python实例代码_灰色关联度时序预测(1)

最新推荐文章于 2024-05-02 01:13:24 发布

2401_84166005

最新推荐文章于 2024-05-02 01:13:24 发布

阅读量791

点赞数 24

分类专栏： 2024年程序员学习文章标签： python 开发语言

本文链接：https://blog.csdn.net/2401_84166005/article/details/137893547

版权

2024年程序员学习专栏收录该内容

85 篇文章 0 订阅

订阅专栏

先自我介绍一下，小编浙江大学毕业，去过华为、字节跳动等大厂，目前阿里P7

深知大多数程序员，想要提升技能，往往是自己摸索成长，但自己不成体系的自学效果低效又漫长，而且极易碰到天花板技术停滞不前！

因此收集整理了一份《2024年最新大数据全套学习资料》，初衷也很简单，就是希望能够帮助到想自学提升又不知道该从何学起的朋友。

既有适合小白学习的零基础资料，也有适合3年以上经验的小伙伴深入学习提升的进阶课程，涵盖了95%以上大数据知识点，真正体系化！

由于文件比较多，这里只是将部分目录截图出来，全套包含大厂面经、学习笔记、源码讲义、实战项目、大纲路线、讲解视频，并且后续会持续更新

如果你需要这些资料，可以添加V获取：vip204888 （备注大数据）

正文

3.系数求解

接下来就到了最关键的一部，想要求解上述微分方程：

$\frac{dx{(1)}}{dt}+ax{(1)}(t)=b$

就必须解出系数a和b，让微分方程的解与真实的已知数据最接近。函数表达式的参数a和u未知，而变量t和x^(1)的数值已知，这种问题就要用最小二乘法，通过最小化误差的平方和求得最佳的参数a和b。

1、数据是离散的而不是连续的，所以：

$\frac{dx^{(1)}}{dt}$ 写作 $\frac{\Delta x^{(1)}}{\Delta t}$

2.根据累加生成序列公式可知：

$\Delta x{(1)}=x{(1)}(t)-x{(1)}(t-1)=x{(0)}(t)$

3.由1和2可得到

$x{(0)}(t)+ax{(1)}(t)=d$

4.移项得：

$x{(0)}(t)=-ax{(1)}(t)+d$

5、式子左边是已知数据，右边就是含有未知数的函数，此时就可用最小二乘法求出参数a和u

对于最小二乘法的求解在我的一篇文章有详细描述：

一文速学-最小二乘法曲线拟合算法详解+项目代码

这里就不再展开描述求解过程，仅对于计算后的结果构成：

数据矩阵 $B$ ：

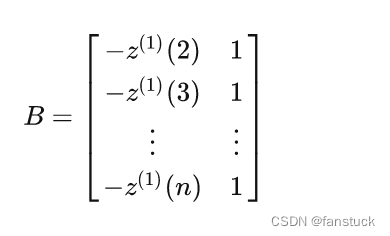
数据向量 $Y$ ：

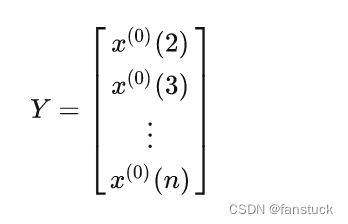
其中 $z^{(1)}$ 为加权平均值：

计算系数 $\hat{u}$ (最小二乘法)：

对前面的微分方程求解可得：

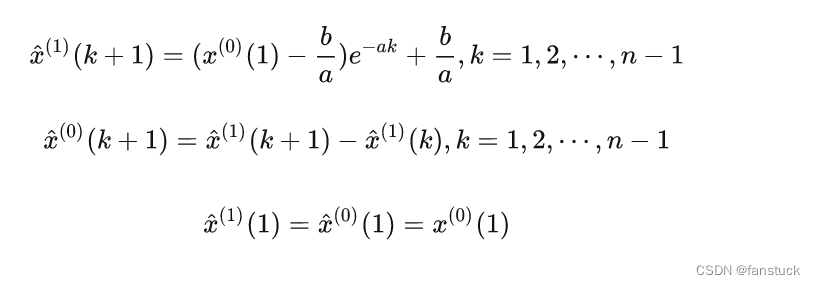
由上面三式可得：(最终结果)

4.残差检验与级比偏差检验

残差检验 $\varepsilon (k)$ :

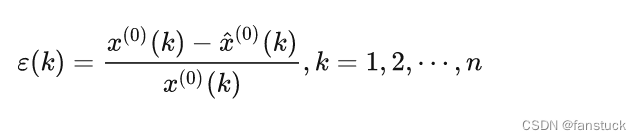
如果 $\varepsilon (k)$ <0.2,，则可认为达到一般要求；如果 $\varepsilon (k)$ <0.1，则认为达到较高的要求。

级比偏差检验 $\rho (k)$ :

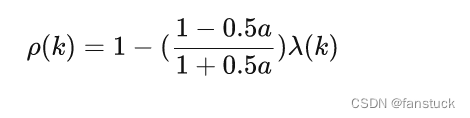
如果 $\rho (k)<0.2$ ，则可认为达到一般要求；如果 $\rho (k)<0.2$ ，则认为达到较高的要求。

四、Python实例实现

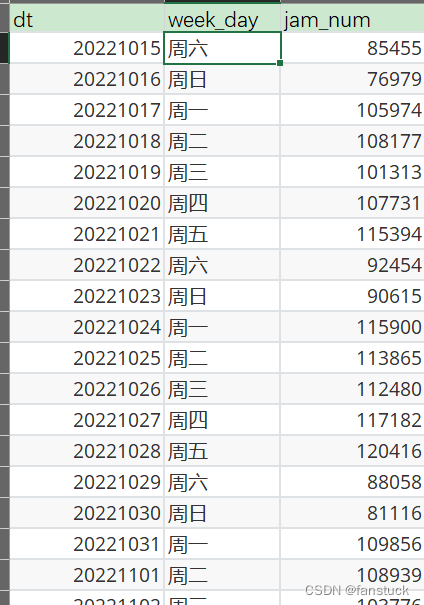
我们通过得到的周数拥堵车辆数据进行测试：

import numpy as np
import pandas as pd
from decimal import *
import matplotlib.pyplot as plt
def Grade_ratio_test(X0):
    lambds = [X0[i - 1] / X0[i] for i in range(1, len(X0))]
    X_min = np.e ** (-2 / (len(X0) + 1))
    X_max = np.e ** (2 / (len(X0) + 1))
    for lambd in lambds:
        if lambd < X_min or lambd > X_max:
            print('该数据未通过级比检验')
            return False
    print('该数据通过级比检验')
    return True
def model_train(X0_train):
    #AGO生成序列X1
    X1 = X0_train.cumsum()
    Z= (np.array([-0.5 * (X1[k - 1] + X1[k]) for k in range(1, len(X1))])).reshape(len(X1) - 1, 1)
    # 数据矩阵A、B
    A = (X0_train[1:]).reshape(len(Z), 1)
    B = np.hstack((Z, np.ones(len(Z)).reshape(len(Z), 1)))
    # 求灰参数
    a, u = np.linalg.inv(np.matmul(B.T, B)).dot(B.T).dot(A)
    u = Decimal(u[0])
    a = Decimal(a[0])
    print("灰参数a：", a, "，灰参数u：", u)
    return u,a
def model_predict(u,a,k,X0):
    predict_function =lambda k: (Decimal(X0[0]) - u / a) * np.exp(-a * k) + u / a 
    X1_hat = [float(predict_function(k)) for k in range(k)]
    X0_hat = np.diff(X1_hat)
    X0_hat = np.hstack((X1_hat[0], X0_hat))
    return X0_hat
'''
根据后验差比及小误差概率判断预测结果
:param X0_hat: 预测结果
:return:
'''
def result_evaluate(X0_hat,X0):
    S1 = np.std(X0, ddof=1)  # 原始数据样本标准差
    S2 = np.std(X0 - X0_hat, ddof=1)  # 残差数据样本标准差
    C = S2 / S1  # 后验差比
    Pe = np.mean(X0 - X0_hat)
    temp = np.abs((X0 - X0_hat - Pe)) < 0.6745 * S1    
    p = np.count_nonzero(temp) / len(X0)  # 计算小误差概率
    print("原数据样本标准差：", S1)
    print("残差样本标准差：", S2)
    print("后验差比：", C)
    print("小误差概率p：", p)
if __name__ == '__main__':
    plt.rcParams['font.sans-serif'] = ['SimHei']  # 步骤一（替换sans-serif字体）
    plt.rcParams['axes.unicode_minus'] = False  # 步骤二（解决坐标轴负数的负号显示问题）
        # 原始数据X
    
    data = pd.read_excel('./siwei_day_traffic.xlsx')
    X=data[data['week_day']=='周五'].jam_num[:5].astype(float).values
    print(X)
    # 训练集
    X_train = X[:int(len(X) * 0.7)]
    # 测试集
    X_test = X[int(len(X) * 0.7):]
 
    Grade_ratio_test(X_train)  # 判断模型可行性
    a,u=model_train(X_train)  # 训练
    Y_pred = model_predict(a,u,len(X),X)  # 预测
    Y_train_pred = Y_pred[:len(X_train)]
    Y_test_pred = Y_pred[len(X_train):]
    score_test = result_evaluate(Y_test_pred, X_test)  # 评估
 
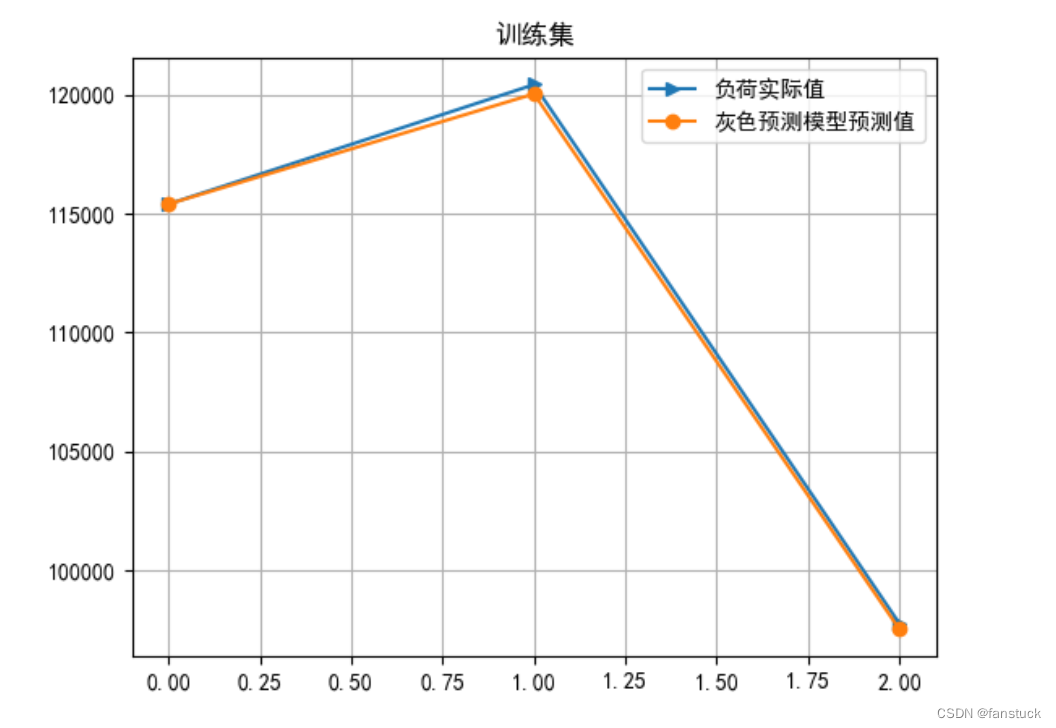
    # 可视化
    plt.grid()
    plt.plot(np.arange(len(X_train)), X_train, '->')
    plt.plot(np.arange(len(X_train)), Y_train_pred, '-o')
    plt.legend(['负荷实际值', '灰色预测模型预测值'])
    plt.title('训练集')
    plt.show()
 
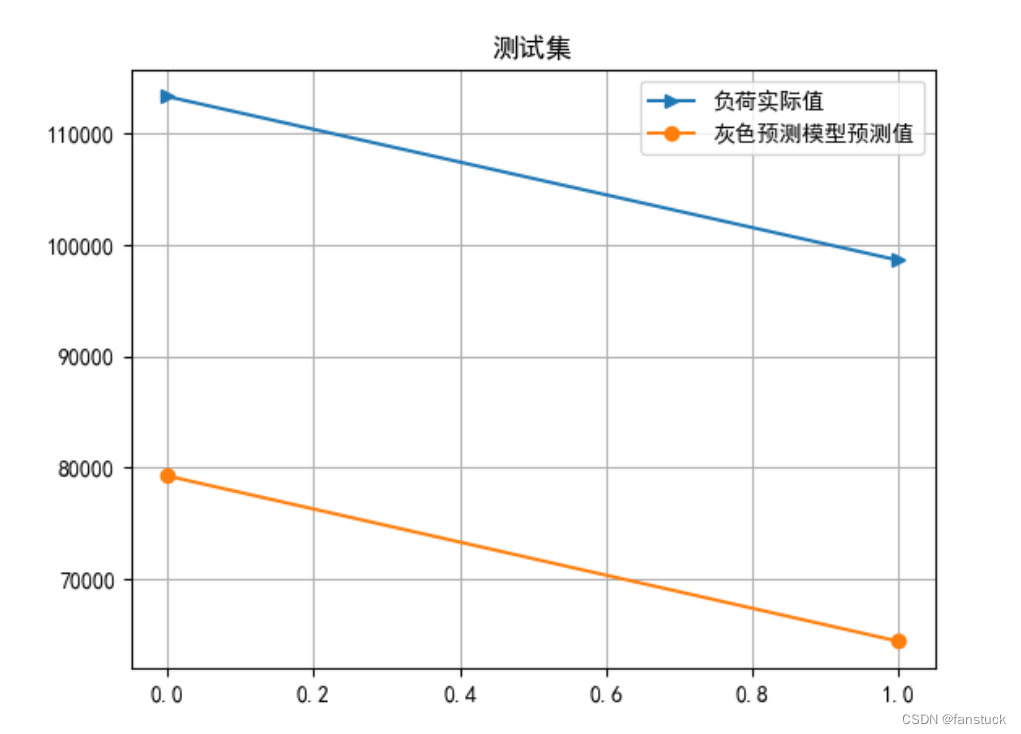
    plt.grid()
    plt.plot(np.arange(len(X_test)), X_test, '->')
    plt.plot(np.arange(len(X_test)), Y_test_pred, '-o')
    plt.legend(['负荷实际值', '灰色预测模型预测值'])
    plt.title('测试集')
    plt.show()

[115394. 120416.  97759. 113309.  98603.]
rho: [1.0435204603358927, 0.41456681226411096]
rho_ratio: [0.3972771287404067]
数据通过光滑校验
该数据通过级比检验
灰参数a： 0.20769565715594995314319248791434802114963531494140625 ，灰参数u： 156887.7727878994191996753215789794921875
原数据样本标准差： 10398.712324129368
残差样本标准差： 107.91252463173271
后验差比： 0.01037748918020652
小误差概率p： 1.0

总结

模型优点：数据少且无明显规律时可用，利用微分方程挖掘数据本质规律。

模型缺点：灰色预测只适合短期预测、指数增长的预测。

网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。

需要这份系统化的资料的朋友，可以添加V获取：vip204888 （备注大数据）

一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！

长的预测。

网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。

需要这份系统化的资料的朋友，可以添加V获取：vip204888 （备注大数据）
[外链图片转存中…(img-BGoKOt5R-1713367234970)]

2401_84166005

关注

24
点赞
踩
22

收藏

觉得还不错? 一键收藏
0
评论
一文速学数模-时序预测模型(一)灰色预测一文详解+Python实例代码_灰色关联度时序预测(1)

模型优点：数据少且无明显规律时可用，利用微分方程挖掘数据本质规律。模型缺点：灰色预测只适合短期预测、指数增长的预测。网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。需要这份系统化的资料的朋友，可以添加V获取：vip204888 （备注大数据）一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！
复制链接

扫一扫