2024年最全【算法】剑指offer-青蛙跳台阶&amp；&amp；矩形覆盖-CSDN博客

本文链接：https://blog.csdn.net/2401_84182020/article/details/138405568

文章讲述了如何使用动态规划解决用n个2*1小矩形无重叠覆盖2*n大矩形的问题，通过状态定义和递推关系f(n)=f(n-1)+f(n-2)，以及两种情况分析，最终给出了两种实现方式：使用数组dp存储状态或迭代计算斐波那契数列的值。

摘要由CSDN通过智能技术生成

    }
    if(number == 2)  
    {
        return 2;
    }
    int f1 = 1;//跳上第1级台阶的方法
    int f2 = 2;//跳上第2级台阶的方法
    int f3;
    //从跳上第三个台阶的方法数开始计算
    for(int i = 3;i<=number;i++)
    {
        f3 = f2+f1;
        f1 = f2;
        f2 = f3;
    }
    return f3;   
}

};

//写法2:
//从跳上第三个台阶的方法数开始计算
while(number>2)
{
f3 = f2+f1;
f1 = f2;
f2 = f3;
number–;
}
return f3;




---


### 矩形覆盖


我们可以用 2\*1 的小矩形横着或者竖着去覆盖更大的矩形.请问用n个 2\*1 的小矩形无重叠地覆盖一个 2\*n 的大矩形,总共有多少种方法？


比如n=3时, 2\*3 的矩形块有3种覆盖方法:


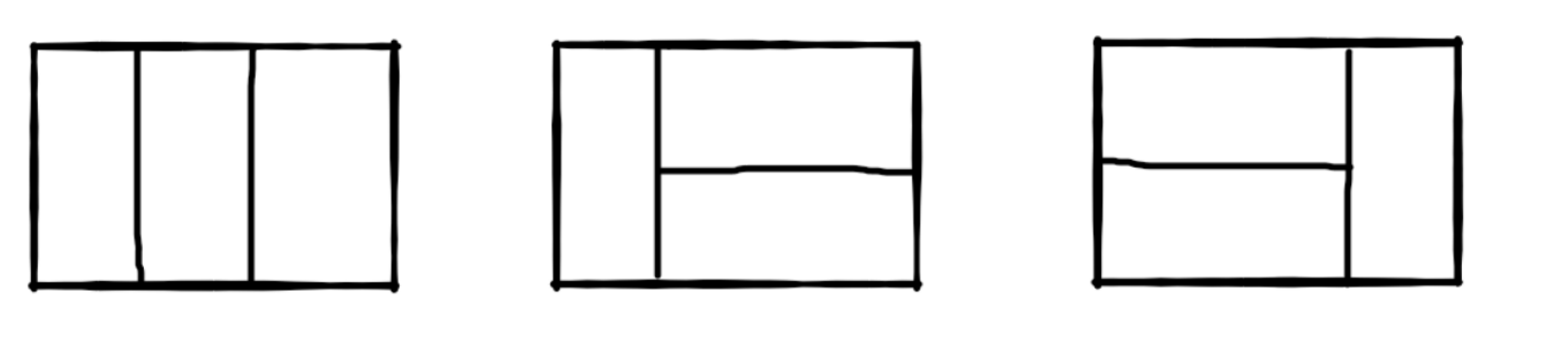
![image-20220405093847010](https://img-blog.csdnimg.cn/img_convert/d3d6358405eaeb1fcfe00ec8ab155a8a.png)

用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形
每次放置的时候,无非两种放法,横着放或竖着放:
其中,横着放一个之后,下一个的放法也就确定了,故虽然放置了两个矩形,但属于同一种放法,如果横着放一个,下一个必定也要横着放,所以要依次横着放两个
其中,竖着放一个之后,本轮放置也就完成了,也属于一种方法
所以,当2*n的大矩形被放满的时候,它无非就是从上面两种放置方法放置来的
我们继续使用dp来进行处理,当然后续会发现,斐波那契数列的方式也可以处理


状态定义:f(n) : 用n个2\*1的小矩形无重叠地覆盖一个2\*n的大矩形所用的**总方法数**  
 状态递推:f(n) = f(n-1)【最后一个竖着放】 + f(n-2)【最后两个横着放】  
 初始化:f(1) = 1,f(2) = 2,f(0)=0, 注意f(0)我们这个可以不考虑,题目说了,约定 n == 0 时,输出 0




| 表达式 | 含义 |
| --- | --- |
| f(n) | 用2\*1的小矩形无重叠的覆盖一个2\*n的大矩形的总方法数 |
| f(n-1) | 用2\*1的小矩形无重叠的覆盖一个2\*(n-1)的大矩形的总方法数 |
| f(n-2) | 用2\*1的小矩形无重叠的覆盖一个2\*(n-2)的大矩形的总方法数 |




---


情况1:要覆盖一个2\*n的矩形, 若我们规定最后一个放置的小矩形是竖着放的,那么覆盖该大矩形的覆盖总方法数就等于覆盖2\*(n-1)的大矩形的总方法数


![image-20220531175233580](https://img-blog.csdnimg.cn/img_convert/1ba96d3765bf270668413931f1fefdb2.png)




---


情况2:要覆盖一个2\*n的矩形, 若我们规定最后一个放置的小矩形是横着放的->则倒数第二个也一定要是横着放的,那么覆盖该大矩形的覆盖总方法数就等于覆盖2\*(n-2)的大矩形的总方法数


![image-20220531175213141](https://img-blog.csdnimg.cn/img_convert/26f20726ee8ad00a90af7156d9bc362d.png)




---


而实际覆盖的时候,我们不知道最后一个是竖着放还是横着放的,所以覆盖总方法数应该是这两种情况的方法数之和


->`f(n) = f(n-1)+f(n-2)`

class Solution {
public:
int rectCover(int number) {
//number = 0,1,2
if(number <=2)
{
return number;
}

    //f(n) : 用n个2\*1的小矩形无重叠地覆盖一个2\*n的大矩形所用的总方法数
    //f(n) = f(n-1)【最后一个竖着放】 + f(n-2)【最后两个横着放】
    
    //多开辟一个空间,让方法数和下标对应
    int\* dp = new int[number+1];
    dp[1] = 1;
    dp[2] = 2;
    for(int i =3;i<=number;i++)
    {
        dp[i] = dp[i-1]+dp[i-2];
    }
    int ans = dp[number];//先记录的答案
    delete[] dp;//释放数组
    return ans;
}

};


同样我们可以用迭代的方法:(斐波那契数列)

class Solution {
public:
int rectCover(int number) {
//number = 0,1,2
if(number <=2)
{
return number;
}
int f1 = 1;
int f2 = 2;
int f3;
for(int i = 3;i<=number;i++)
{
f3 = f1+f2;
f1 = f2;
f2 = f3;
}