先自我介绍一下,小编浙江大学毕业,去过华为、字节跳动等大厂,目前阿里P7
深知大多数程序员,想要提升技能,往往是自己摸索成长,但自己不成体系的自学效果低效又漫长,而且极易碰到天花板技术停滞不前!
因此收集整理了一份《2024年最新网络安全全套学习资料》,初衷也很简单,就是希望能够帮助到想自学提升又不知道该从何学起的朋友。






既有适合小白学习的零基础资料,也有适合3年以上经验的小伙伴深入学习提升的进阶课程,涵盖了95%以上网络安全知识点,真正体系化!
需要体系化学习资料的朋友,可以加我V获取:vip204888 (备注网络安全)
由于文件比较多,这里只是将部分目录截图出来,全套包含大厂面经、学习笔记、源码讲义、实战项目、大纲路线、讲解视频,并且后续会持续更新
posRight = j;
}
}
rightEnd = posRight;
if (flag) {
break;
}
flag = true;// 标志重置!!!!!!!!!!!!!!!!!!!!!!!!!
// 偶数轮,从右向左开始交换
for (int j = rightEnd; j > leftEnd; j--) {
if (arr[j] < arr[j - 1]) {
temp = arr[j];
arr[j] = arr[j - 1];
arr[j - 1] = temp;
flag = false;
posLeft = j;
}
}
leftEnd = posLeft;
if (flag) {
break;
}
}
}
## 选择排序及其优化
/**
* @param arr 选择排序
*/
public static void selectionSort(int[] arr) {
// 最开始,无序区间[0...n] 有序区间[]
// 当无序区间只剩下一个元素时,整个集合已经有序
for (int i = 0; i < arr.length - 1; i++) {
// min变量存储了当前的最小值索引
int min = i;
// 从剩下的元素中选择最小值
for (int j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[min]) {
min = j;
}
}
// min这个索引一定对应了当前无序区间中找到的最小值索引,换到无序区间最前面i
swap(arr,min,i);
}
}
**优化点:一次排序过程中同时选出最大值和最小值,放在无序区间的最后和最前**
/**
* @param arr 双向选择排序
*/
public static void selectionSortOP(int[] arr) {
int low = 0;
int high = arr.length - 1;//[low,high]表示整个无序区间
// low = high,无序区间只剩下一个元素,整个数组已经有序
while (low <= high) {
int min = low;
int max = low;
for (int i = low + 1; i <= high; i++) {
if (arr[i] < arr[min]) {
min = i;
}
if (arr[i] > arr[max]) {
max = i;
}
}
// min索引一定是当前无序区间的最小值索引,与low交换位置
swap(arr,low,min);
if (max == low) {//这个代码非常重要!!!!!!!!!!
// 最大值已经被换到min这个位置
max = min;
}
swap(arr,max,high);
low += 1;
high -= 1;
}
}
## 插入排序及其优化
\* 每次从无序区间中拿第一个值插入到已经排序区间的合适位置,直到整个数组有序
\* 在近乎有序的数据测试中,插入排序的性能好
\* 极端情况下,当集合是一个(完全/近乎)有序的集合,插入排序内层循环一次都不走~~~
\* 插入排序变为O(N);因此,插入排序经常作为高阶排序算法的优化手段之一
\* 插入排序是稳定的;arr[j] >= arr[j - 1]就停止了;相等的元素不会交换顺序,arr[j] < arr[j - 1]才交换
/**
* @param arr 直接插入排序
*/
public static void insertionSort(int[] arr) {
// 已排序区间[0,i)
// 待排序区间[i...n]
for (int i = 1; i < arr.length; i++) {
// 待排序区间的第一个元素arr[i]
// 从待排序区间的第一个元素向前看,找到合适的插入位置
// for (int j = i; j > 0; j–) {
// // arr[j - 1]已排序区间的最后一个元素
// if (arr[j] >= arr[j - 1]) {
// // 相等我们也不交换,保证稳定性
// // 此时说明arr[j] > 已排序区间的最大值,arr[j]已经有序了~~直接下次循环
// break;
// }else {
// swap(arr,j,j - 1);
// }
// }
for (int j = i; j > 0 && arr[j] < arr[j - 1]; j–) {
swap(arr,j,j - 1);
}
}
}
**优化点:因为插入排序中,每次都是在有序区间中选择插入位置 =>> 使用二分查找来定位元素的插入位置**
/**
* @param arr 折半插入排序
*/
public static void insertionSortBS(int[] arr) {
// 有序区间[0..i)
// 无序区间[i...n]
// i表示当前正在处理的元素,有序区间和无序区间的分界线就是i
for (int i = 1; i < arr.length; i++) {
int val = arr[i];
int left = 0;
int right = i;
while (left < right){
int mid = left + ((right - left) >> 1);
if (val < arr[mid]) {
right = mid;
}else {
// val >= arr[mid]
left = mid + 1;
}
}
// 搬移left..i的元素
for (int j = i; j > left; j--) {
arr[j] = arr[j - 1];
}
// left就是val插入的位置
arr[left] = val;
}
}
## 归并排序及其优化
**归并排序是一个稳定的nlogn排序算法**
**此处的稳定指的是时间复杂度稳定且归并排序也是一个稳定性排序算法**
**时间复杂度稳定:无论集合中的元素如何变化,归并排序的时间复杂度一直都是nlogn,不会退化为O(n^2)**
/**
* @param arr 未优化的归并排序
*/
public static void mergeSort(int[] arr) {
mergeSortInternal(arr,0,arr.length - 1);
}
/**
* 递归语义:在arr[l,r]进行归并排序,整个arr经过此函数后就是一个已经有序的数组
*/
private static void mergeSortInternal(int[] arr, int l, int r) {
if(l >= r){//左边的索引==右边的索引
return;
}
int mid = l + ((r - l) >> 1);
// 将原数组拆分为左右两个小区间,分别递归进行归并排序
// 走完这个函数之后 arr[l..mid]已经有序
mergeSortInternal(arr,l,mid);
// 走完这个函数之后 arr[mid + 1..r]已经有序
mergeSortInternal(arr,mid + 1,r);
//merge
merge(arr,l,mid,r);
}
/**
* 合并两个子数组arr[l,mid]和arr[mid + 1,r]
* 为一个大的有序数组arr[l,r]
*/
private static void merge(int[] arr, int l, int mid, int r) {
// 先创建一个新的临时数组aux
int[] aux = new int[r - l + 1];
// 将arr元素值拷贝到aux上
for (int i = 0; i < aux.length; i++) {
aux[i] = arr[i + l];
}
// i就是左侧小数组的开始索引
int i = l;
// j就是右侧小数组的开始索引
int j = mid + 1;
// k表示当前正在合并的原数组的索引下标
for (int k = l; k <= r; k++) {
if (i > mid) {
// 左侧区间已经被处理完毕,只需要将右侧区间的值拷贝原数组即可
arr[k] = aux[j - l];
j ++;
}else if (j > r) {
// 右侧区间已经被处理完毕,只需要将左侧区间的值拷贝到原数组即可
arr[k] = aux[i - l];
i ++;
}else if (aux[i - l] <= aux[j - l]) {
// 此时左侧区间的元素值较小,相等元素放在左区间,保证稳定性
arr[k] = aux[i - l];
i ++;
}else {
// 右侧区间的元素值较小
arr[k] = aux[j - l];
j ++;
}
}
}
**归并排序的两点优化:**
**1.当左右两个子区间走完子函数后,左右两个区间已经有序了;如果此时arr[mid] < arr[mid + 1]**
**arr[mid]已经是左区间的最大值;arr[mid + 1]已经是右区间的最小值 => 整个区间已经有序了,没必要再执行merge过程**
**2.在小区间上,可以直接俄使用插入排序来优化,没必要元素一致拆分到1位置;r - l <= 15,使用插入排序性能是很好的。可以减少归并的递归次数**
public static void mergeSort(int[] arr) {
mergeSortInternal(arr,0,arr.length - 1);
}
/**
* 在arr[l,r]进行归并排序,整个arr经过此函数后就是一个已经有序的数组
* 时间复杂度分析:
* 递归的深度就是拆分数组所用的时间,就是树的高度(logN)
* 合并两个子数组的过程merge;就是一个数组的遍历过程:O(n)
*/
private static void mergeSortInternal(int[] arr, int l, int r) {
if (r - l <= 15) {
// 优化2.小区间直接使用插入排序
insertionSort(arr,l,r);
return;
}
int mid = l + ((r - l) >> 1);
// 将原数组拆分为左右两个小区间,分别递归进行归并排序
// 走完这个函数之后 arr[l..mid]已经有序
mergeSortInternal(arr,l,mid);
// 走完这个函数之后 arr[mid + 1..r]已经有序
mergeSortInternal(arr,mid + 1,r);
// 优化1.只有左右两个子区间还有先后顺序不同时才merge
if (arr[mid] > arr[mid + 1]) {
merge(arr,l,mid,r);
}
}
/**
* 合并两个子数组arr[l,mid]和arr[mid + 1,r]
* 为一个大的有序数组arr[l,r]
*
为啥合并过程需要创建一个临时temp数组呢?
防止在合并的过程中,因为小元素覆盖大的元素,丢失某些元素
*/
private static void merge(int[] arr, int l, int mid, int r) {
// 先创建一个新的临时数组temp
int[] temp = new int[r - l + 1];
// 将arr元素值拷贝到temp上
for (int i = 0; i < temp.length; i++) {
temp[i] = arr[i + l];
}
// i就是左侧小数组的开始索引
int i = l;
// j就是右侧小数组的开始索引
int j = mid + 1;
// k表示当前正在合并的原数组的索引下标
for (int k = l; k <= r; k++) {
if (i > mid) {
// 左侧区间已经被处理完毕,只需要将右侧区间的值拷贝原数组即可
arr[k] = temp[j - l];
j ++;
}else if (j > r) {
// 右侧区间已经被处理完毕,只需要将左侧区间的值拷贝到原数组即可
arr[k] = temp[i - l];
i ++;
}else if (temp[i - l] <= temp[j - l]) {
// 此时左侧区间的元素值较小,相等元素放在左区间,保证稳定性!!!
arr[k] = temp[i - l];
i ++;
}else {
// 右侧区间的元素值较小
arr[k] = temp[j - l];
j ++;
}
}
}
/**
* 在arr[l..r]使用插入排序
* 归并优化调用了这个方法
*/
private static void insertionSort(int[] arr, int l, int r) {
for (int i = l + 1; i <= r; i++) {
for (int j = i; j > l && arr[j] < arr[j - 1]; j--) {
swap(arr,j,j - 1);
}
}
}
## 快速排序及其优化
快速排序的**基本思想是**:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列
#### 快速排序的三个步骤:
1)选择基准:在待排序列中,按照某种方式挑出一个元素,作为 "基准"(pivot)
2)分割操作:以该基准在序列中的实际位置,把序列分成两个子序列。此时,在基准左边的元素都比该基准小,在基准右边的元素都比基准大
3)递归地对两个序列进行快速排序,直到序列为空或者只有一个元素。
### 优化一:优化选取基准点
对于分治算法,当每次划分时,算法若都能分成两个等长的子序列时,那么分治算法效率会达到最大。也就是说,基准的选择是很重要的。选择基准的方式决定了两个分割后两个子序列的长度,进而对整个算法的效率产生决定性影响。**最理想的方法是,选择的基准恰好能把待排序序列分成两个等长的子序列**
#### 两种选择基准的方法
方法(1):固定位置
思想:取序列的第一个或最后一个元素作为基准
注意:基本的快速排序选取第一个或最后一个元素作为基准。但是,这是一直很不好的处理方法。
思想:取序列的中间元素作为基准。

测试数据分析:如果输入序列是随机的,处理时间可以接受的。如果数组已经有序时,此时的分割就是一个非常不好的分割。因为每次划分只能使待排序序列减1,此时为最坏情况,快速排序沦为起泡排序,时间复杂度为O(n^2)。而且,输入的数据是有序或部分有序的情况是相当常见的。因此,使用某一个元素作为枢纽元是非常糟糕的,为了避免这个情况,就引入了下面两个获取基准的方法。
方法(2):随机选取基准
引入的原因:在待排序列是部分有序时,固定选取枢轴使快排效率底下,要缓解这种情况,就引入了随机选取枢轴
思想:取待排序列中任意一个元素作为基准
int pivot = (int) (Math.random() * (r - l + 1)) + 1;
测试数据分析::这是一种相对安全的策略。由于枢轴的位置是随机的,那么产生的分割也不会总是会出现劣质的分割。在整个数组数字全相等时,仍然是最坏情况,时间复杂度是O(n^2)。实际上,随机化快速排序得到理论最坏情况的可能性仅为1/(2^n)。所以随机化快速排序可以对于绝大多数输入数据达到O(nlogn)的期望时间复杂度。
方法(3):三数取中(median-of-three)
分析:最佳的划分是将待排序的序列分成等长的子序列,最佳的状态我们可以使用序列的中间的值,也就是第N/2个数。可是,这很难算出来,并且会明显减慢快速排序的速度。这样的中值的估计可以通过随机选取三个元素并用它们的中值作为枢纽元而得到。事实上,随机性并没有多大的帮助,因此一般的做法是使用左端、右端和中心位置上的三个元素的中值作为枢纽元。显然使用三数中值分割法消除了预排序输入的不好情形**,并且减少快排大约14%的比较次数**
举例:待排序序列为:8 1 4 9 6 3 5 2 7 0
左边为:8,右边为0,中间为6.
我们这里取三个数排序后,中间那个数作为枢轴,则枢轴为6
注意:在选取中轴值时,可以从由左中右三个中选取扩大到五个元素中或者更多元素中选取,一般的,会有(2t+1)平均分区法(median-of-(2t+1),三平均分区法英文为median-of-three)。
具体思想:对待排序序列中low、mid、high三个位置上数据进行排序,取他们中间的那个数据作为枢轴,并用0下标元素存储枢轴。
即:采用三数取中,并用0下标元素存储枢轴。
/**
* @return 取待排序序列中left、mid、right三个位置上数据,选取他们中间的那个数据作为枢轴
*/
public static int SelectPivotMedianOfThree(int arr[], int left, int right) {
int temp = 0;
int mid = left + ((right - left) >> 1);// 计算数组中间元素的元素的下标
// 使用三数取中法选择枢轴
if (arr[mid] > arr[right]) {// 目标:arr[mid] <= arr[right]
temp = arr[mid];
arr[mid] = arr[right];
arr[right] = temp;
}
if (arr[left] > arr[right]) {// 目标:arr[left] <= arr[right]
temp = arr[left];
arr[left] = arr[right];
arr[right] = temp;
}
if (arr[mid] > arr[left]) {// 目标:arr[left] <= arr[mid]
temp = arr[mid];
arr[mid] = arr[left];
arr[left] = temp;
}
// 此时,arr[mid] <= arr[left] <= arr[right]
// left的位置上保留这三个位置上大小为中间的值
return arr[left];
}

**测试数据分析:使用三数取中选择枢轴优势还是很明显的,但是还是处理不了重复数组**
### 优化二:**当待排序序列的长度分割到一定大小后,使用插入排序**
原因:对于很小和部分有序的数组,快排不如插排好。当待排序序列的长度分割到一定大小后,继
续分割的效率比插入排序要差,此时可以使用插排而不是快排
截止范围:待排序序列长度N = 10,虽然在5~20之间任一截止范围都有可能产生类似的结果,这
种做法也避免了一些有害的退化情形。摘自《数据结构与算法分析》Mark Allen Weiness 著
if (right - left + 1 < 10) {
insertSort(arr);
return;
}
//else正常的快速排序

测试数据分析:针对随机数组,使用三数取中选择枢轴+插排,效率还是可以提高一点,真是针对已排序的数组,是没有任何用处的。因为待排序序列是已经有序的,那么每次划分只能使待排序序列减一。此时,插排是发挥不了作用的。所以这里看不到时间的减少。另外,三数取中选择枢轴+插排还是不能处理重复数组
### 优化三:三路快速排序
lt:less than gt:geater than

将数组划分为大于v、小于v、等于v三部分;l表示小于v部分的第一个元素,r表示大于v部分的最后一个元素;因此:arr[l + 1,lt]这部分表示的是所有小于v的元素;arr[lt + 1,i - 1]表示等于v的元素;arr[gt,r] 表示的是大于v这部分元素;i表示当前遍历到的元素;这样,就把要遍历的数据划分好了;现在的主要问题是,划分成这样的区间后,面对一个新的元素,我们应该做咋样的操作?
1)如果e == v ;就将e融入到等于v的这部分元素中,融入的方式就是i++;

2)如果是e < v ;只需要将e和等于v部分的第一个元素交换位置即可;交换完位置后,e就位于小于v部分的后面了;这样做的意义就是为了让e融入小于v部分的元素,融入的方式就是lt++;之后i++,来看下一个元素



3)如果 e > v ;只需要将此元素与大于v部分的前一个元素交换位置即可。此时,原来的大于v部分的前一个元素是还没被遍历的元素,交换后,把它放在了i所指的位置,而e就已经紧挨着大于v这部分元素了,这时将e融入到这部分元素即可,操作为gt--;然后将i++;因为之前交换后,给i所指向的位置挪过来一个未遍历的元素,此时,只需要继续判断这个元素就好了



最终,使用以上的方式一直进行下去,原始的数据就被分成了三部分,终止条件是i == gt,表示当前已经遍历完了所有的元素;然后,还要将v这个元素和lt指向的元素交换一下位置,这样;lt左边的元素都是小于v的元素,右边都是大于等于v的元素;v和等于v这部分元素融为一体,就不需要考虑等于v这部分元素了;下一步,只需要递归的对大于v和小于v这部分元素进行快速排序即可;三路排序的优点:不用考虑重复元素,极端情况下,如果要排序的数据元素全部相等,只需要一轮三路快排,就可以将所有元素全部排列有序。**此时,时间复杂度进化为O(n)。三路快排能够非常好的处理有大量重复元素的数据,同时对于近乎有序的数据和完全无序的数据效果也很好。是很多语言标准库中排序算法的底层实现。Java就是这样**




/**
* @param arr 三路快排
*/
public static void quickSort3(int[] arr) {
Random rnd = new Random();
partition3(arr,0,arr.length - 1,rnd);
}
private static void partition3(int[] arr, int l, int r,Random rnd) {
if (r - l <= 15) {
insertionSort(arr,l,r);
return;
}
//生成[l,r]之间的随机索引
int p = l + rnd.nextInt(r - l + 1);
swap(arr,l,p);
int v = arr[l];
// 这些变量的取值,一定是满足区间的定义,最开始的时候,所有区间都是空
// arr[l + 1..lt] < v
// lt是指向最后一个<v的元素
int lt = l;
// arr[lt + 1..i) == v
// i - 1是最后一个 = v的元素
int i = lt + 1;
// arr[gt..r] > v
// gt是第一个 > v的元素
int gt = r + 1;
// i从前向后扫描和gt重合时,所有元素就处理完毕
while (i < gt) {
if (arr[i] < v) {
// arr[l + 1..lt] < v
// arr[lt + 1..i) == v
swap(arr,i,lt + 1);
i ++;
lt ++;
}else if (arr[i] > v) {
// 交换到gt - 1
swap(arr,i,gt - 1);
gt --;
// 此处i不++,交换来的gt - 1还没有处理
}else {
// 此时arr[i] = v
i ++;
}
}
// lt落在最后一个 < v的索引处
swap(arr,l,lt);
// arr[l..lt - 1] < v
partition3(arr,l,lt - 1,rnd);
// arr[gt..r] > v
partition3(arr,gt,r,rnd);
}
### 优化四:尾递归排序
快排函数在函数尾部有两次递归操作,我们可以对其使用尾递归优化
### 如何自学黑客&网络安全
#### 黑客零基础入门学习路线&规划
**初级黑客**
**1、网络安全理论知识(2天)**
①了解行业相关背景,前景,确定发展方向。
②学习网络安全相关法律法规。
③网络安全运营的概念。
④等保简介、等保规定、流程和规范。(非常重要)
**2、渗透测试基础(一周)**
①渗透测试的流程、分类、标准
②信息收集技术:主动/被动信息搜集、Nmap工具、Google Hacking
③漏洞扫描、漏洞利用、原理,利用方法、工具(MSF)、绕过IDS和反病毒侦察
④主机攻防演练:MS17-010、MS08-067、MS10-046、MS12-20等
**3、操作系统基础(一周)**
①Windows系统常见功能和命令
②Kali Linux系统常见功能和命令
③操作系统安全(系统入侵排查/系统加固基础)
**4、计算机网络基础(一周)**
①计算机网络基础、协议和架构
②网络通信原理、OSI模型、数据转发流程
③常见协议解析(HTTP、TCP/IP、ARP等)
④网络攻击技术与网络安全防御技术
⑤Web漏洞原理与防御:主动/被动攻击、DDOS攻击、CVE漏洞复现
**5、数据库基础操作(2天)**
①数据库基础
②SQL语言基础
③数据库安全加固
**6、Web渗透(1周)**
①HTML、CSS和JavaScript简介
②OWASP Top10
③Web漏洞扫描工具
④Web渗透工具:Nmap、BurpSuite、SQLMap、其他(菜刀、漏扫等)
恭喜你,如果学到这里,你基本可以从事一份网络安全相关的工作,比如渗透测试、Web 渗透、安全服务、安全分析等岗位;如果等保模块学的好,还可以从事等保工程师。薪资区间6k-15k
到此为止,大概1个月的时间。你已经成为了一名“脚本小子”。那么你还想往下探索吗?
如果你想要入坑黑客&网络安全,笔者给大家准备了一份:282G全网最全的网络安全资料包评论区留言即可领取!
**7、脚本编程(初级/中级/高级)**
在网络安全领域。是否具备编程能力是“脚本小子”和真正黑客的本质区别。在实际的渗透测试过程中,面对复杂多变的网络环境,当常用工具不能满足实际需求的时候,往往需要对现有工具进行扩展,或者编写符合我们要求的工具、自动化脚本,这个时候就需要具备一定的编程能力。在分秒必争的CTF竞赛中,想要高效地使用自制的脚本工具来实现各种目的,更是需要拥有编程能力.
如果你零基础入门,笔者建议选择脚本语言Python/PHP/Go/Java中的一种,对常用库进行编程学习;搭建开发环境和选择IDE,PHP环境推荐Wamp和XAMPP, IDE强烈推荐Sublime;·Python编程学习,学习内容包含:语法、正则、文件、 网络、多线程等常用库,推荐《Python核心编程》,不要看完;·用Python编写漏洞的exp,然后写一个简单的网络爬虫;·PHP基本语法学习并书写一个简单的博客系统;熟悉MVC架构,并试着学习一个PHP框架或者Python框架 (可选);·了解Bootstrap的布局或者CSS。
**8、超级黑客**
这部分内容对零基础的同学来说还比较遥远,就不展开细说了,附上学习路线。
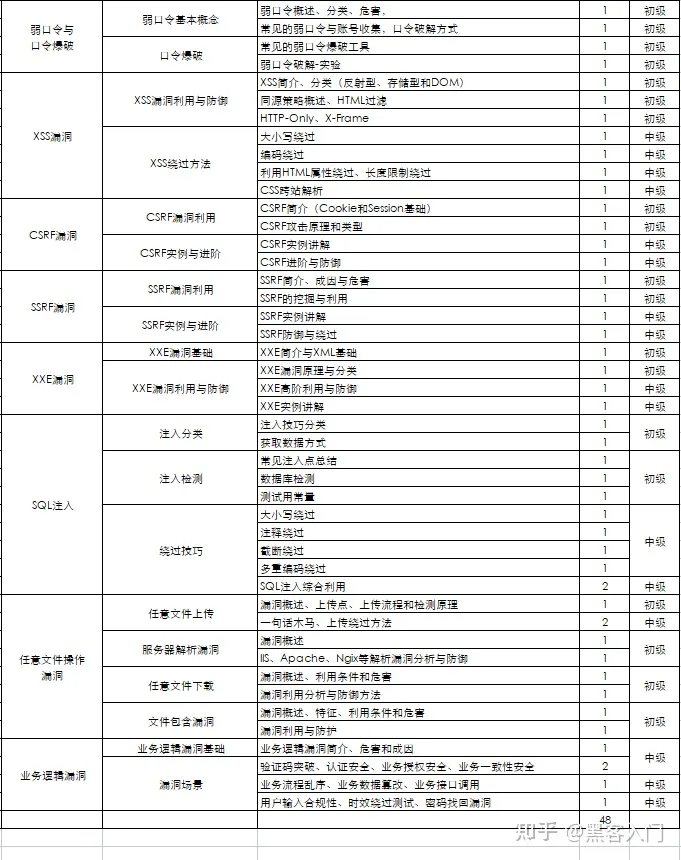
#### 网络安全工程师企业级学习路线

如图片过大被平台压缩导致看不清的话,评论区点赞和评论区留言获取吧。我都会回复的
视频配套资料&国内外网安书籍、文档&工具
**需要体系化学习资料的朋友,可以加我V获取:vip204888 (备注网络安全)**
当然除了有配套的视频,同时也为大家整理了各种文档和书籍资料&工具,并且已经帮大家分好类了。

一些笔者自己买的、其他平台白嫖不到的视频教程。
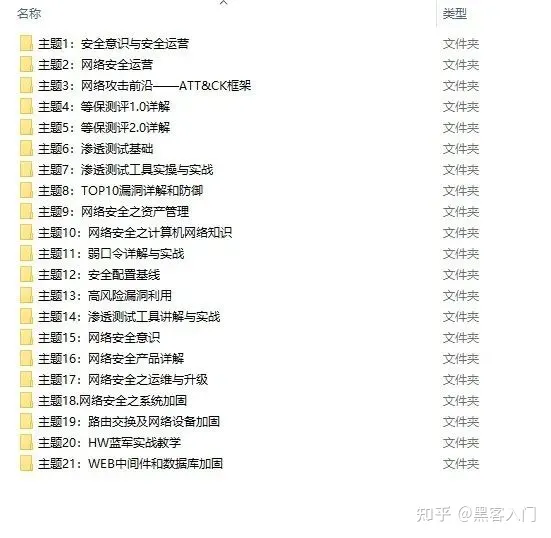
**网上学习资料一大堆,但如果学到的知识不成体系,遇到问题时只是浅尝辄止,不再深入研究,那么很难做到真正的技术提升。**
**[需要这份系统化资料的朋友,可以点击这里获取](https://bbs.csdn.net/topics/618540462)**
**一个人可以走的很快,但一群人才能走的更远!不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人,都欢迎加入我们的的圈子(技术交流、学习资源、职场吐槽、大厂内推、面试辅导),让我们一起学习成长!**
ebp?x-oss-process=image/format,png)
如图片过大被平台压缩导致看不清的话,评论区点赞和评论区留言获取吧。我都会回复的
视频配套资料&国内外网安书籍、文档&工具
**需要体系化学习资料的朋友,可以加我V获取:vip204888 (备注网络安全)**
当然除了有配套的视频,同时也为大家整理了各种文档和书籍资料&工具,并且已经帮大家分好类了。

一些笔者自己买的、其他平台白嫖不到的视频教程。

**网上学习资料一大堆,但如果学到的知识不成体系,遇到问题时只是浅尝辄止,不再深入研究,那么很难做到真正的技术提升。**
**[需要这份系统化资料的朋友,可以点击这里获取](https://bbs.csdn.net/topics/618540462)**
**一个人可以走的很快,但一群人才能走的更远!不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人,都欢迎加入我们的的圈子(技术交流、学习资源、职场吐槽、大厂内推、面试辅导),让我们一起学习成长!**























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








