Go最全高精度算法详解，零基础如何成为高级Golang开发

既有适合小白学习的零基础资料，也有适合3年以上经验的小伙伴深入学习提升的进阶课程，涵盖了95%以上Go语言开发知识点，真正体系化！

由于文件比较多，这里只是将部分目录截图出来，全套包含大厂面经、学习笔记、源码讲义、实战项目、大纲路线、讲解视频，并且后续会持续更新

如果你需要这些资料，可以戳这里获取

if (t) C.push\_back(t);
return C;

}

int main()
{
string a, b;
vector A, B;
cin >> a >> b;
for (int i = a.size() - 1; i >= 0; i – ) A.push_back(a[i] - ‘0’);
for (int i = b.size() - 1; i >= 0; i – ) B.push_back(b[i] - ‘0’);

auto C = add(A, B);

// 整个过程都是逆序存储的，因此最后输出时也需要倒序输出。
for (int i = C.size() - 1; i >= 0; i -- ) cout << C[i];
cout << endl;

return 0;

}

模板说明


该模板采用了递归调用

vector add(vector &A, vector &B)
{
if (A.size() < B.size()) return add(B, A);

vector<int> C;
int t = 0;//进位
for (int i = 0; i < A.size(); i ++ )
{
    t += A[i];
    if (i < B.size()) t += B[i];
    C.push\_back(t % 10);
    t /= 10;
}
//最后看最高位有没有1，若是1的话就压入
if (t) C.push\_back(t);
return C;

}

此模板也可以换种写法

vector add(vector &A, vector &B)
{

vector<int> C;
int t = 0;//进位
for (int i = 0; i < A.size() || i < B.size(); i ++ )
{
    if (i < A.size()) t += A[i];
    if (i < B.size()) t += B[i];
    C.push\_back(t % 10);
    t /= 10;
}
//最后看最高位有没有1，若是1的话就压入
if (t) C.push\_back(t);
return C;

}

### 高精度减法


整数的存储同上


#### 计算过程


这里以下式为例


![image-20220911132646580](https://img-blog.csdnimg.cn/img_convert/6fefa92a05bdefd2e502ddb2146ddf42.png)


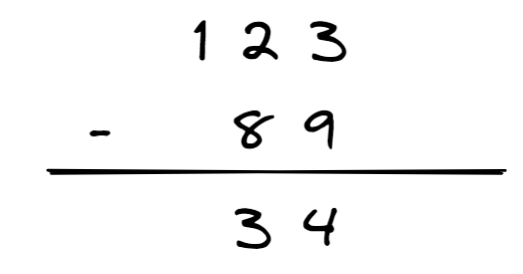
再次把它抽象一下，形成一下形式


![image-20220911133800828](https://img-blog.csdnimg.cn/img_convert/d96c3dc31ee216926a62061cf066eb50.png)


由此我们可以列出以下式子


首先判断A 与 B的关系，如果A 大于B，则正常加减，否则就计算其差的负数。


![image-20220911134113852](https://img-blog.csdnimg.cn/img_convert/ee38de7453b9feaa453138a1f1867c42.png)


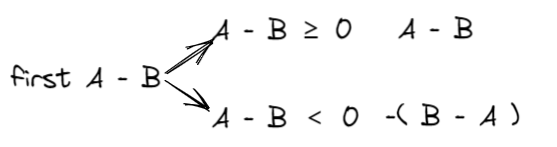
然后分别判断每一位的大小，并且计算是否需要进位。（减去下一位的借位，没借位则t是0，有借位则t是1）


如果是大于0的话，就直接减，如果是小于0的话，就借一位再减。


![image-20220911134506979](https://img-blog.csdnimg.cn/img_convert/99354298a011300c86952ca980198339.png)


#### 例题：高精度减法


给定两个正整数（不含前导 0），计算它们的差，计算结果可能为负数。


**输入格式**


共两行，每行包含一个整数。


**输出格式**


共一行，包含所求的差。


**数据范围**


1≤整数长度≤ 
 
 
 
 
 1 
 
 
 
 0 
 
 
 5 
 
 
 
 
 10^5 
 
 
 105


**输入样例：**

32
11

**输出样例：**

21

#### 算法模板

#include
#include

using namespace std;

//判断是否有A ≥ B
bool cmp(vector &A, vector &B)
{
//首先判断两个数的位数大小，设置return A > B
if (A.size() != B.size()) return A.size() > B.size();
// 位数相同，从最高位开始比较，设置return A > B
for (int i = A.size() - 1; i >= 0; i – )
if (A[i] != B[i])
return A[i] > B[i];
return true;
}

vector sub(vector &A, vector &B)
{
vector C;
for (int i = 0, t = 0; i < A.size(); i ++ )
{
// 倒序存储，因此实际上是从低位逐渐向高位遍历。
t = A[i] - t;
// 首先要判断以下B[i]是否存在
if (i < B.size()) t -= B[i];
// 本位，这里的(t + 10) % 10,如果t是0-9，则会抵消，如果t是小于0，则相当于是 +10 借位。
C.push_back((t + 10) % 10);
// t小于0，表示需要借位，因此标记为1，这样在传递到下一次循环（即前一位时会自动减1（减去借位））
if (t < 0) t = 1;
else t = 0;
}
//删除前导0
while (C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}

int main()
{
string a, b;
vector A, B;
cin >> a >> b;
for (int i = a.size() - 1; i >= 0; i – ) A.push_back(a[i] - ‘0’);
for (int i = b.size() - 1; i >= 0; i – ) B.push_back(b[i] - ‘0’);

vector<int> C;

if (cmp(A, B)) C = sub(A, B);
else C = sub(B, A), cout << '-';

for (int i = C.size() - 1; i >= 0; i -- ) cout << C[i];
cout << endl;

return 0;

}

### 高精度乘法


存储与上相同。


#### 计算过程


这里先列出计算式的通式


![image-20220911154058993](https://img-blog.csdnimg.cn/img_convert/c153e5c3fc068a6adb986deeed4b22ff.png)


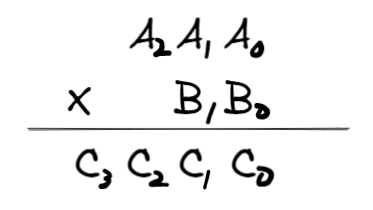
与常见的计算相似，每一位分别考虑进位和取余当前的数字


当前位： 
 
 
 
 
 
 C 
 
 
 0 
 
 
 
 = 
 
 
 ( 
 
 
 
 A 
 
 
 0 
 
 
 
 ∗ 
 
 
 
 B 
 
 
 1 
 
 
 
 
 B 
 
 
 0 
 
 
 
 + 
 
 
 t 
 
 
 ) 
 
 
 % 
 
 
 10 
 
 
 
 C\_0 = (A\_0 \* B\_1 B\_0 + t) \% 10 
 
 
 C0​=(A0​∗B1​B0​+t)%10


进位： 
 
 
 
 
 t 
 
 
 = 
 
 
 ( 
 
 
 
 A 
 
 
 0 
 
 
 
 ∗ 
 
 
 
 B 
 
 
 1 
 
 
 
 
 B 
 
 
 0 
 
 
 
 ) 
 
 
 / 
 
 
 10 
 
 
 
 t = (A\_0 \* B\_1 B\_0) / 10 
 
 
 t=(A0​∗B1​B0​)/10


注意：这里是把B看成一个整体，而不是和一般的乘法一样。这样b方便计算，同时也方便存储（直接存为int就行）。


#### 例题：高精度乘法


给定两个非负整数（不含前导 0） A 和 B，请你计算 A×B 的值。


**输入格式**


共两行，第一行包含整数 A，第二行包含整数 B。


**输出格式**


共一行，包含 A×B 的值。


**数据范围**


 
 
 
 
 
 1 
 
 
 ≤ 
 
 
 A 
 
 
 的长度 
 
 
 ≤ 
 
 
 100000 
 
 
 
 1≤A的长度≤100000 
 
 
 1≤A的长度≤100000,  
  
 
 
 
 
 0 
 
 
 ≤ 
 
 
 B 
 
 
 ≤ 
 
 
 10000 
 
 
 
 0≤B≤10000 
 
 
 0≤B≤10000


**输入样例：**

2
3

**输出样例：**

6

#### 算法模板

#include
#include

using namespace std;

vector mul(vector &A, int b)
{
vector C;

//进位
int t = 0;
for (int i = 0; i < A.size() || t; i ++ )
{
    if (i < A.size()) t += A[i] \* b;
    C.push\_back(t % 10);
    t /= 10;
}

while (C.size() > 1 && C.back() == 0) C.pop\_back();
return C;

}

int main()
{
string a;
int b;

cin >> a >> b;

vector<int> A;
for (int i = a.size() - 1; i >= 0; i -- ) A.push\_back(a[i] - '0');

auto C = mul(A, b);

for (int i = C.size() - 1; i >= 0; i -- ) printf("%d", C[i]);

return 0;

}

核心模板

if (i < A.size()) t += A[i] * b;
C.push_back(t % 10);
t /= 10;

### 高精度除法


#### 计算过程


高精度除法的通式如下：


![image-20220911165652347](https://img-blog.csdnimg.cn/img_convert/53c70294696c478076d0c65efcf6416e.png)


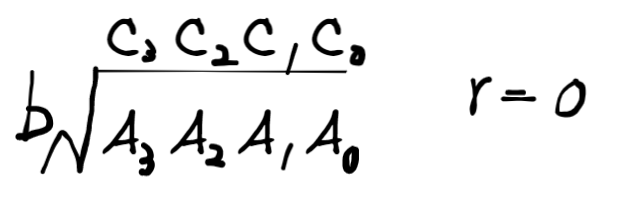
仿照求解除法的过程，可以设计高精度除法算法如下：


最开始余数r为0


（核心模板）


* r 
 
 
 = 
 
 
 r 
 
 
 ∗ 
 
 
 10 
 
 
 + 
 
 
 
 A 
 
 
 3 
 
 
 
 
 r = r \*10 + A \_3 
 
 
 r=r∗10+A3​
* C 
 
 
 3 
 
 
 
 = 
 
 
 ( 
 
 
 r 
 
 
 ∗ 
 
 
 10 
 
 
 + 
 
 
 
 A 
 
 
 3 
 
 
 
 ) 
 
 
 / 
 
 
 b 
 
 
 
 C\_3 = (r \*10 + A \_3) / b 
 
 
 C3​=(r∗10+A3​)/b ;
* r 
 
 
 = 
 
 
 r 
 
 
 % 
 
 
 b 
 
 
 
 r = r \% b 
 
 
 r=r%b


#### 例题：高精度除法


给定两个非负整数（不含前导 0） A，B，请你计算 A/B 的商和余数。


**输入格式**


共两行，第一行包含整数 A，第二行包含整数 B。


**输出格式**


共两行，第一行输出所求的商，第二行输出所求余数。


**数据范围**


 
 
 
 


![img](https://img-blog.csdnimg.cn/img_convert/748ea858eaa508ff5982d2b39c84b023.png)
![img](https://img-blog.csdnimg.cn/img_convert/96b6d2d0f7f43080bff336b5a19281c9.png)

**网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。**

**[需要这份系统化的资料的朋友，可以添加戳这里获取](https://bbs.csdn.net/topics/618658159)**


**一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！**

 
 3 
 
 
 
 ) 
 
 
 / 
 
 
 b 
 
 
 
 C\_3 = (r \*10 + A \_3) / b 
 
 
 C3​=(r∗10+A3​)/b ;
* r 
 
 
 = 
 
 
 r 
 
 
 % 
 
 
 b 
 
 
 
 r = r \% b 
 
 
 r=r%b


#### 例题：高精度除法


给定两个非负整数（不含前导 0） A，B，请你计算 A/B 的商和余数。


**输入格式**


共两行，第一行包含整数 A，第二行包含整数 B。


**输出格式**


共两行，第一行输出所求的商，第二行输出所求余数。


**数据范围**


 
 
 
 


[外链图片转存中...(img-Jdj0PtI8-1715512588224)]
[外链图片转存中...(img-dFmiODp9-1715512588224)]

**网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。**

**[需要这份系统化的资料的朋友，可以添加戳这里获取](https://bbs.csdn.net/topics/618658159)**


**一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！**