斜率优化dp
斜率优化动态规划(DP)是一种用于优化动态规划算法的高级技巧,主要用于加速特定类型动态规划问题的状态转移过程,
基本概念
动态规划:将复杂问题分解为子问题,通过求解子问题并保存结果来避免重复计算,从而解决原问题的算法策略。例如,斐波那契数列可以用动态规划求解,定义 (dp[n]=dp[n - 1]+dp[n - 2]) ,并保存 (dp[i]) 的值以避免重复计算。
斜率优化:在动态规划状态转移过程中,利用斜率的性质来快速确定最优决策点,从而减少状态转移的时间复杂度。它通常适用于状态转移方程具有特定形式的动态规划问题。
适用场景
状态转移方程具有凸性或凹性:当动态规划的状态转移方程满足一定的凸性或凹性条件时,斜率优化往往可以发挥作用。例如,状态转移方程形如 (dp[i]=min_{0<= j < i}{dp[j]+cost(j, i)}) ,其中 (cost(j, i)) 是从状态 (j) 转移到状态 (i) 的代价,且 (cost(j, i)) 关于 (j) 和 (i) 的某种函数关系呈现凸性或凹性。
决策单调性:即随着状态 (i) 的增大,最优决策点 (j) 单调变化。例如,若对于 (i_1 < i_2) ,状态 (i_1) 的最优决策点为 (j_1) ,状态 (i_2) 的最优决策点为 (j_2) ,则 (j_1<= j_2) (或 (j_1geq j_2) )。
优化原理
对于满足上述条件的动态规划问题,通过将状态转移方程进行变形,可以将其转化为与斜率相关的表达式。在平面直角坐标系中,每个状态 (j) 可以看作一个点 ((x_j, y_j)) ,其中 (x_j) 和 (y_j) 是根据状态转移方程和问题特性定义的坐标。通过分析不同点之间连线的斜率与最优决策点的关系,利用单调队列等数据结构维护这些点,使得在寻找最优决策点时可以通过比较斜率快速确定,从而避免对所有可能决策点的遍历,将状态转移的时间复杂度从 (O(n)) 降低到接近 (O(1)) 。
实现步骤
1. 确定状态和状态转移方程:根据问题定义动态规划的状态 (dp[i]) ,并写出状态转移方程,例如 (dp[i]=min_{0<= j < i}{dp[j]+cost(j, i)}) 。
2. 变形状态转移方程:将状态转移方程变形为可以用斜率表示的形式。假设 (dp[i]) 的状态转移方程经过变形后为 (y_i = a_i x_j + b_j + c_i) (其中 (a_i) 、 (c_i) 只与 (i) 有关, (b_j) 只与 (j) 有关),那么不同决策点 (j_1) 和 (j_2) 对应的直线斜率 (k={b_{j_1}-b_{j_2}}/{x_{j_1}-x_{j_2}}) 。
3. 维护单调队列:使用单调队列维护决策点(即点 ((x_j, y_j)) )。新点入队时,根据斜率的单调性,将队尾不满足条件的点出队,保持队列的单调性。同时,当状态 (i) 变化时,可能需要从队首移除不再是最优决策点的点。
4. 确定最优决策点:根据状态转移方程变形后的斜率关系,从单调队列的队首获取当前状态 (i) 的最优决策点 (j) ,用于计算 (dp[i]) 。
5. 计算最终结果:按照动态规划的流程,依次计算出所有状态的 (dp) 值,最终得到问题的解。
示例
问题:给定一个序列 (a_1, a_2, ....., a_n) ,要求将其分成若干段,每段的代价为该段元素和的平方,求使得总代价最小的分段方案。
状态定义:设 (dp[i]) 表示将前 (i) 个元素进行分段的最小总代价。
状态转移方程: (dp[i]=min_{<=j < i}{dp[j]+(sum_{k = j + 1}^{i}a_k)^2}) 。令 (s[i]) 为序列的前缀和,即 (s[i]=sum_{k = 1}^{i}a_k) ,则状态转移方程可化为 (dp[i]=min_{0<= j < i}{dp[j]+(s[i]-s[j])^2}) 。
变形状态转移方程:展开 ((s[i]-s[j])^2) 得到 (dp[i]=min_{0<= j < i}{dp[j]+s[i]^2 - 2s[i]s[j]+s[j]^2}) 。设 (x_j = s[j]) , (y_j = dp[j]+s[j]^2) ,则 (dp[i]=s[i]^2 - 2s[i]x_j + y_j) ,这是一个关于 (x_j) 和 (y_j) 的线性表达式,不同决策点 (j) 对应的直线斜率 (k={y_{j_1}-y_{j_2}}/{x_{j_1}-x_{j_2}}) 。
维护单调队列:维护一个下凸壳(根据斜率性质)的单调队列,新的决策点 (j) 对应的点 ((x_j, y_j)) 入队时,通过比较斜率将队尾不满足下凸壳性质的点出队。
确定最优决策点:对于状态 (i) ,从单调队列的队首获取最优决策点 (j) ,计算 (dp[i]) 。
计算结果:计算出 (dp[n]) 即为将整个序列分段的最小总代价。
习题(任务安排1):

分析:
这是一道关于任务分组以最小化总费用的优化问题,核心在于在任务顺序固定的前提下,合
理划分任务批次,综合考虑任务执行时间、启动时间和费用系数来降低总费用
任务相关信息:有 个任务按顺序排列,执行第 个任务所需时间为 ,每个任务有对应的费
用系数 ,任务顺序不可改变。
分组与时间规则:机器将任务分成若干批,每批包含连续的若干任务。每批任务开始前机器
有启动时间 ,一批任务的执行时间是启动时间 加上该批内每个任务所需时间之和。同一批
任务在同一时刻完成,任务执行后在机器中等待直至该批任务全部执行完毕。
费用计算方式:每个任务的费用是其完成时刻乘以费用系数 。
任务目标:为机器规划分组方案,使总费用最小。
下面的图假设了s是1

伪代码1:
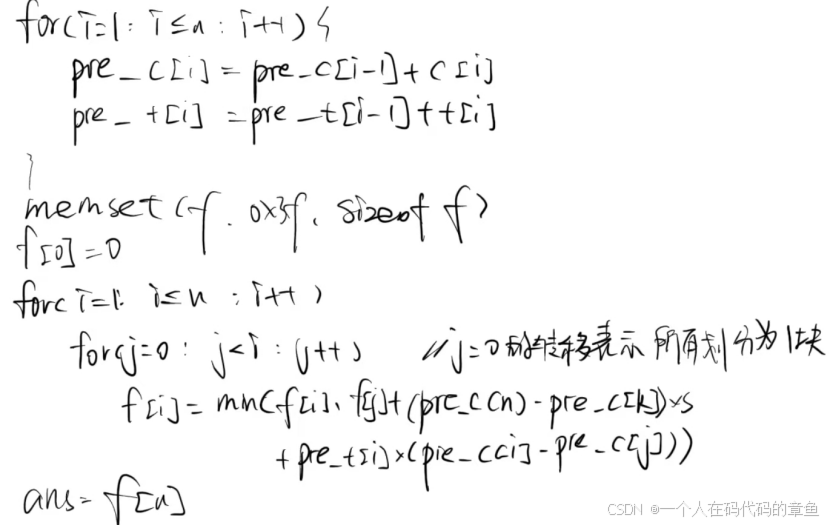
接下来思考如何去优化
习题2(进一步优化):


伪代码2:
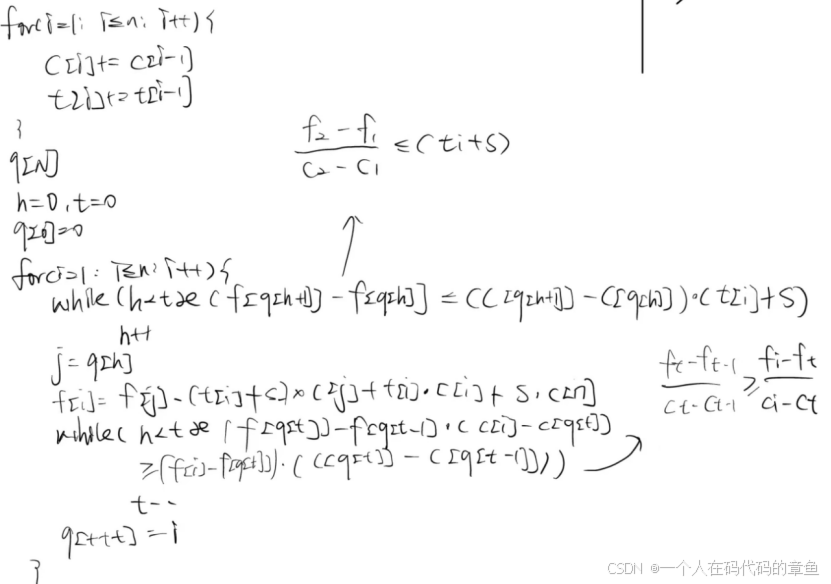
























 71
71

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








