


既有适合小白学习的零基础资料,也有适合3年以上经验的小伙伴深入学习提升的进阶课程,涵盖了95%以上Go语言开发知识点,真正体系化!
由于文件比较多,这里只是将部分目录截图出来,全套包含大厂面经、学习笔记、源码讲义、实战项目、大纲路线、讲解视频,并且后续会持续更新
{
if(n<=0)
return 0;
if(n==1)
return 1;
return fib( n-1)+fib(n-2);
}
//输入6
//输出:8
先来分析一下递归算法的执行流程,假如输入6,那么执行的递归树如下:
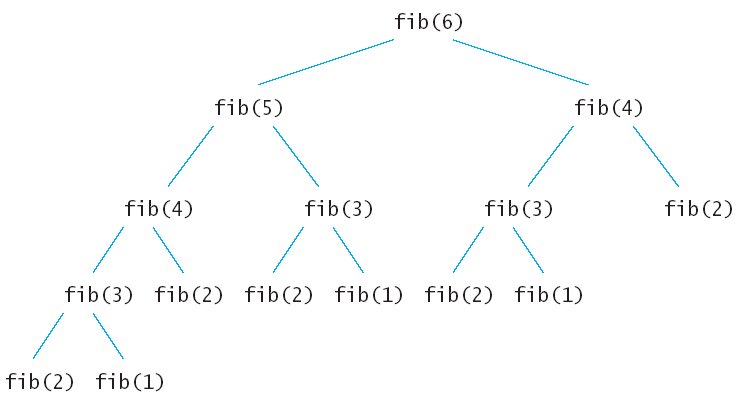
上面的递归树中的每一个子节点都会执行一次,很多重复的节点被执行,fib(2)被重复执行了5次。由于调用每一个函数的时候都要保留上下文,所以空间上开销也不小。这么多的子节点被重复执行,如果在执行的时候把执行过的子节点保存起来,后面要用到的时候直接查表调用的话可以节约大量的时间。下面就看看动态规划的两种方法怎样来解决斐波拉契数列\*\*Fibonacci \*\*数列问题。
### **①自顶向下的备忘录法**
public static int Fibonacci(int n)
{
if(n<=0)
return n;
int []Memo=new int[n+1];
for(int i=0;i<=n;i++)
Memo[i]=-1;
return fib(n, Memo);
}
public static int fib(int n,int []Memo)
{
if(Memo[n]!=-1)
return Memo[n];
//如果已经求出了fib(n)的值直接返回,否则将求出的值保存在Memo备忘录中。
if(n<=2)
Memo[n]=1;
else Memo[n]=fib( n-1,Memo)+fib(n-2,Memo);
return Memo[n];
}
备忘录法也是比较好理解的,创建了一个n+1大小的数组来保存求出的斐波拉契数列中的每一个值,在递归的时候如果发现前面fib(n)的值计算出来了就不再计算,如果未计算出来,则计算出来后保存在Memo数组中,下次在调用fib(n)的时候就不会重新递归了。比如上面的递归树中在计算fib(6)的时候先计算fib(5),调用fib(5)算出了fib(4)后,fib(6)再调用fib(4)就不会在递归fib(4)的子树了,因为fib(4)的值已经保存在Memo[4]中。
### **②自底向上的动态规划**
备忘录法还是利用了递归,上面算法不管怎样,计算fib(6)的时候最后还是要计算出fib(1),fib(2),fib(3)…,那么何不先计算出fib(1),fib(2),fib(3)…,呢?这也就是动态规划的核心,先计算子问题,再由子问题计算父问题。
public static int fib(int n)
{
if(n<=0)
return n;
int []Memo=new int[n+1];
Memo[0]=0;
Memo[1]=1;
for(int i=2;i<=n;i++)
{
Memo[i]=Memo[i-1]+Memo[i-2];
}
return Memo[n];
}
自底向上方法也是利用数组保存了先计算的值,为后面的调用服务。观察参与循环的只有 i,i-1 , i-2三项,因此该方法的空间可以进一步的压缩如下。
public static int fib(int n)
{
if(n<=1)
return n;
int Memo_i_2=0;
int Memo_i_1=1;
int Memo_i=1;
for(int i=2;i<=n;i++)
{
Memo_i=Memo_i_2+Memo_i_1;
Memo_i_2=Memo_i_1;
Memo_i_1=Memo_i;
}
return Memo_i;
}
一般来说由于备忘录方式的动态规划方法使用了递归,递归的时候会产生额外的开销,使用自底向上的动态规划方法要比备忘录方法好。
你以为看懂了上面的例子就懂得了动态规划吗?那就too young too simple了。动态规划远远不止如此简单,下面先给出一个例子看看能否独立完成。然后再对动态规划的其他特性进行分析。
### **动态规划小试牛刀**
**例题:钢条切割**
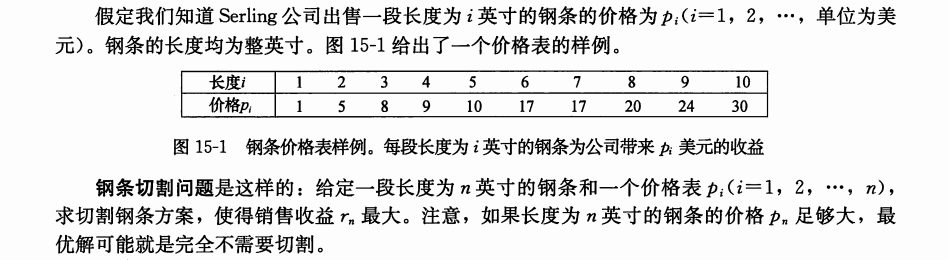
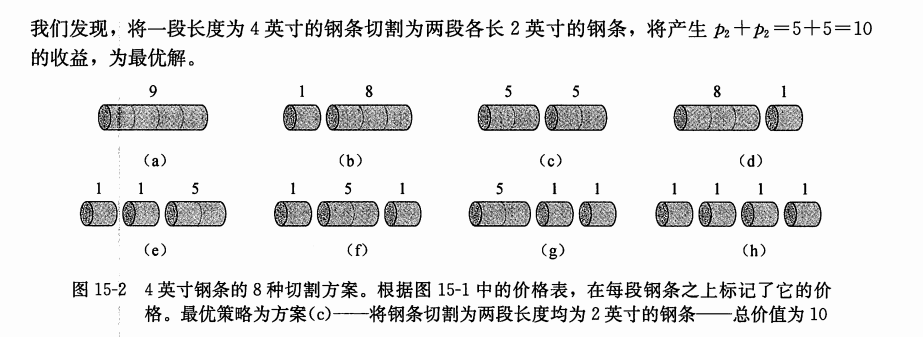


上面的例题来自于**算法导论**
关于题目的讲解就直接截图算法导论书上了这里就不展开讲。现在使用一下前面讲到三种方法来来实现一下。
**①递归版本**
public static int cut(int []p,int n)
{
if(n==0)
return 0;
int q=Integer.MIN_VALUE;
for(int i=1;i<=n;i++)
{
q=Math.max(q, p[i-1]+cut(p, n-i));
}
return q;
}
递归很好理解,如果不懂可以看上面的讲解,递归的思路其实和回溯法是一样的,遍历所有解空间但这里和上面斐波拉契数列的不同之处在于,在每一层上都进行了一次最优解的选择,q=Math.max(q, p[i-1]+cut(p, n-i));这个段语句就是最优解选择,这里上一层的最优解与下一层的最优解相关。
**②备忘录版本**
public static int cutMemo(int []p)
{
int []r=new int[p.length+1];
for(int i=0;i<=p.length;i++)
r[i]=-1;
return cut(p, p.length, r);
}
public static int cut(int []p,int n,int []r)
{
int q=-1;
if(r[n]>=0)
return r[n];
if(n==0)
q=0;
else {
for(int i=1;i<=n;i++)
q=Math.max(q, cut(p, n-i,r)+p[i-1]);
}
r[n]=q;
return q;
}
有了上面求斐波拉契数列的基础,理解备忘录方法也就不难了。备忘录方法无非是在递归的时候记录下已经调用过的子函数的值。这道钢条切割问题的经典之处在于自底向上的动态规划问题的处理,理解了这个也就理解了动态规划的精髓。
**③自底向上的动态规划**
public static int buttom_up_cut(int []p)
{
int []r=new int[p.length+1];
for(int i=1;i<=p.length;i++)
{
int q=-1;
//①
for(int j=1;j<=i;j++)
q=Math.max(q, p[j-1]+r[i-j]);
r[i]=q;
}
return r[p.length];
}
自底向上的动态规划问题中最重要的是理解注释①处的循环,这里外面的循环是求r[1],r[2]…,里面的循环是求出r[1],r[2]…的最优解,也就是说r[i]中保存的是钢条长度为i时划分的最优解,这里面涉及到了最优子结构问题,也就是一个问题取最优解的时候,它的子问题也一定要取得最优解。下面是长度为4的钢条划分的结构图。我就偷懒截了个图。
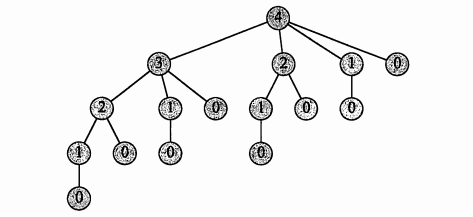
### **动态规划原理**
虽然已经用动态规划方法解决了上面两个问题,但是大家可能还跟我一样并不知道什么时候要用到动态规划。总结一下上面的斐波拉契数列和钢条切割问题,发现两个问题都涉及到了重叠子问题,和最优子结构。
**①最优子结构**
用动态规划求解最优化问题的第一步就是刻画最优解的结构,如果一个问题的解结构包含其子问题的最优解,就称此问题具有最优子结构性质。因此,某个问题是否适合应用动态规划算法,它是否具有最优子结构性质是一个很好的线索。使用动态规划算法时,用子问题的最优解来构造原问题的最优解。因此必须考查最优解中用到的所有子问题。
---
**②重叠子问题**
在斐波拉契数列和钢条切割结构图中,可以看到大量的重叠子问题,比如说在求fib(6)的时候,fib(2)被调用了5次,在求cut(4)的时候cut(0)被调用了4次。如果使用递归算法的时候会反复的求解相同的子问题,不停的调用函数,而不是生成新的子问题。如果递归算法反复求解相同的子问题,就称为具有重叠子问题(overlapping subproblems)性质。在动态规划算法中使用数组来保存子问题的解,这样子问题多次求解的时候可以直接查表不用调用函数递归。
## **动态规划的经典模型**
### **线性模型**
线性模型的是动态规划中最常用的模型,上文讲到的钢条切割问题就是经典的线性模型,这里的线性指的是状态的排布是呈线性的。【例题1】是一个经典的面试题,我们将它作为线性模型的敲门砖。
\*\*【例题1】\*\*在一个夜黑风高的晚上,有n(n <= 50)个小朋友在桥的这边,现在他们需要过桥,但是由于桥很窄,每次只允许不大于两人通过,他们只有一个手电筒,所以每次过桥的两个人需要把手电筒带回来,i号小朋友过桥的时间为T[i],两个人过桥的总时间为二者中时间长者。问所有小朋友过桥的总时间最短是多少。




**既有适合小白学习的零基础资料,也有适合3年以上经验的小伙伴深入学习提升的进阶课程,涵盖了95%以上Go语言开发知识点,真正体系化!**
**由于文件比较多,这里只是将部分目录截图出来,全套包含大厂面经、学习笔记、源码讲义、实战项目、大纲路线、讲解视频,并且后续会持续更新**
**[如果你需要这些资料,可以戳这里获取](https://bbs.csdn.net/topics/618658159)**
320)]
[外链图片转存中...(img-VX1d3dcI-1715790812321)]
**既有适合小白学习的零基础资料,也有适合3年以上经验的小伙伴深入学习提升的进阶课程,涵盖了95%以上Go语言开发知识点,真正体系化!**
**由于文件比较多,这里只是将部分目录截图出来,全套包含大厂面经、学习笔记、源码讲义、实战项目、大纲路线、讲解视频,并且后续会持续更新**
**[如果你需要这些资料,可以戳这里获取](https://bbs.csdn.net/topics/618658159)**






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








