目录
一、概述
机器学习,研究从数据中产生模型(model)的算法,即学习算法(learning algorithm)。
1. 一些术语
数据集(data set):所有数据记录组成的集合。
样本(sample):每一条记录的描述。
特征向量(feature vecotr):如果把样本的属性作为坐标轴,那么它张成的空间中,每个样本都能在其中找到其坐标位置。因此,一个样本又称为一个特征向量。
学习(learning)或训练(training):从数据中产生模型的过程,这一过程通过执行某个学习算法完成。也可以看做是在所有“假设”组成的空间中进行搜索的过程。
模型:学习产生的模型对应了数据的某种潜在规律,也称为“假设”(hypothesis)。
泛化能力(generalization):模型适用于新样本的能力。
监督学习(supervised learning):训练数据有标记,分类和回归问题是其代表。
无监督学习(unsupervised learning):训练数据没有有标记,聚类问题是其代表。
过拟合(overfitting):把训练样本的特殊性质作为了所有潜在样本的一般性质。
欠拟合(underfitting):与过拟合相对,对训练样本的一般性质为学习好。
误差(error):模型的预测输出与样本的真实输出之间的差异。模型在训练集上的误差称为训练误差;在新样本上的误差称为泛化误差。
2. 归纳偏好
模型对应了假设空间中的一个假设。有多个模型符合要求时,机器学习通过对某种类型的假设的偏好来确定结果,这称为归纳偏好。任何一个有效的机器学习算法必有其归纳偏好。
3. 验证模型
通常通过测试模型的泛化误差来选择模型。以测试集上的测试误差来作为泛化误差的近似。
3.1 留出法
将数据集划分为两个互斥的集合,一个作为训练集,另一个作为测试集。对训练/测试集的划分,要尽量保存数据分布的一致性(从采样的角度看,保留类别比例,称为分层采样)。
单次留出法的结果不稳定,可以多次随机划分、重复实验取平均值。
通常是将2/3-4/5的样本用于训练,剩余用于测试。
3.2 交叉验证法
通过分层采样,将数据集D划分为k个大小相似的互斥子集,每次采用k-1个子集作为训练集,剩下的一个作为测试集。(k折交叉验证)
4 性能度量
衡量模型泛化能量的评估标准。
4.1 错误率与精度
4.2 查准率、查全率
4.3 代价敏感错误率
5 比较
如何对模型进行比较?
比较两个模型的误差的大小?比较误差的方差?
6 偏差与方差
偏差,度量了模型的期望预测与真实结果的偏离程度,即拟合能力,
方差,度量了同样大小的训练集的变动所导致的学习性能的变化,即数据扰动所造成的影响,
噪声,度量了在当前任务上任何学习算法所能达到的期望泛化误差的下界,即问题本身的难度,
偏差-方差分解说明,泛化性能是由学习算法的能力、数据的充分性以及学习任务本身的难度同决定。给定学习任务,为了取得好的泛化性能,则需使偏差较小,即能够充分拟合数据;使方差较小,即使得数据扰动产生的影响小。
二、线性模型
d个属性的样本,习得通过属性的线性组合进行预测的函数。
1. 线性回归
给定数据集,习得
,使得
。
常见的是用均方误差最小化来进行性能度量。其几何意义是,使所有样本到直线(超平面)的欧式距离之和最小。
一般形式是,
对w求导得,
令其为0,可得w的最优解的闭式解。
1.1 满秩
或梯度下降求解,
1.2 L1正则化(Lasso回归)
当不是满秩,可以解出多个w,将通过算法的归纳偏好觉得最终的w。常见的做法是引入正则化(regularizaion)项(获得最优“稀疏性”的解)。
一般地,数据集D有n个属性,m个样本。令误差函数为(最小二乘法)
利用梯度下降求解,其中,
则
上式中,不论w>0或w<0,项都会使|w|更加接近0。
L1正则化,会使更多的权值等于0,所以可以产生稀疏模型(很多权值为0),进而用于特征选择。
1.3 L2正则化(Rridge回归)
误差函数为,
w偏导数为,
w更新公式为,
上式中,w每一次迭代都乘以了小于1的因子,使w能加速减小。总体来看w可以获得更小的值,从而防止过拟合。
L2正则化中,w等于0的几率小很多,所以不具有稀疏性
2. 广义线性回归
线性模型预测值逼近真实标记y时,就得到了线性回归模型。
令模型预测值逼近y的衍生物,如将输入标记的对数作为模型逼近的目标,。这就是“对数线性回归”,实际是让
,这已经是非线性函数映射了。
一般地,找一个单调可微函数将真实输出y与回归模型的预测值联系起来,单调可微函数,令
,称为“广义线性模型”。
2.1 Logistic回归
使用对数几率函数作为,得到
,即
。y视为样本x作为正例的可能性,1-y视为反例的可能性,两者比例称为“几率”,反应了x作为正例的相对可能性。所以称为对数几率函数。
通过“极大似然法”求解w,b:
将y视为概率估计,则
,显然有,
其对数似然函数为,
令,则
再令,则
或者
联立式(2.1),(2.2),(2.3),(2.4),最大化式(2.3)等价于最小化
偏导数为,
更新公式为,
3. 线性判别分析
LDA(Linear Discriminant Analysis)的思想是:设法将给定训练集的样例投影到一条直线上,使得同类样例的投影点尽可能接近,异类样例的投影点尽可能远离;对新样本进行分类时,将其投影到相同的直线,再根据投影点的位置确定样本类别。(组内方差小,组间方差大。)LDA 可从贝叶斯决策理论的角度来释,并可证明,当两类数据同先验、满足高斯分布且协方差相等时,LDA 可达到最优分类。
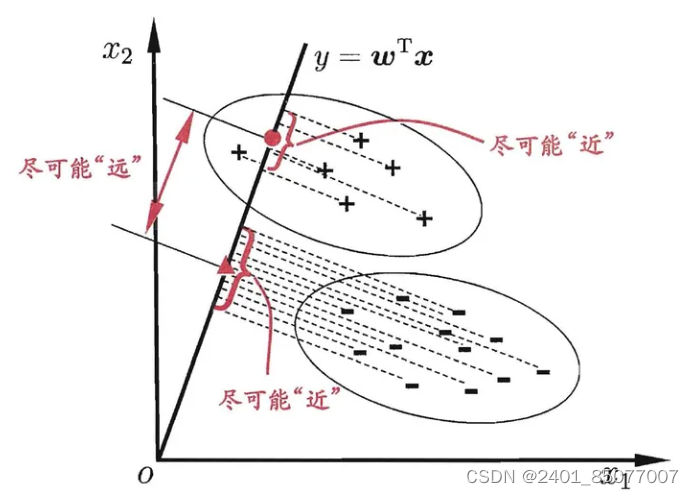
(w可以理解为这条过原点直线的方向的单位向量。点在直线的投影,则是向量的内积
,即x在w方向上的投影的长度,即x到远点的距离)
3.1 LDA二分类
考虑二分类问题,给定数据集,令
表示第i类样本的集合、均值向量、协方差矩阵。两类样本的中心点到直线的投影分别为
,
。
假设x属于第0类,则x的组内偏差为,其组内偏差之和为
,
,而
为方阵,将组内偏差相加的
就是其组内属性(特征)的协方差形式
。
所以欲使同类样本点的投影点接近,应使同类样本点的协方差尽可能小,即尽可能小;所以欲使异类样本点的投影点远离,应使中心点距离尽可能大,即
尽可能大。即最大化
定义“类内散度矩阵”,“类间散度矩阵”
,则
求解w:
J是关于w的二次项,因此解与w的长度无关,只与方向相关(所以直线也总是过原点的)。可令,则求解等价于
由拉格朗日乘子法得,
对w求偏导得,
令上式等于0,得,又w不关心大小,只关心方向,而
是一个标量,所以可得
(可以理解为w为矩阵
的特征值。
求逆时,考虑到数值稳定性,在实践中通常是对进行奇异值分解,即
。这里
是一个实对角矩阵,其对角线上的元素是
的奇异值,然后再由
得到
。)
3.2 LDA多分类
推广至多分类任务,设存在N个分类,表示第i类的样本数。
定义“全局散度矩阵”
类内散度矩阵
其中
化简求得
多分类LDA可以有多种实现方法:使用三者中的任何两个即可。
常见的一种实现是采用优化目标:
其中W是d×(N-1)的矩阵,d表示特征的维数,N表示类别数,tr(·)表示矩阵的迹。
与二分类同理,通过求解得,W的闭式解则是
的N-1个最大广义特征值所对应的特征向量组成的矩阵。
若将W 视为一个投影矩阵,则多分类LDA将样本投影到N−1维空间,N-1通常远小子数据原有的属性数。于是,可通过这个投影来减小样本点的维数,且投影过程中使用了类别信息,因此LDA也常被视为一种经典的监督降维技术。
4. 多分类问题
在多情形下,是基于一些基本策略,利用二分类学习器来解决多分类问题。
先将多分类任务拆解为多个二分类任务进行求解,针对每个二分类任务训练一个分类器;在测试时,再将这些分类器的预测结果进行集成以获得最终结果。关键就是任务如何拆分,结果如何集成。
分类策略“一对一”(OvO):
假设数据集,
。将N个类别两两配对,则得到N(N-1)/2个二分类任务。在测试时,将样本交给所有分类器,则得到N(N-1)/2个结果。最终结果可以通过投票得到,即把被预测得最多的类别作为最终分类结果。
分类策略“一对其余”(OvR):
每次将一个类别作为正例,其他类别作为反例得到N个分类器。在测试时,若仅有一个分类器预测为正例,则对应的类别为最终的结果;若有多个分类器预测为正例,则考虑各分类器的预测置信度,选择置信度最大的类别作为标记作为结果。例如:逻辑回归算,可将概率最高的那个模型对应的样本类型认为是该预测样本的类型。
(OvO需要训练N(N-1)/2个分类器,OvR需要训练N个分类器。所以OvO的存储和测试时间开销比OvR大。但在训练时,OvR每个分类器需要用到全部的样本,而OvO每个分类器只用两个类别的样本。所以当类别较多时,OvO的训练时间开销更小。)
分类策略“多对多”(MvM):
将一些类作为正例,剩余的作为反例。可以看出OvO和Ovr是MvM的特例。
纠错输出码技术(EROC):
第一步,编码(使用分类器对每个类别进行编码):对N个类别做M次划分,每次将一部分作为正例,其余作为反例。从而产生M个训练集,训练M个分类器。(每一个类别都会生成M个分类器形成的编码。)
第二部,解码:M个分类器分别对测试样本进行预测,将预测的标记组成一个编码,将编码和每个类别的编码进行比较,取距离最小的类别的作为最终结果。
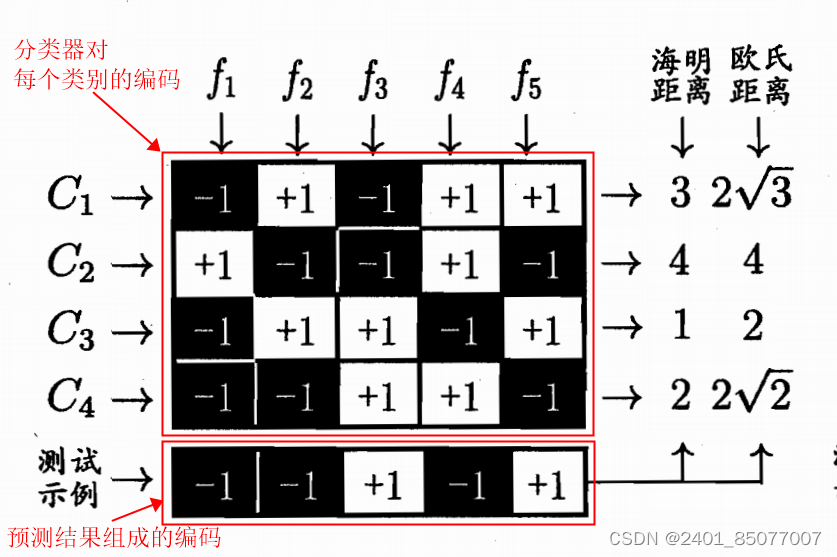
如何理解“纠错”:因为在测试阶段,ECOC 编码对分类器的错误有一定的容忍和修正能力。例如上图中,测试样本的正确预测编码是(-1,+1,+1,-1,+1)。但f2出错从而导致了错误编码(-1,-1,+1,-1,+1)。但基于这个编码仍能产生正确的最终分类结果 C3。
一般来说,对同一个学习任务,ECOC 编码越长,纠错能力越强。然而,编码越长,意味着所需训练的分类器越多,计算、存储开销都会增大;另一方面,对有限类别数,可能的组合数目是有限的,码长超过一定范围后就失去了意义。
5. 类别不平衡问题
在分类任务中,不同类别的训练样本数差别很大。
5.1 欠采样
去除一些反例,使正、反例数目接近,再进行学习。但随机丢弃可能丢弃重要的信息。代表算法是利用集成学习机制,将反例划分为若干个集合供不同模型学习。这样相当于对每个模型进行了欠采样,但全局没有丢失重要信息。
5.2 过采样
增加一些正例,使正、反例数目接近,再进行学习。不能简单地对初始正例进行重复采样,否则会导致严重的过拟合。代表算法有SMOTE,通过对训练集中的正例进行插值来产生额外的正例。
5.3 阈值移动
在线性分类器中,通常以预测的来判别为正例。几率
正例的可能性与反例的可能性的比值。分类器的决策规则为:
若,则为正例
但训练集中正、反例样本数不同时,记为正例的数目,
为反例的数目,则正例的观察几率为
。假设训练集是真实样本总体的无偏采样,即观察几率代表了真实几率。则分类器的决策规则为修正为:
若,则为正例
这就是“再缩放”。用
代替,就是代价敏感学习,
表示正例误判为反例的代价,
表示反例误判为正例的代价。
CONTINUE...





















 991
991











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








