结构化状态空间模型的直观解释（第二部分）

第 2 部分 - 面向图像、视频和时间序列的 Mamba 状态空间模型（欢迎来到雲闪世界。）

添加图片注释，不超过 140 字（可选）

年代状态空间模型几十年来为许多工程学科所熟知，现在在深度学习中首次亮相。在我们探索 Mamba 选择性状态空间模型及其最新研究成果的过程中，了解状态空间模型至关重要。而且，正如工程中经常出现的情况一样，正是细节让理论概念在实践中得以应用。除了状态空间模型之外，我们还必须讨论如何将它们应用于序列数据、如何处理长距离依赖关系以及如何通过利用某些矩阵结构来有效地训练它们。

结构化状态空间模型为 Mamba 构建了理论基础。然而，它们与系统理论和高级代数的联系可能是采用这一新框架的障碍之一。 因此，让我们分解一下，确保我们理解关键概念并将它们可视化，以阐明这一新旧理论。

即使您最终没有使用状态空间模型，了解一些技巧（例如为什么我们需要加速矩阵乘法以及如何利用某些矩阵结构来实现这一点）也肯定会提升您作为工程师或开发人员的技能。

在第 1 部分中，我们回顾了循环神经网络 (RNN) 和 Transformers 的优缺点，以说明为什么我们需要一种新的模型架构。 我们说 RNN 推理速度快，但训练速度慢，而 Transformer 训练速度快，但推理速度慢。 我们想要找到一个训练和推理速度都很快的模型，同时要与 Transformer 的性能相媲美。

2. 状态空间模型简介 Mamba 建立在通过学习各种矩阵将状态空间模型用于深度学习的理念之上。因此，在探索“结构化”部分的含义之前，让我们先简单了解一下状态空间模型。 状态空间模型可以定义为连续时间表示以处理连续信号，也可以离散化以处理离散数据序列。 我们最感兴趣的是离散状态空间模型，因为像循环神经网络 (RNN) 和 Transformers 一样，离散 SSM 处理数据序列，例如文本标记或模拟时间信号的样本。 2.1 状态空间模型的连续时间表示 连续时间状态空间模型描述了通过状态系统传播的输入信号与产生的输出信号之间的关系。

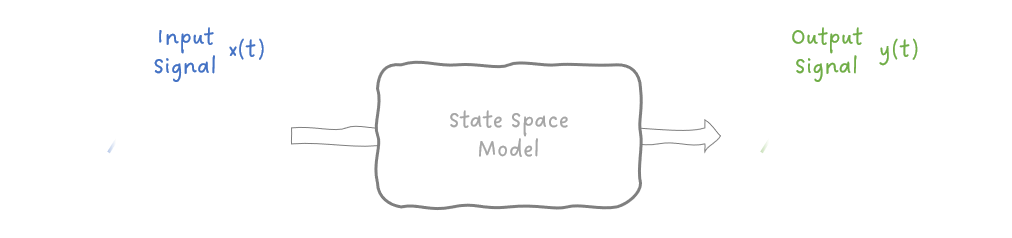
图 1：状态空间模型的高级功能。

这是从系统论中借用的一个思想。输出取决于输入和系统的当前状态，而当前状态取决于先前的状态和输入。 这种关系可以通过两个简单的方程有效地表述出来，其中A、B、C和D是矩阵（稍后我们会看到），x(t)是输入信号，y(t)是输出信号，h(t)和h'(t)分别是当前状态和更新状态。

方程 1：连续时间 SSM 的状态和输出方程。

矩阵D将输入x(t)进行变换，并将其映射到输出y(t)，这通常包含在经典 SSM 的输出方程中。 然而，当将 SSM 应用于深度学习时，我们会删除此变换并将其建模为简单的跳跃连接，从而简化 SSM。 我们可以用如下框图来表示这些方程：

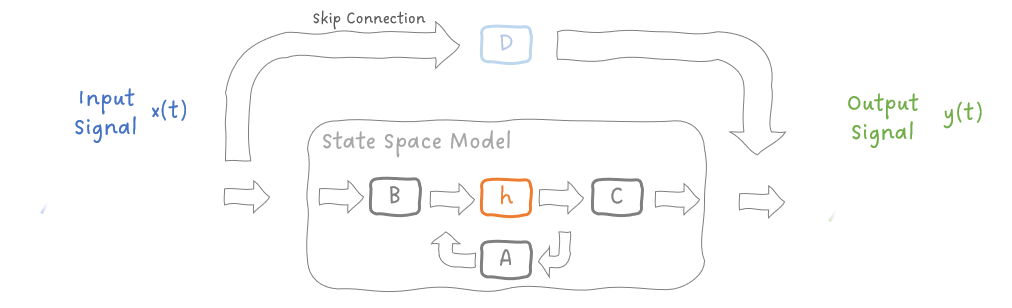
图 2：连续时间状态空间模型的框图

这是 SSM 的连续时间表示。但有两个困难：

1. 找到模型状态h(t)的解析解具有挑战性，并且

2. 因为我们使用计算机工作，所以我们通常处理离散信号，而不是连续信号。

2.2 状态空间模型的离散化 因此，我们实际上不是将函数x(t)映射到函数y(t)，而是将序列x[k]映射到序列y[k]。这意味着我们需要一个可以处理离散信号的离散状态空间模型。