促进银发经济发展政策下关于老龄化趋势的分析及其对市场与相关产业发展的影响
摘要
现代化中国人口变化重点体现在少子化、老龄化、人口负增长和区域人口增减分化等四个方面;与此同时,人口老龄化程度对市场经济的影响日益引起关注,同时国家近年来也越发注重银发经济先关产业的发展,因此本文以国家统计局1990年—2022年的人口普查数据和市场数据等为基础,在促进银发经济发展政策下分析人口老龄化程度和趋势以及其对相关产业发展的影响。
首先,进行人口数据的清洗和缺失值处理后,得到样本数据,然后借助SPSS软件运用ARIMA模型对人口数量变化趋势进行预测,再以人均国内生产总值和政府和社会卫生支出为自变量,老年人口系数为因变量建立VAR模型,直观的了解到未来人口老龄化程度进一步加剧的趋势。
其次,利用选取的变量指标通过岭回归分析,分别对因变量建立模型。发现人口的老龄化趋势对银发经济相关产业发展产生明显影响,特别是在医疗、保险等行业,同时也影响了我国的产业结构变化,对我国产业机构升级有促进作用。
最后,根据模型分析的结果得出对应结论:我国未来的人口数量可能出现下降趋势,老龄化程度也可能进一步加剧,同时老龄化程度的加剧对银发经济相关产业也会产生深远影响。
关键词:人口老龄化,银发经济,ARIMA,VAR,岭回归
目录
促进银发经济发展政策下关于老龄化趋势的分析及其对市场与相关产业发展的影响
表格和插图清单
图 1 基本研究思路
图 2 ARIMA模型基本程序
图 3 VAR模型基本程序
图 4 二阶差分序列图
图 5 年末总人口万模型拟合和预测
图 6 老龄化系数增量
图 7 老龄化系数
表1年末总人口数的ADF检验
表2 ARIMA(0,2,0)模型参数
表3模型Q统计量
表4预测值(13期)
表5模型检验
表6比重3-ADF检验
表7政府和社会卫生支出-ADF检验
表8社会服务机构数(个)-ADF检验
表9人均国内生产总值(元)-ADF检验
表10 Ln_政府和社会卫生支出-ADF检验
表11处理后的数据
表12 Johansen协整检验
表13定阶筛选
表14 VAR模型结果
表15模型预测
表16 2023—2035年老龄化相关数据
表17残差正态性检验
表 18岭回归
表19模型拟合
表20各产业不同年龄人口的标准系数
表21老龄化系数预测值
表22 二、三产业比值结果
一、研究背景及文献综述
(一)研究背景
2024年01月11日国务院办公厅印发《关于发展银发经济增进老年人福祉的意见》,这是国家出台的首个支持银发经济发展的专门文件【1】。在这份文件中解释了银发经济是指向老年人提供产品或服务,以及为老龄阶段做准备等一系列经济活动的总和。国家为何这么重视银发经济的发展呢?根本原因是我国日益加剧的人口老龄化程度【2】。截至2021年底,我国60岁及以上老年人口占总人数人口比例已达18.7%,老年人口规模位居世界首位。而根据新华社近日的解读,促进银发经济的发展一方面可以应对人口老龄化、实现人民对美好生活向往,另一方面,银发经济的发展涉及面广、产业链长、业态多元、潜力巨大。有望成为推动国内经济高质量发展的新支柱。因此为应对人口老龄化问题,并推动我国经济高质量发展,应当重视银发经济的发展问题。
(二)研究目的
人口老龄化趋势对银发经济相关产业的影响是深远且广泛的。随着人口老龄化的加剧,老年人口的数量和比例都在不断增长,这为银发经济相关产业带来了巨大的市场机遇和发展空间。鉴于银发经济发展局势所带来的新的机遇与挑战,探究未来的人口老龄化趋势并分析其对相关产业的影响,是银发经济高质量发展和应对人口老年龄化问题的重要前提。本文旨在分析中国未来的老龄化程度,以深一步了解发展银发经济的重要性;同时在此基础上研究老龄化对不同行业的影响程度,从而得出关于银发经济发展的进一步结论。最后,针对老龄化问题和银发经济发展提供一些建议,具有现实意义。
(三)文献综述
我国人口老龄化问题逐年加重,对我国社会经济发展产生了显著影响,国内学者针对人口老龄化问题产生的多方影响展开了研究。对于人口老龄化变化趋势的一类的问题,王争光等(2023)通过利用探索性空间分析等方法,探究了当地地区人口老龄化的变化特质;但又有王莹等(2015)通过建立Malthus模型,探究了人口老龄化的严重性。对于人口老龄化产生影响的一类问题,蔡昉(2024)通过分析探究人口负增长及老龄化所形成的银发经济将成为未来主流产业领域,阐述了银发经济对于未来中国社会发展的重要性【3】;同时有张翰文(2024)提出在人口老龄化日益严重的趋势下,发展“银发经济”是机遇也是一种挑战【4】;又有付云鹏等(2024)从其对就业质量的影响进行分析,利用多种模型探究人口老龄化对就业质量的影响。从内容上看,我国研究主要集中在人口未来变化趋势以及其对经济未来发展的影响,同时的在这些方面还有一些创新,但集合起来对人口趋势对有关“银发经济”发展的多方面影响的研究较少,本研究将在前人的研究成果上探究未来中国的人口老龄化到底是怎样的一个的趋势又会对那些产业产生极大影响。
二、介绍研究思路和模型
(一)主要研究思路
本文的主要研究思路是:选取相关指标先建立ARIMA模型预测人口未来变化趋势,带入国家统计局1990—2022年人口普查数据,预估未来十三年的人口数量变化。其次利用VAR模型,带入采集的国家统计局的数据,利用老龄人口系数作为人口老龄化程度的指标,并预测未来老龄化趋势变化情况。再在前两者基础上通过建立岭回归模型研究老龄化趋势下到底会对一些可能相关的行业产生怎样的影响,以及是否会影响到产业结构的变化。最后通过分析得出结论并提出相关意见和建议。

图 1基本研究思路
(二)模型介绍
1.ARIMA模型
ARIMA模型(Autoregressive Integrated Moving Average Model)即差分整合移动回归模型。ARIMA就是对非平稳时间序列进行d阶差分运算得到平稳序列,进而,对其通过AMRA(p,q)模型进行预测。其中p为自回归项,q为移动平均项数,d为时间序列成为平稳时所做的差分次数。利用自相关函数和偏自相关函数来确定p,q。 ARIMA模型的过程图表示如下:
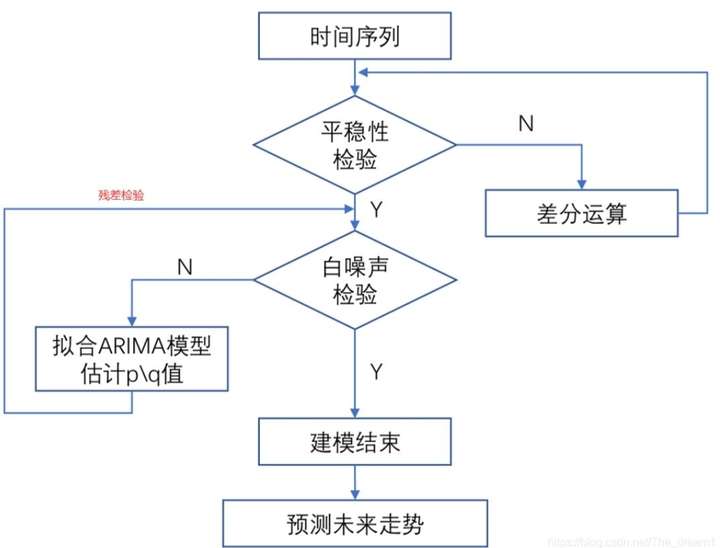
图 2 ARIMA模型基本程序
ARIMA模型在进行人口预测时,能很好的捕捉人口变化的动态性和复杂性,从而更准确地预测未来的人口趋势。因此本文选用ARIMA模型进行人口预测。
2.VAR模型
VAR模型称作向量自回归模型,是AR模型的向量形式。由Sims创立的一种经济统计模型,是非常重要,非常基础的统计模型。 VAR模型的流程图表示如下:

图 3 VAR模型基本程序
(本文主要通过VAR模型预测未来人口老龄化系数,而未着重分析各变量对其的动态影响,所以部分分析内容并未展示)
VAR模型常用语研究影响因素的问题,是一种短期动态影响研究即时变形特征(脉冲),可以处理多个变量之间的相关关系。该模型估计时,则无法避免无显著影响的变量或者滞后项。其次,在估计时要保证样本量足够大,使结果稳定。
3.岭回归模型
岭回归模型是一个不同于普通最小二乘的一个方法,当自变量间存在复共线关系,回归系数估计的方差就很大,估计值就很不稳定,这时就需要用到岭回归。岭回归(Ridge Regression,简记为RR)提出的想法是很自然的,当自变量间存在线性关系,普通最小二乘就不适用了,因为使用最小二乘必须要保证(XTX)Z这个矩阵是可逆的。
三、变量与数据说明
(一)变量的选取
本文首先对人口变化趋势做出预测并探究人口的老龄化趋势和其对劳动力市场、经济市场发展的相关影响,因此运用相关指标来衡量人口变化和老龄化趋势以及市场发展情况。本文的变量选取如下:
1.人口变化指标
本文选用1990—2022年末总人口数的数据作为衡量人口变化得指标,使用总人口数为指标一方面是因为其能直观明了的反应人口变化趋势,另一方面是因为其数据搜集也较为简便,数据不会出现缺失或异常情况,用其进行分析和建模的精确度更高。
2.人口老龄化指标
根据近年国家统计局的《人口老龄化及其衡量指标是什么》一文中的论述,以及其中提到的《人口学词典》中对人口老龄化的定义【5】,我们可以得出人口老龄化是指人口中老年人比重日益上升的现象【6】,尤其是指在已经达到老年状态的人口中,老年人口比重继续提高的过程。国际上通常用老年人口比重(本文选取65岁以上的人口占总人口的比重)作为衡量人口老龄化的标准,老年人口比重越高人口老龄化程度也越高。一般把60岁及以上的人口占总人口比重达到10%,或65岁及以上的人口占总人口的比重达到7%作为一个国家或地区进入老龄化社会(或老年型人口)的标准。虽然老化指数、少儿人口比例、老少比、年龄中位数等指标都可以在一定程度上反映人口老龄化的状况,但是老年人口比重是衡量人口老龄化最重要、最直观的一个指标,因此本文选取1990—2022的老年人口比重(老龄化系数)为被解释变量,通过对其的预测来衡量人口老龄化程度。
3.影响人口老龄化程度的相关指标
影响人口老龄化的直接因素为出生率与死亡率,但出生率与死亡率又受多个间接指标影响,本文参考相关文献,决定以人均国内生产总值、政府和社会的卫生费用支出以及社会服务机构数为相关指标探究其对老年人口系数的影响,进而预测人口老龄化程度。
4.与银发经济发展相关的指标
人口老龄化趋势对银发经济相关产业的影响是深远且广泛的。随着人口老龄化的加剧,老年人口的数量和比例都在不断增长,这为银发经济相关产业带来了巨大的市场机遇和发展空间。
首先,老年人口的增多直接推动了银发经济相关产业的快速发展。老年人群体的消费需求日益旺盛,对医疗保健、康复护理、养老服务等产业的需求不断增长。这促使了相关产业不断创新和升级,提供更加符合老年人需求的产品和服务。例如,医疗保健产业可以针对老年人的健康状况,提供定制化的健康管理方案;康复护理产业可以发展专业化的护理技术和设备,提高老年人的生活质量;养老服务产业可以完善养老服务体系,提供更加多样化、个性化的养老服务。
其次,人口老龄化趋势促进了银发经济相关产业链的完善和升级。随着老年人口对产品和服务的需求不断增长,相关产业链上下游的企业也将得到发展机会。例如,老年用品制造业可以研发更多适合老年人使用的产品,如助听器、助行器等;老年旅游产业可以开发适合老年人旅游的线路和服务,满足他们的休闲和娱乐需求。这些产业链的完善和升级将进一步推动银发经济的发展。
此外,银发经济对保险行业的影响同样显著。随着老年人口的增加和养老需求的扩大,养老金融产品的需求也将不断增长。保险作为养老金融的重要组成部分,将在银发经济中扮演重要角色。保险公司可以推出针对老年人的专属商业养老保险、商业医疗保险和商业长期护理保险等产品,以满足老年人的养老和医疗需求。同时,随着保险产品的不断创新和丰富,保险公司也将为老年人提供更加全面和个性化的保障服务。
因此本文经过推论分析,决定以卫生总费用(亿元)、社会保险基金收入(亿元)、第一产业增加值(亿元)、第二产业增加值(亿元)、第三产业增加值(亿元)、参加养老保险人数(万人))为反映银发经济发展的指标。
(二)数据来源
本文数据均来源于国家统计局和人口普查历年来的1990-2022的数据,数据较为权威和精准,部分数据存在缺失值情况,对缺失值的处理将在下节进行分析。
(三)缺失值的相关处理方法
本文在对数据进行搜集与统计时,对于社会服务机构数这种缺失值较少的数据,通常基于spss软件运用线性插值法对缺失数据进行替换,而社会服务机构数由于1990年数据缺失无法直接运用插值法,经过合理分析假设其为80000并运用线性插值法最终将1991和1992年的缺失值替换为84315和88631,并比较了缺失值替换过后的统计指标(如均值、方差等),确认替换效果良好,能反应原始数据的序列特征。而由于篇幅有限,本文对缺失值替换的详细过程不再进行进一步阐述。
四、实证分析
(一)人口数量变化预测—ARIMA模型
1.序列平稳性检验
针对年末总人口数据,先对它做序列图观察其平稳性,发现原序列与一阶差分后的序列均不平稳,二阶差分后序列较为平稳(如图4所示),为进一步研究序列的平稳性,对其进行ADF检验(如表1所示),发现该时间序列数据ADF检验的t统计量为3.243,p值为1.000,1%、5%、10%临界值分别为-3.770、-3.005、-2.643。p=1.000>0.1,不能拒绝原假设,序列不平稳。对序列进行一阶差分再进行ADF检验。一阶差分后数据ADF检验结果显示p=0.999>0.1,不能拒绝原假设,序列不平稳,对序列进行二阶差分再进行ADF检验。二阶差分后数据ADF检验结果显示p=0.000<0.01,有高于99%的把握拒绝原假设,此时序列平稳。

图 4 二阶差分序列图
表 1年末总人口数的ADF检验
| 差分阶数 | t | p | 临界值 | ||
|---|---|---|---|---|---|
| 1% | 5% | 10% | |||
| 0 | 3.243 | 1.000 | -3.770 | -3.005 | -2.643 |
| 1 | 2.372 | 0.999 | -3.788 | -3.013 | -2.646 |
| 2 | -5.907 | 0.000 | -3.670 | -2.964 | -2.621 |
2.模型的建立与检验
通过对年末总人口二阶差分序列图的观察和ADF检验,可知年末总人口的二阶差分数据基本满足平稳性序列的要求,则基于SPSS软件对年末总人口的二阶差分数据建立ARIMA模型,并对2022-2035年人口数据进行预测,针对年末总人口万人,结合AIC信息准则,对多个潜在备选模型进行建模和对比选择,最终找出最优模型为:ARMA(0,2,0),其模型公式为:y(t)=-50.806。 如下表:
表 2ARIMA(0,2,0)模型参数
| 项 | 符号 | 系数 | 标准误 | z 值 | p 值 | 95% CI |
|---|---|---|---|---|---|---|
| 常数项 | c | -50.806 | 21.681 | -2.343 | 0.019 | -93.299 ~ -8.313 |
| AIC值:386.414 | ||||||
| BIC值:389.282 |
ARIMA模型要求模型残差为白噪声,即残差不存在自相关性,可通过Q统计量检验进行白噪声检验(原假设:残差是白噪声)通过对模型Q统计量表格进行分析,Q6的p值大于0.1,则在0.1的显著性水平下不能拒绝原假设,模型的残差是白噪声,模型拟合效果良好,基本满足要求。表3展示模型Q统计量信息(具体为Ljung-Box Q检验统计量),包括统计量值和p值。
表 3模型Q统计量
| 项 | 统计量 | p 值 |
|---|---|---|
| Q1 | 0.403 | 0.526 |
| Q2 | 3.112 | 0.211 |
| Q3 | 3.295 | 0.348 |
| Q4 | 3.356 | 0.500 |
| Q5 | 4.772 | 0.444 |
| Q6 | 6.610 | 0.358 |
| Q7 | 6.637 | 0.468 |
| Q8 | 7.579 | 0.476 |
| Q9 | 8.416 | 0.493 |
| Q10 | 10.559 | 0.393 |
| Q11 | 10.867 | 0.455 |
| Q12 | 11.020 | 0.527 |
| Q13 | 12.150 | 0.515 |
| Q14 | 12.151 | 0.594 |
通过所得模型对2022-2035年的人口变化进行预测,结果如表4和图5所示:
表 4预测值(13期)
| 预测 | 值 | 均方根误差 | 均方误差MSE | 平均绝对误差MAE | 平均绝对百分比误差MAPE |
|---|---|---|---|---|---|
| 向后1期 | 141039.194 | 115.4731 | 13334.0271 | MAE: 84.6639 | 0.0006 |
| 向后2期 | 140852.581 | ||||
| 向后3期 | 140615.161 | ||||
| 向后4期 | 140326.935 | ||||
| 向后5期 | 139987.903 | ||||
| 向后6期 | 139598.065 | ||||
| 向后7期 | 139157.419 | ||||
| 向后8期 | 138665.968 | ||||
| 向后9期 | 138123.710 | ||||
| 向后10期 | 137530.645 | ||||
| 向后11期 | 136886.774 | ||||
| 向后12期 | 136192.097 | ||||
| 向后13期 | 135446.613 |

图 5 年末总人口万模型拟合和预测
拉格朗日乘数检验(Breush-Godfrey LM检验)用于检验模型残差序列是否存在序列相关。第一:LM检验原假设H0为序列不存在序列相关,备选假设H1为序列存在序列相关;第二:LM检验提供两个统计量分别是F和T * R方,通常使用F统计量。第三:对应p值大于0.05即接近原假设意味着序列不存在序列相关。 通过表5可知,F统计量的p值为0.688大于0.05,意味着残差序列不存在着自相关问题,所得模型具有优良的拟合度,能够很好的解释人口的变化趋势。
表 5模型检验
| 残差项LM检验 | |||
|---|---|---|---|
| F统计量 | 0.652 | p 值 | 0.688 |
| T *R2统计量 | 4.464 | p 值 | 0.614 |
3.人口变化影响分析
通过ARIMA模型对2022-2035年的预测结果可以看出,我国的未来总人口数很可能出现进一步下降趋势,而人口数量的持续下跌将会对我国的经济发展、社会服务体系 等方面产生长期而深远的影响,同时会进一步改变我国的社会结构,加剧人口老龄化问题。因而下文针对人口老龄化问题,对人口老龄化趋势进行预测。
(二)人口老龄化预测—VAR模型
1.序列的平稳性处理及协整检验
在时间序列进行预测时,通常情况下同一系统的几个研究变量之间均有着相互依存关系,因而为更好的利用各变量的此类关系,此时可以使用VAR模型(向量自回归模型)进行多变量预测。 本文基于SPSS软件,以老龄化系数(本文以比重3代指)、人均国内生产总值、政府和社会卫生支出以及社会服务机构数(个)为相关变量,运用VAR模型对人口老龄化趋势进行一定预测。 通常情况下,VAR模型需要满足单位根检验,如果没有单位根则直接构建VAR模型即可,如果研究变量有单位根,则说明不适合进行VAR模型构建,但是如果有单位根且满足同阶单整,此时说明VAR模型构建是适合的,与此同时研究变量满足协整关系也是一种常见的前提条件。因此我们先对序列进行单位根检验:
表 6比重3-ADF检验
| 差分阶数 | t | p | 临界值 | ||
|---|---|---|---|---|---|
| 1% | 5% | 10% | |||
| 0 | 8.453 | 1.000 | -3.654 | -2.957 | -2.618 |
| 1 | 0.252 | 0.975 | -3.679 | -2.968 | -2.623 |
| 2 | -5.982 | 0.000 | -3.679 | -2.968 | -2.623 |
表 7政府和社会卫生支出-ADF检验
| 差分阶数 | t | p | 临界值 | ||
|---|---|---|---|---|---|
| 1% | 5% | 10% | |||
| 0 | 0.705 | 0.990 | -3.770 | -3.005 | -2.643 |
| 1 | -0.198 | 0.939 | -3.788 | -3.013 | -2.646 |
| 2 | -1.776 | 0.393 | -3.788 | -3.013 | -2.646 |
表 8社会服务机构数(个)-ADF检验
| 差分阶数 | t | p | 临界值 | ||
|---|---|---|---|---|---|
| 1% | 5% | 10% | |||
| 0 | 3.419 | 1.000 | -3.654 | -2.957 | -2.618 |
| 1 | -3.364 | 0.012 | -3.661 | -2.961 | -2.619 |
表 9人均国内生产总值(元)-ADF检验
| 差分阶数 | t | p | 临界值 | ||
|---|---|---|---|---|---|
| 1% | 5% | 10% | |||
| 0 | 3.281 | 1.000 | -3.753 | -2.998 | -2.639 |
| 1 | 0.165 | 0.970 | -3.788 | -3.013 | -2.646 |
| 2 | -3.200 | 0.020 | -3.788 | -3.013 | -2.646 |
ADF检验验证时间序列是否平稳,其原假设为序列不平稳。一般p值小于0.1(也可以0.05为标准),即说明0.1水平下拒绝原假设,即序列平稳;(若序列不平稳,可进行一阶或二阶差分后,再进行ADF检验,直至序列平稳)。 由上表可见,比重3,政府和社会卫生支出,社会服务机构,人均国内生产总值均为非平稳序列,比重3,人均国内生产总值,均在二阶差分后达到平稳,即都为二阶单整,但社会服务机构数为一阶单整,且政府和社会卫生支出在二阶差分后仍为不平稳序列,由建立VAR模型的前提条件知,若原序列为非平稳序列则需满足同阶单整,且原序列间满足协整关系,方可建立VAR模型,因此我们需要对原数据进行处理使其满足同阶单整的条件。 首先,我们先来解决政府和社会卫生支出序列的不平稳问题,我们考虑对其做对数变换来减小数据的波动性,使得数据更加平稳,并且再对其进行单位根检验,则得到以下数据:
表 10Ln_政府和社会卫生支出-ADF检验
| 差分阶数 | t | p | 临界值 | ||
|---|---|---|---|---|---|
| 1% | 5% | 10% | |||
| 0 | -0.783 | 0.824 | -3.661 | -2.961 | -2.619 |
| 1 | -2.172 | 0.217 | -3.661 | -2.961 | -2.619 |
| 2 | -5.469 | 0.000 | -3.670 | -2.964 | -2.621 |
二阶差分后数据ADF检验结果显示p=0.000<0.01,有高于99%的把握拒绝原假设,此时序列平稳。则说明此时Ln_政府和社会卫生支出为二阶单整。 则以得,比重3,人均国内生产总值,Ln_政府和社会卫生支出为同阶单整,社会服务机构数为一阶单整,但VAR模型要求数据皆为同阶单整(或者有多个单整同阶的不同序列),此时还未满足条件,则我们应该对数据进行进一步处理。 我们此时考虑对比重3,人均国内生产总值,Ln_政府和社会卫生支出数据进行进一步差分处理,得到其增量设为新的解释变量,则其与社会服务机构数均为一阶同阶单整。即满足协整检验的前提。因此,我们对新的数据进行协整检验,以探究其是否可以建立VAR模型。
表 11处理后的数据
| 年份 | Ln_政府和社会卫生支出 | Diff1_人均国内生产总值(元) | Diff1_比重3 | Diff1_Ln_政府和社会卫生支出 | 社会服务机构数(个) |
|---|---|---|---|---|---|
| 1990年 | 6.174577457365838 | 80000 | |||
| 1991年 | 6.325182995532574 | 249 | 0.40000000000000036 | 0.150605538 | 84315 |
| 1992年 | 6.492482229882887 | 422 | 0.20000000000000018 | 0.16729923435031324 | 88631 |
| 1993年 | 6.6806162563924385 | 693 | 0 | 0.1881340265095517 | 92946 |
| 1994年 | 6.894862523440175 | 1054 | 0.20000000000000018 | 0.21424626704773608 | 98679 |
| 1995年 | 7.051985484653369 | 1010 | -0.20000000000000018 | 0.15712296121319458 | 115175 |
| 1996年 | 7.198385501366073 | 807 | 0.20000000000000018 | 0.14640001671270397 | 132309 |
| 1997年 | 7.31828752742332 | 583 | 0.09999999999999964 | 0.11990202605724676 | 134852 |
| 1998年 | 7.415229292371753 | 379 | 0.20000000000000018 | 0.09694176494843276 | 138366 |
| 1999年 | 7.48826553491348 | 369 | 0.20000000000000018 | 0.07303624254172725 | 146322 |
| 2000年 | 7.539803350174232 | 713 | 0.09999999999999964 | 0.05153781526075196 | 146341 |
| 2001年 | 7.606904411737717 | 775 | 0.09999999999999964 | 0.06710106156348505 | 152941 |
| 2002年 | 7.802981707982102 | 789 | 0.20000000000000018 | 0.1960772962443853 | 154196 |
| 2003年 | 7.974340120811487 | 1160 | 0.20000000000000018 | 0.17135841282938458 | 160007 |
| 2004年 | 8.16591224510896 | 1821 | 0.09999999999999964 | 0.1915721242974726 | 160352 |
| 2005年 | 8.328194995388527 | 1881 | 0.10000000000000053 | 0.16228275027956762 | 164962 |
| 2006年 | 8.5151470995973 | 2370 | 0.20000000000000018 | 0.18695210420877295 | 187888 |
| 2007年 | 8.775750217540775 | 3756 | 0.09999999999999964 | 0.2606031179434751 | 200162 |
| 2008年 | 9.066416882362772 | 3606 | 0.1999999999999993 | 0.29066666482199643 | 201758 |
| 2009年 | 9.302987919209391 | 2080 | 0.3000000000000007 | 0.23657103684661962 | 203275 |
| 2010年 | 9.467235863774878 | 4628 | 0.40000000000000036 | 0.16424794456548675 | 203945 |
| 2011年 | 9.672855406558273 | 5469 | 0.1999999999999993 | 0.20561954278339556 | 205926 |
| 2012年 | 9.823506676284323 | 3494 | 0.3000000000000007 | 0.15065126972604936 | 206743 |
| 2013年 | 9.949397382045326 | 3726 | 0.29999999999999893 | 0.12589070576100347 | 251939 |
| 2014年 | 10.08651677554194 | 3415 | 0.40000000000000036 | 0.13711939349661328 | 310652 |
| 2015年 | 10.27442988156406 | 3010 | 0.40000000000000036 | 0.18791310602212086 | 360956 |
| 2016年 | 10.404474636200131 | 3861 | 0.3000000000000007 | 0.1300447546360708 | 386186 |
| 2017年 | 10.531153901456715 | 5809 | 0.5999999999999996 | 0.12667926525658402 | 407453 |
| 2018年 | 10.65041030657811 | 5942 | 0.5 | 0.11925640512139424 | 426524 |
| 2019年 | 10.761460799106455 | 4544 | 0.6999999999999993 | 0.11105049252834576 | 510510 |
| 2020年 | 10.863136005257397 | 1750 | 0.9000000000000004 | 0.10167520615094183 | 527757 |
| 2021年 | 10.926645424539261 | 9542 | 0.6999999999999993 | 0.06350941928186415 | 567077 |
| 2022年 | 11.041105146543536 | 3940 | 0.7000000000000011 | 0.11445972200427512 | 587313 |
(diff代指差分)
表 12Johansen协整检验(迹统计量Trace)
| 原假设H0 | 特征根eigenvalue | 迹Trace | 10%临界值 | 5%临界值 | 1%临界值 |
|---|---|---|---|---|---|
| None(无协整关系) | 0.940 | 143.806 | 44.493 | 47.855 | 54.681 |
| 最多1个协整 | 0.786 | 64.885 | 27.067 | 29.796 | 35.463 |
| 最多2个协整 | 0.416 | 21.690 | 13.429 | 15.494 | 19.935 |
| 最多3个协整 | 0.210 | 6.615 | 2.705 | 3.841 | 6.635 |
上表格中,如果迹统计量的绝对值大于临界值的绝对值,则意味着显著,比如迹统计量的绝对值大于10%临界值绝对值则意味着10%水平显著,如果有呈现出显著性,则拒绝原假设。针对假设‘None(无协整关系)’:其迹统计量值为143.806,1%临界值为54.681,意味着1%水平上拒绝该假设。针对假设‘最多1个协整’:其迹统计量值为64.885,1%临界值为35.463,意味着1%水平上拒绝该假设。针对假设‘最多2个协整’:其迹统计量值为21.690,1%临界值为19.935,意味着1%水平上拒绝该假设。针对假设‘最多3个协整’:其迹统计量值为6.615,5%临界值为3.841,意味着5%水平上拒绝该假设。4个检验分别结论为至少1个协整,大于1个协整,大于2个协整关系,大于三个协整也即说明本案例中的四个研究变量之间均有着协整关系。
2.模型的建立与检验
因此由上述信息可知,所有变量为同阶单整,且满足协整关系,由此我们建立VAR模型,并对人口老龄化系数进行预测:
表 13定阶筛选
| 阶数 | AIC | BIC | FPE | HQIC |
|---|---|---|---|---|
| 0 | 24.916 | 25.110 | 66213851399.682 | 24.972 |
| 1 | 24.636 | 25.604 | 51008838537.517 | 24.915 |
| 2 | 24.212 | 25.954 | 36877175810.337 | 24.713 |
| 3 | 24.192 | 26.709 | 47638215225.707 | 24.917 |
| 4 | 22.466 | 25.756 | 15925919008.847 | 23.414 |
| 5 | 20.329* | 24.394* | 8226461235.794* | 21.500* |
| 备注:*代表该项下定阶阶数 |
从上表可以看出,AIC准则时应该以5阶为准, BIC准则时应该以5阶为准, FPE准则时应该以5阶为准, HQIC准则时应该以5阶为准。4个指标值中最小值为5阶,因而最终以5阶为准构建VAR模型。
表 14VAR模型结果
| Diff2_比重3 | |
|---|---|
| 常数 | -0.021(-1.052) |
| L1 Diff2_比重3 | -0.921(-1.861) |
| L1 Diff2_人均国内生产总值(元) | -0.000*(-2.032) |
| L1 Diff2_Ln_政府和社会卫生支出 | 0.520(1.359) |
| L1 Diff1_社会服务机构数(个) | 0.000(1.608) |
| L2 Diff2_比重3 | -0.423(-0.810) |
| L2 Diff2_人均国内生产总值(元) | 0.000(0.817) |
| L2 Diff2_Ln_政府和社会卫生支出 | -0.401(-0.897) |
| L2 Diff1_社会服务机构数(个) | -0.000**(-2.806) |
| L3 Diff2_比重3 | -0.175(-0.496) |
| L3 Diff2_人均国内生产总值(元) | 0.000*(2.118) |
| L3 Diff2_Ln_政府和社会卫生支出 | -0.784*(-2.378) |
| L3 Diff1_社会服务机构数(个) | 0.000**(3.561) |
| L4 Diff2_比重3 | -0.313(-1.482) |
| L4 Diff2_人均国内生产总值(元) | 0.000**(3.736) |
| L4 Diff2_Ln_政府和社会卫生支出 | 0.650(1.505) |
| L4 Diff1_社会服务机构数(个) | 0.000(0.935) |
| L5 Diff2_比重3 | -0.110(-0.738) |
| L5 Diff2_人均国内生产总值(元) | 0.000(0.141) |
| L5 Diff2_Ln_政府和社会卫生支出 | -0.462(-0.896) |
| L5 Diff1_社会服务机构数(个) | -0.000(-0.969) |
| nobs | 26 |
| llf | -327.851 |
| AIC值 | 31.681 |
| SC值 | 35.745 |
| HQIC值 | 32.851 |
| * p<0.05 ** p<0.01 括号里面为t 值 |
从上表格可知,VAR模型公式如下: 其中代表Diff2_比重3代表,代表L1.Diff2_比重3,代表L1.Diff2_人均国内生产总值(元),代表L1.Diff2_Ln_政府和社会卫生支出,代表L1.Diff1_社会服务机构数(个),L2.Diff2_比重3,代表L2.Diff2_人均国内生产总值(元),代表L2.Diff2_Ln_政府和社会卫生支出,代表L2.Diff1_社会服务机构数(个),代表L3.Diff2_比重3,代表L3.Diff2_人均国内生产总值(元),代表L3.Diff2_Ln_政府和社会卫生支出,代表L3.Diff1_社会服务机构数(个),代表L4.Diff2_比重3,代表L4.Diff2_人均国内生产总值(元),代表L4.Diff2_Ln_政府和社会卫生支出,代表L4.Diff1_社会服务机构数(个),代表L5.Diff2_比重3,代表L5.Diff2_人均国内生产总值(元),代表L5.Diff2_Ln_政府和社会卫生支出,代表L5.Diff1_社会服务机构数(个)。
表 15模型预测
| 预测 | Diff2_比重3 |
|---|---|
| 向后1期 | 0.500 |
| 向后2期 | -0.645 |
| 向后3期 | 1.079 |
| 向后4期 | -0.967 |
| 向后5期 | 0.803 |
| 向后6期 | -0.187 |
| 向后7期 | -0.271 |
| 向后8期 | 0.995 |
| 向后9期 | -0.983 |
| 向后10期 | 0.897 |
| 向后11期 | -0.558 |
得到差分的预测结果后,我们需要2023年和2024年的老龄化系数才能将其进行还原,但国家统计局只搜集了2023年的老龄化系数(为15.4%),因此我们只能得到人口老龄化系数2022-2035的增量,为了能更好的还原老龄系数的预测值,我们进行了多方面考虑并假设2024年的老龄化系数为16.0%,基于以上数据最终得出了2022-2035年的老龄化系数增量和22022-2035年老龄化系数的预测值(基于2024年为16.0%的假设),结果如图表所示:
表 16 2023—2035年老龄化相关数据
| 年份 | 老龄化系数 | 老龄化系数增量 |
|---|---|---|
| 2023年 | 15.4 | 0.5 |
| 2024年 | 16 | 0.6 |
| 2025年 | 17.1 | 1.1 |
| 2026年 | 17.5 | 0.4 |
| 2027年 | 19.1 | 1.6 |
| 2028年 | 19.6 | 0.5 |
| 2029年 | 21 | 1.4 |
| 2030年 | 22.2 | 1.2 |
| 2031年 | 23.1 | 0.9 |
| 2032年 | 25 | 1.9 |
| 2033年 | 26 | 1 |
| 2034年 | 27.8 | 1.8 |
| 2035年 | 29 | 1.2 |

图 6 老龄化系数增量

图 7 老龄化系数
下表格展示残差正态性检验结果;通常情况下,VAR模型需要满足残差正态性要求;原假设是满足正态性,如果拒绝原假设(p值小于0.05);则说明残差不满足正态性,反之说明残差满足正态性。从下表可知,残差序列接受原假设(p=0.381>0.05),即说明VAR模型残差满足正态性特质,模型的预测具有较高的可靠性和稳定性。
表 17残差正态性检验
| 原假设H0 | χ2值 | df 值 | p 值 | 5%临界值 |
|---|---|---|---|---|
| 残差序列正态分布 | 8.554 | 8 | 0.381 | 15.507 |
从上表可知,残差序列接受原假设(p=0.381>0.05),即说明VAR模型残差满足正态性特质,模型的预测具有较高的可靠性和稳定性。
3.老龄化趋势的影响分析
上文以老龄化系数、人均国内生产总值、政府和社会卫生支出、社会服务机构数为原始数据,并将数据进行了差分和对数变换等先关处理,再通过VAR模型进行建模,对2023—2035的老龄化系数进行了预测。从预测结果可以看出我国的人口老龄化程度有进一步加深趋势,在2035年左右,老龄化系甚至数可能会接近30%,因此无论从何种角度来说,人口老龄化问题都是我国需要长期重视的问题,因此重视银发经济的发展潜能和前景是结合我国国情和现状所得出的必然结论。下文将结合人口老龄化数据对银发经济相关发展进行探讨。
(三)老龄化对银发经济相关产业发展的影响—岭回归模型
1.变量说明
本文将以0至14岁人口(万人)、15至64岁人口(万人)、65岁及以上人口(万人)为自变量,卫生总费用(亿元)、社会保险基金收入(亿元)、参加养老保险人数(万人)、第一产业增加值(亿元)、第二产业增加值(亿元)、第三产业增加值(亿元)、为因变量,通过岭回归分析,分别对因变量建立模型,以探究不同年龄段群体对银发经济相关产业的影响,以及对产业结构变化的影响。
2.结合岭迹图确认K值
将@0至14岁人口(万人),@15至64岁人口(万人),@65岁及以上人口(万人)作为自变量,分别将卫生总费用(亿元)等六个作为因变量进行Ridge回归(岭回归)分析后得到岭迹图,通过岭迹图查看确定最佳K值皆为0.02。
3.确定k值后建立模型
得到模型公式有:
卫生总费用(亿元)=29910.070-0.653*@0至14岁人口-0.731*@15至64岁人口 + 6.752*@65岁及以上人口
社会保险基金收入(亿元)=45884.139-0.825*@0至14岁人口-1.053*@15至64岁人口 + 8.565*@65岁及以上人口
参加养老保险人数(万人)=5967.786-0.580*@0至14岁人口 + 0.011*@15至64岁人口 + 2.783*@65岁及以上人口
第一产业增加值(亿元)=20460.121-1.258*@0至14岁人口-0.154*@15至64岁人口+ 5.386*@65岁及以上人口。
第二产业增加值(亿元)=321675.318-10.523*@0至14岁人口-2.523*@15至64岁人口 + 30.984*@65岁及以上人口。
第三产业增加值(亿元)=247721.213-7.294*@0至14岁人口-4.802*@15至64岁人口 + 50.461*@65岁及以上人口。
表 18岭回归
| 因变量 | 卫生总费用(亿元) | 社会保险基金收入(亿元) | 参加养老保险人数(万人) | 第一产业增加值(亿元) | 第二产业增加值(亿元) | 第三产业增加值(亿元) |
|---|---|---|---|---|---|---|
| 标准化系数 | ||||||
| Beta | ||||||
| 常数 | - | - | - | - | - | - |
| @0至14岁人口 | -0.099 | -0.100 | -0.167 | -0.192 | -0.280 | -0.140 |
| @15至64岁人 | -0.242 | -0.278 | 0.007 | -0.051 | -0.147 | -0.201 |
| @65岁及以上人口 | 1.073 | 1.088 | 0.840 | 0.863 | 0.867 | 1.014 |
表 19模型拟合
| 样本量 | 因变量 | R 2 | 调整R 2 | 模型误差RMSE |
|---|---|---|---|---|
| 33 | 卫生总费用(亿元) | 0.991 | 0.990 | 2411.475 |
| 33 | 社会保险基金收入(亿元) | 0.975 | 0.973 | 4914.368 |
| 33 | 参加养老保险人数(万人) | 0.989 | 0.988 | 1389.958 |
| 33 | 第一产业增加值(亿元) | 0.984 | 0.983 | 3103.758 |
| 33 | 第二产业增加值(亿元) | 0.986 | 0.985 | 16751.289 |
| 33 | 第三产业增加值(亿元) | 0.986 | 0.984 | 23600.162 |
上表可见所以模型R方均在0.95以上,说明模型的拟合度较高,解释力较强。
4.模型的分析与应用
根据上述模型,我们首先可以看出卫生总费用与65岁及以上人口呈现出正相关关系,而与其他人口数量均呈现负相关关系,且影响程度远大于另外两项,则可以反应出随着老龄人口数和老龄化趋势的增加,将极大的增多我国在医疗和卫生方面的支出,对于医疗卫生事业发展有着促进作用。
再分析其对保险相关行业的影响,对于社会保险基金收入来说,老年人口数的系数为正,且标准系数甚至大于卫生总费用时的标准系数,说明其对社会保险基金收入影响还要大,再结合参加养老保险人数来看,虽然15至64岁人口和65岁及以上人口皆对其呈正相关影响,但后者的标准化系数明显远大于后者,说明参加养老保险人数主要还是受到65岁及以上人口的影响,综上所述人口老龄化对促进我国相关的养老保险等保险业的发展有着高度影响。
最后我们来观察各产业的增值和产业结构是如何受到老龄化趋势的影响,通过观察各产业不同年龄人口的标准系数可见,65岁及以上人口依然在其中起着最大且呈正相关的影响,各产业其对应的标准系数分别为0.863、0.867、1.014,从中可见老龄人口对第三产业的影响是最大的,这正好反应了第三产业相关的服务业、医疗和保险行业等,将会是未来银发经济发展的重点关注行业。
表 20各产业不同年龄人口的标准系数
| 时间 | 预测值 | 真实值 | ||||
|---|---|---|---|---|---|---|
| 第一产业增加值(亿元) | 第二产业增加值(亿元) | 第三产业增加值(亿元) | 第一产业增加值(亿元) | 第二产业增加值(亿元 | 第三产业增加值(亿元) | |
| 2021年 | 82578.3 | 439910.2 | 616272.5 | 83216.5 | 451544.1 | 614476.4 |
| 2022年 | 88549.1 | 477178.1 | 669551.1 | 88207 | 473789.9 | 642727.1 |
从上表可以看出,模型在2021年、2022年的预测值都极其接近于真实值,说明该模型可以较好的模拟各产业的增加值变化,为了更好的体现人口老龄化对各产业的影响,结合上文对人口及老龄化趋势的预测,我们分别假定在总人口大致不变的情况下,当未来老龄化系数达到20%和25%时,通过模型模拟出各产业的生产总值。如表所示:
表 21老龄化系数预测值
| 老龄化系数 | 预测值 | ||
|---|---|---|---|
| 第一产业增加值(亿元) | 第二产业增加值(亿元) | 第三产业增加值(亿元) | |
| 20% | 132780.8 | 749533.7 | 1079683.7 |
| 25% | 175781.7 | 1014286.1 | 1478560.7 |
可见我国未来随着时代发展和人口老龄化程度的加剧,各产业增加值均有上升,但第三产业的增加值明显大于一、二产业的增加值,其中以第三产业为最高,第二产业次之,第一产业的增加量则远远小于二、三产业。我们同时用2021、2022年以及老龄化系数为20%和25%的产业增加量值,将后一个产业与前一个产业的增加量做比(分比记作比值1,比值2),更加详细直观的体现产业结构的变化。结果如下表所示:
表 22二、三产业比值结果
| 年份或老龄化系数 | 后一个产业增加值/前一个产业增加值 | |
|---|---|---|
| 比值1 | 比值2 | |
| 2021 | 5.4 | 1.36 |
| 2022 | 5.37 | 1.35 |
| 20% | 5.60 | 1.44 |
| 25% | 5.77 | 1.45 |
通过对表的观察,可以看出我国的二三产业所占比例大致将随着老龄化趋势出现上升,也可以说明随着时代发展和老龄化加剧,我国的产业结构将进一步向着二、三产业发展升级,特别是以第三产业为重以应对人口老龄化趋势下面对的问题与挑战。
五、总结与建议
本文基于人口老龄化影响经济发展事实,首先利用ARIMA模型进行了预测,观察了人口数量变化趋势。此外还利用向量自回归模型预测了未来人口老龄化变化趋势。再用岭回归模型分析了老龄化趋势下,医疗、保险行业以及产业结构可能受到的影响。因而得到以下结论:我国未来总人口数可能出现进一步下跌,老龄化程度将更为严重,老龄化趋势的增加,将极大的增多我国在医疗和卫生方面的支出,对于医疗卫生事业发展有着促进作用,对保险相关产业也有着高度影响,同时人口的老龄化也将对产业结构产生极大冲击,特别是第三产业的发展状况,在银发经济发展的新政策下,需要给予更多的重视和关注。
针对上述结论,为推动国内经济高质量发展,有效处理人口老龄化问题,本文提出以下建议:
-
为应对未来人口老龄化趋势,需加强对老龄劳动人群的综合素质培养。在老龄化趋势无可避免的情况下,为了防止发生劳动力锐减等情况,政府需要提升老龄劳动人群的专业化水平和综合竞争力。
-
为处理老龄化问题,在人口变化而导致经济缺口的情况下,需紧抓银发经济的相关产业发展来填补经济增长缺口,从而破除老龄化带来的不利情况,使得供给和需求相互促进。
-
为促进银发经济的发展,需要着重关注医疗、保险以及第三产业的发展状况,特别是与养老相关的医疗、保险以及服务业,在未来具有着巨大潜力。
六、创新与不足
(一)创新
本文研究促进银发经济发展政策下关于老龄化趋势的分析及其对市场与相关产业发展的影响,选题新颖,特别是在通过岭回归分析探究不同年龄段群体对银发经济相关产业的影响及对产业结构变化的影响时,基于上文对人口数量变化的预测以及对未来老龄化程度的判断,从而利用未来人口虽出现下降却大致稳定的条件,结合对老龄化的分析,在假定老龄化程度达到20%及25%的条件下,对未来的各产业增加值进行了预测,从而进一步观察出在老龄化程度加剧的情况下,我国产业结构可能的变化趋势。
(二)不足
本文在进行VAR建模以预测老龄化趋势时,所得模型的残差序列存在自相关性,意味着可能存在遗漏变量而对预测的准确性产生影响,同时本文在分析预测中经过分析做出过少量假设,以便进行更好的预测,例如在岭回归分析中假定未来人口大致不变,但是通过预测人口变化,未来人口数还是可能出现一定下降趋势的,因此通过假定计算出来的结果可能在精度方面会受到一定影响。
参考文献
-
国务院办公厅关于发展银发经济增进老年人福祉的意见,2024-01-15.
-
2024年国办一号文,聚焦银发经济,2024-01-17.
-
蔡昉.银发经济与银发经济学[J].新金融,2024,(04):4-7.
-
张瀚文.化老龄人口短板为跳板“银发经济”可成为新的经济增长点[N].河南商报,2024-04-30(A06).
-
领导干部统计知识问答:人口老龄化及其老龄化的标准是什么,2023-01-01.
-
人口词学典.
附录
本文提到的简称与全称对应表:
| 老年人口比重 | 老龄化系数 | 比重3 |
|---|---|---|
| 各年龄人口数 | @各年龄人口数 |
统计软件:SPSS26.0,SPSSAU



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








