初值定理-2025考研良哥信号与系统复习大全

 

信号与系统考研必备：Z变换基本性质与初值定理深度解析

在信号与系统的考研征途中，Z变换及其基本性质是我们无法绕过的知识点。而其中的初值定理，更是解题时的一把利器。今天，我们就来一起深入探讨Z变换的基本性质，并重点解析初值定理，为你的考研复习增添一份助力！

🔍 Z变换基本性质概览

Z变换，作为离散时间信号分析的重要工具，其基本性质众多且应用广泛。这些性质包括但不限于线性性质、时移性质、频移性质、尺度变换性质以及我们今天要重点讨论的初值定理。掌握这些性质，对于理解和分析离散时间信号具有重要意义。

🌟 初值定理详解

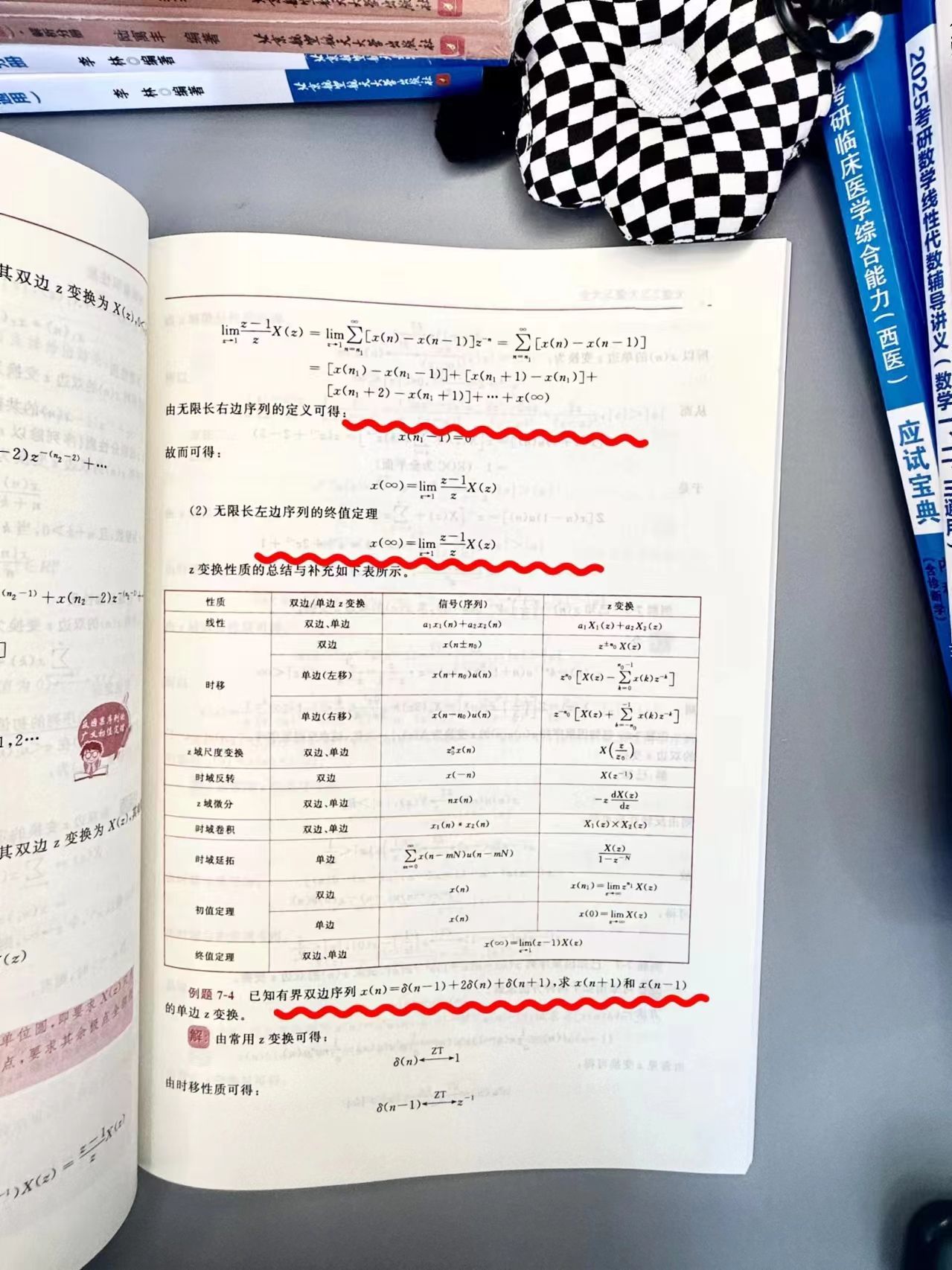
📚 定义与公式

初值定理是Z变换中的一个重要定理，它给出了在特定条件下，离散时间信号的初始值与其Z变换在z=1处的极限值之间的关系。具体地，若离散时间信号x[n]满足一定条件（如绝对可和或因果等），则其初值x[0]可由Z变换X(z)在z=1处的极限求得，即：

x[0]=z→1lim(z−1)X(z)

注意，这里的条件“z=1处的极限存在”是关键，它要求X(z)在z=1附近是解析的，且没有极点或零点恰好位于z=1。

🌈 理解与应用

初值定理的实质是通过Z变换在复平面上的一个特定点（z=1）来求解信号的初始值。这种方法的优点在于，它避免了直接对信号进行复杂的时域分析，而是利用Z变换的频域特性来间接求解。因此，在处理一些复杂的离散时间信号时，初值定理显得尤为有用。

🌰 实例解析

假设我们有一个简单的离散时间信号x[n]=anu[n]（其中∣a∣<1，u[n]为单位阶跃函数），其Z变换为X(z)=1−az−11。现在，我们想要利用初值定理来求解信号的初始值x[0]。

首先，我们注意到信号是因果的，且∣a∣<1保证了Z变换在z=1处是收敛的。然后，我们计算(z−1)X(z)在z=1处的极限：

#考研[话题]#&nbsp; #考研信号与系统[话题]#&nbsp;&nbsp; #考研良哥[话题]#&nbsp;&nbsp; #考研信号与系统网课[话题]#&nbsp; #2025考研[话题]#&nbsp; #复习大全[话题]#&nbsp; #研究生初试[话题]#&nbsp; #北京邮电大学考研[话题]#