初值定理-考研信号与系统复习大全

信号与系统考研秘籍：Z变换基本性质之初值定理深度解析

在信号与系统考研的征途中，Z变换作为连接离散时间信号与系统的重要工具，其基本性质是我们必须熟练掌握的。今天，我们就来聚焦Z变换的一个关键性质——初值定理，帮助大家更好地理解和应用这一重要概念。

🔍 Z变换的基本性质概览

Z变换作为离散时间信号的频域表示方法，具有一系列独特的性质，如线性性、时移性、尺度变换性等。这些性质不仅丰富了信号与系统分析的手段，也为解题提供了强有力的工具。而初值定理，则是这些性质中尤为重要的一个。

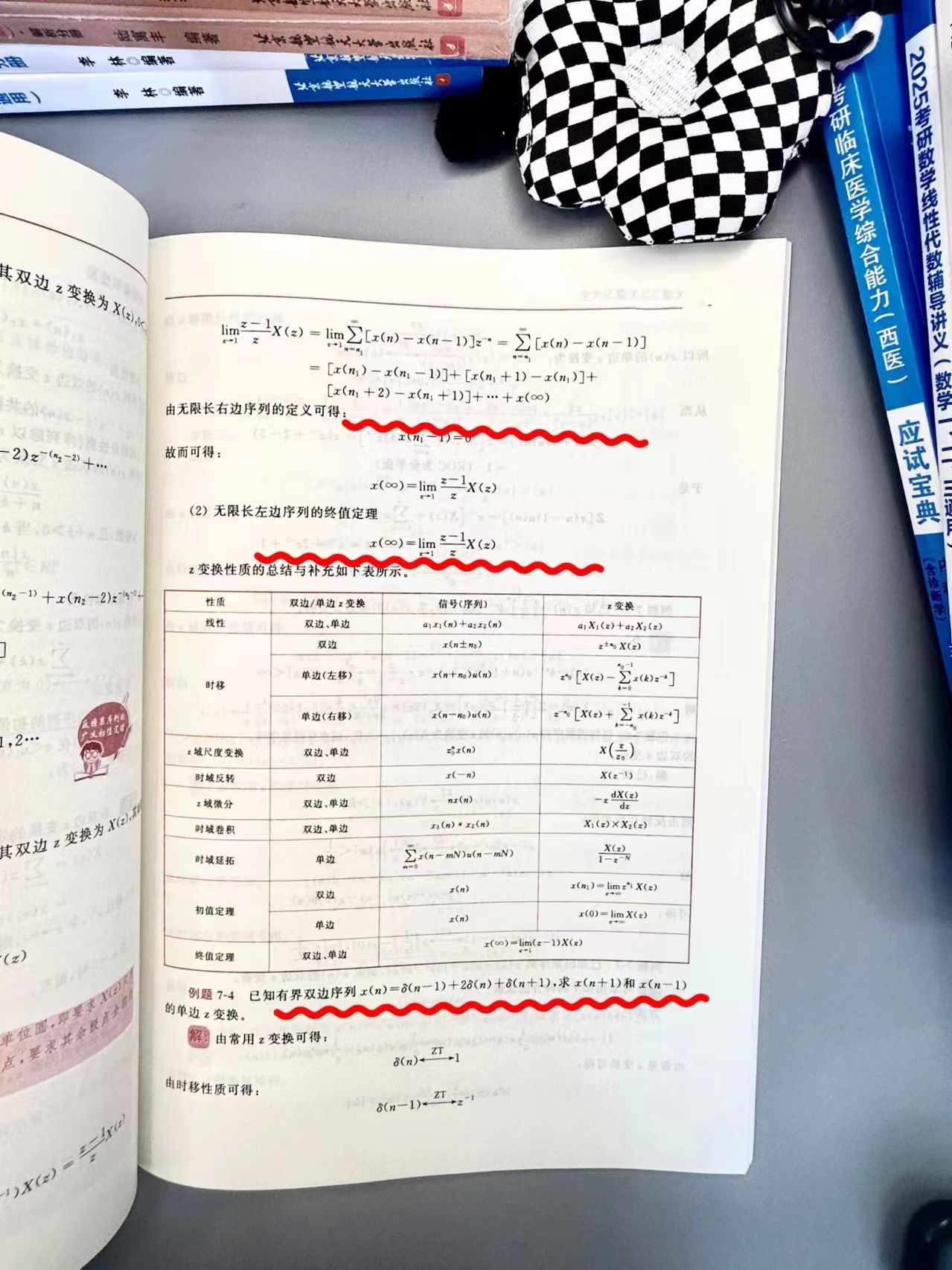
📝 初值定理是什么？

初值定理，简单来说，就是通过Z变换在z=1处的极限值（如果存在）来直接求取离散时间信号在n=0时刻的值。这一性质在求解系统初始响应时尤为有用，能够大大简化计算过程。

🔍 初值定理的数学表达

如果离散时间信号x[n]的Z变换X(z)在z=1处存在极限，即limz→1(z−1)X(z)=M存在且有限，则根据初值定理，信号在n=0时刻的值x[0]可以由下式给出：

[
x[0] = \lim_{{z \to 1}} (z-1)X(z) = M
]

📝 初值定理的应用场景

初值定理在信号与系统分析中有着广泛的应用。例如，在求解线性时不变（LTI）离散时间系统的初始响应时，如果已知系统的单位脉冲响应h[n]的Z变换H(z)，并且满足初值定理的条件，那么我们就可以直接利用初值定理求出系统在特定输入下的初始输出值。

💡 复习小贴士

1. 理解原理：深入理解初值定理的数学原理和物理意义，明确其适用条件和限制。
2. 熟练掌握：通过大量练习熟练掌握初值定理的应用方法，提高解题速度和准确性。
3. 结合系统分析：将初值定理与系统分析相结合，理解其在系统响应求解中的重要作用。
4. 注意细节：在应用初值定理时，要注意检查Z变换在z=1处的极限是否存在且有限，以避免错误。

📚 总结

初值定理作为Z变换的一个重要性质，在信号与系统考研复习中占据着重要地位。通过深入理解和熟练掌握这一性质，我们可以更加高效地解决相关考题，为考研之路增添一份信心。希望这篇笔记能够帮助大家更好地理解和应用初值定理，祝大家在考研中取得优异成绩！🌟#考研[话题]# #考研信号与系统[话题]# #考研良哥[话题]# #考研信号与系统网课[话题]# #2025考研[话题]# #复习大全[话题]# #研究生初试[话题]# #北京邮电大学考研[话题]#