机器学习(4-1)：神经网络(Neural Network)之一：基本概念-CSDN博客

本文链接：https://blog.csdn.net/2401_86889724/article/details/148040547

神经网络实际上是一个相对古老的算法，因为以前的算力不行，沉寂了一段时间，不过到了现在它又成为许多机器学习问题的首选技术。

4.1.1 神经网络产生的背景

之前我们已经介绍过线性回归（可以实现复杂曲线模拟）和逻辑回归（可以实现多分类）算法了，似乎可以解决较复杂的问题，那为什么还要研究神经网络？

这是因为：

1、即便只有两个输入特征 $x{_{1}}$ $_{}$ 、 $x{_{2}}$ 时，对于复杂的情况，我们可能需要如下的比较复杂的假设函数：

然而对于许多复杂的机器学习问题而言，涉及的输入特征往往多于两个。这样就造成了假设函数变得异常复杂。

2、对于图像处理，每个图像的像素多少就是其输入特征，对于50x50的图像而言，其输入特征就是2500个，若是更大的图像，其输入特征的个数将变得非常多！

对于输入特征过多的问题，线性回归、逻辑回归面临的计算量过大，所以需要一种新的算法。

对于逻辑回归而言，

为了阐述研究神经网络算法的目的，我们首先来看几个机器学习问题作为例子。这几个问题的解决都依赖于复杂的非线性分类器。

4.1.2 神经元模型

上图中，黄色的圆圈就代表了一个神经元，

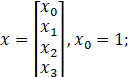为输入向量，代表神经元的权重（实际上就是我们之前所说的模型参数），代表激励函数（在神经网络术语中，激励函数只是对类似非线性函数的另一个术语称呼，）。

记为单个神经元的输出，又称单个神经元的激活项。

实际上，你可以这样理解，神经元就是权重。

当将输入送进神经元后，经计算（实际上就是）会有一个输出，这个输出再送入激励函数中，便得到了神经元的真实输出。

注意：当我们绘制一个神经网络时，当我绘制一个神经网络时，通常我只绘制输入节点等等，但有时也可以增加一个额外的节点，这个节点有时也被称作偏置单位或偏置神经元。但因为总是等于1，所以有时候，我们会画出它，有时我们不会画出，这要看画出它是否对例子有利。

4.1.3 最简单的三层神经元网络

上面介绍了单个神经元。神经元网络就是神经元连在一起的集合，如下图：

神经网络就是不同的神经元组合在一起。第一层为输入层，最后一层为输出层，而中间的所有层均为隐藏层。

注意：

输入单元，再说一次，有时也可以画上额外的节点。
同时，这里有3个神经元，记为，然后像输入单元一样，我们可以在这里添加一个，这和一样，代表一个额外的偏度单元，它的值永远是1（注意：中计算的是的值，而)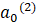 中存放的就是偏置1）。

为了能理解神经元网络中的计算，我们还要讲几个概念。

由于有3个神经元，其激活项为，与四个输入项（含一个偏置项 ）进行网状连接。

对于第一个神经元的激活项，其对应于输入项的权重记为，则有：

同理，有：

记，令，记，则有：

推而广之，定义：

1、向量是神经元在层的激活项，激活项是指神经元经计算后的输出。

2、矩阵称为权重矩阵，神经网络被该矩阵参数化，该矩阵其控制从第层到第层的映射。

如果一个网络在第 层有 个单元，在层有 个单元，那么矩阵，

总之，以上我们的这样一张图，展示了是怎样定义一个人工神经网络的。这个神经网络定义了函数：从输入到输出的映射。我将这些假设的参数，这样一来不同的，对应了不同的假设，所以我们有不同的函数，比如说从到的映射。

前向传播

在前面3个神经元构成的1个输入层、1个隐藏层，1个输出层神经网络中，有：

设 ，则有：

设，，则有：

再设，则有：

增加，则有：

以上是计算的过程，这个过程叫做前向传播。这个命名的含义是我们从输入层开始，向前传给第一层隐藏层，然后继续前向传播，直到最后的输出层。

神经网络与逻辑回归

我们观察上图，如果把输入层遮罩，则有

看起来像逻辑回归。即

这实际上就是一个标准的逻辑回归，只不过是输入特征值是隐藏层的激活项而已。

有趣的是，激活项是通过学习得到的函数输入值，也就是第一层到第二层之间的 ，而不是由训练输入项 ，得到的，而是自己训练逻辑回归得到的输入项的权重矩阵。

4.1.4 神经网络实现与(AND)、或(OR)、非(NOT)

与（AND)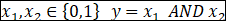

现在来看看神经网络是如何实现与门的。

我们增加一个单元，给三个单元分别赋予权重-30、+20、+20。则有

我们已知的图像如下：当，当


0	0	g-30≈0
0	1	g-10≈0
1	0	g-10≈0
1	1	g+10≈1

这样神经元就实现了与门(AND)。

或(OR)

我们增加一个单元x0=1 ，给三个单元分别赋予权重-10、+20、+20。则有


0	0	g-10≈0
0	1	g+10≈1
1	0	g+10≈1
1	1	g+30≈1

这样神经元就实现了或门(OR)。

非(NOT)

我们增加一个单元，给两个单元分别赋予权重10、-20。则有

	x
0
1

这样神经元就实现了非门(NOT)。

当然，我们还可以实现与非门、或非门、异或门，这里就不再列举了。

4.1.5 多元分类

对于一张输入图片，需要识别其属于行人、轿车、摩托车或者卡车中的一个类型，就是一个多元分类的问题。

神经网络模型也可以处理多分类任务。与二分类不同的是，多分类模型最后的输出层将是一个K维的向量，K表示类别数。用神经网络表示如下：

可以说，神经网络就是由一个个逻辑回归模型连接而成的，它们彼此作为输入和输出。输出结果可表示为：

训练集为：

当时，表示识别的是行人

当时，表示识别的是汽车

当时，表示识别的是摩托车

当时，表示识别的是卡车

用0与1的组合成的向量代替1，2，3，4：则有：

神经网络比直接使用Logistic回归的优势在于：

如果给定基础特征的数量为100，那么在利用Logistic回归解决复杂分类问题时会遇到特征项爆炸增长，造成过拟合以及运算量过大问题。

而对于神经网络，可以通过隐藏层数量和隐藏单元数量来控制假设函数的复杂程度，并且在计算时只计算一次项特征变量。其实本质上来说，神经网络是通过这样一个网络结构隐含地找到了所需要的高次特征项，从而化简了繁重的计算。

4.1.6 对神经网络的理解

对神经网络更直观的理解就是，它通过大量的隐藏层网络将输入向量进行一步又一步的抽象（加权求和+非线性变换），生成能够更加容易解释模型的复杂新特征，最后将这些强大的新特征传入输出层获得预测结果。就像单层神经元（无隐藏层）无法表示逻辑同或运算，但是若加上一个隐藏层结构就可以轻松表示出逻辑同或运算！